位图¶

约 2895 个字 137 行代码 10 张图片预计阅读时间 11 分钟

案例引入¶

给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在这40亿个数中。

Note

本题为腾讯/百度等公司出过的一个面试题

思路1：暴力遍历，时间复杂度\(O(N)\)，太慢
思路2：排序+二分查找，时间复杂度消耗\(O(Nlog_{2}{N}) + O(log_{2}{N})\)

Note

思路2在理论上可行的原因：

首先在消耗时间上，尽管排序的时间复杂度是\(O(Nlog_{2}{N})\)，但是排序只会进行依次，之后的时间消耗都只是二分查找上的消耗，而对40亿取2的对数可以得出差不多需要32次左右的次数，推导如下：

\(2^{10} = 1024\)

\(2^{20} = 1024 \times 1024 = 1,048,576\) (一百万)

\(2^{30} = 1024 \times 1024 \times 1024 = 1073741824\)（十亿）

则有40亿：

\(2^2 \times 2^{30} = 2^{32} = 4 \times 2^{30} = 4,294,967,296\)（四十亿）

深入分析解题思路2是否可行，可以先算算40亿个数据大概需要多少内存：

因为题目说的是无符号整数，在C语言/C++中，一个整数占用4个字节，40亿个数据就占用\(4 \times 40\)亿个字节，因为\(1 GB = 1024MB = 1024 * 1024 KB = 1024 * 1024 * 1024 Byte\)，所以可以得出一共需要\(4 \times 4 \times 2^{30} = 16GB\)

但是16GB在现在民用计算机中已经算比较大的内存占用了，而且一般操作系统也无法一次性开出这么大的连续空间，所以思路2在实际中也不可行

考虑一种新的思路：题目给出的是「一个数是否在这40亿个数中」，而「在和不在」只有两种情况：在以及不在，而刚好二进制0和1也可以表示两种状态，此时就可以考虑使用每一个比特位来标记某一个数值是否存在：如果存在则标记为1，不存在则标记为0

在新的思路中，使用比特位来标记数据是否存在的数据结构就称为「位图」

位图实现基本思路¶

位图本质是一个直接定址法的哈希表，每个整型值映射一个比特位，位图提供控制这个比特位的相关接口（主要关注「设置标记位set方法」、「恢复标记位reset方法」和「判断是否存在test方法」）

位图如何实现标记¶

在一个整型数字中，假设开辟一个长度为4的数组，则该数组中就有\(4 \times 32\)个比特位，如果此时存入一个数据就需要在对应位设置标记，但是在标记之前就需要知道这个数值是如何在位图中映射的

假设现在有一个数值23准备映射到位图中，因为是直接定址法，所以在长度为4的数组中映射位置下标为23

映射的思想已经成型，现在要考虑的就是如何找到映射位置，因为每一个整型数值有32个比特位，所以考虑下面的方案：

Note

引例：思路引入：一个人在第5组第8个位置，假设每一组有10个人，则该人在的位置就是\((5-1)\times10+8\) 问题：现在认为只知道每一组有10个人，知道一个人的位置在整个组中的第48个，问这个人在哪一组哪一个位置解决：首先求出这个人所在的组，用这个人的位置除以10：\(48 / 10 = 4\)，而因为\(40 < 48\)，所以这个人在第5组，而因为\(48 \mod 40 = 1......8\)，所以这个人在第8个位置，结合组和具体位置可以得出这个人在第5组第8个位置

假设插入的数值为\(x\)，则根据上面的引例可以有下面的步骤（一个整型数值占32个比特位）：

首先确定待映射的数值在第几个整数（类比引例中的「第几组」）：\(x / 32\)
接着确定待映射的数值在第几个比特位（类比引例中的「第几个位置」）：\(x \mod 32\)

通过上面的两个步骤就可以完全确定该数值的具体映射位置，例如数值23的映射位置为：第\(23 / 32 = 0\)个整数第\(23 \mod 32 = 23\)个比特位（下标）

Note

上面的下标是从1开始计算，直接将具体位置作为下标值

有了映射位置，就证明该数值已经有了对应的标记位置，接下来要处理的就是如何标记

所谓的标记，实际上就是将数值对应的映射位置置为1，最大的前提就是不能修改其他位置的标记，可以考虑下面的思路：

假设已经标记的整数二进制为00000100 01110000 00011000 00000000（左低右高），现在要标记第23个比特位，为了保证不改变其他比特位，可以考虑使用保留原值情况最多的或运算，假设将原二进制与1进行与运算，就可以得到下面的结果：

现在需要在第23个比特位处将0置为1，就需要在获取一个在第23个比特位为1其余比特位为0的整型数值，如果直接考虑这种数值，则根据计算器可以得到该数值：

可以看到这个数值非常大，而且如果依次列举，则时间复杂度也会特别高，所以可以考虑使用移位运算符，将10000000 00000000 00000000 00000000中的1移动到第23个比特位

Note

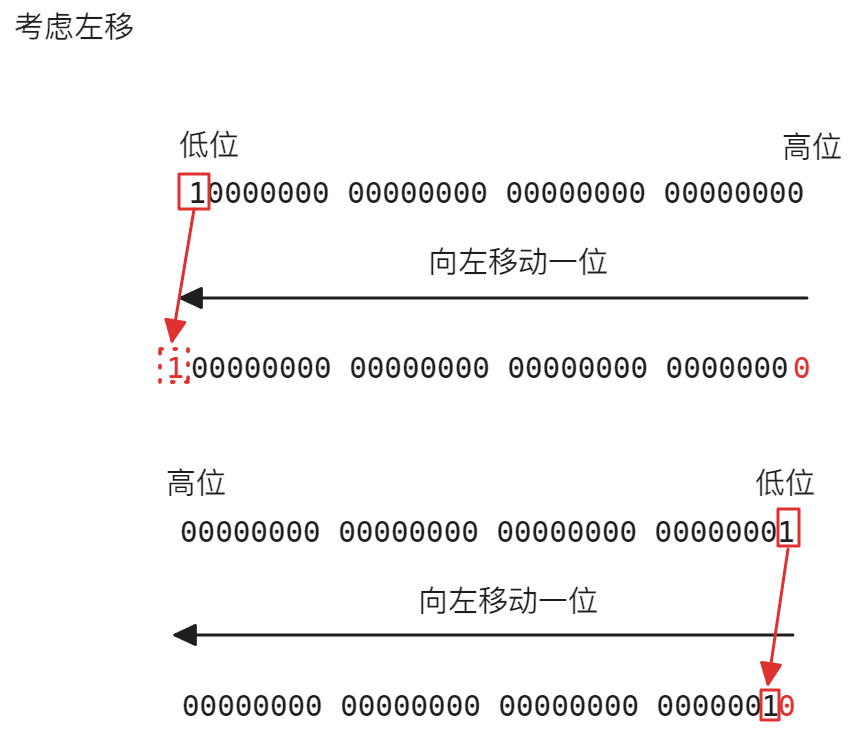
这一步可能会考虑到一个问题：大小端字节序在模拟移位过程中需要使用左移，在C语言/C++数组中，存储一个数值是从数组的低位开始存储，而一个数值存储到内存中在小端机器是按照小端字节序存储，大端机器按照大端字节序存储（具体内容见C语言部分讲解大端与小端字节序），此时就会出现既需要考虑数组的最低位以及数值的最低位，以考虑数值的最低位为例，可能会考虑到的效果：

但是实际上，可以不用考虑上面到底哪一侧是低位哪一侧是高位，因为在标准底层实现左移和右移时已经考虑到对应的机器的字节序了，所以左移真正的定义是「从低位向高位移动」，而不是「向左边移动」，右移则是「从高位向低位移动」，而不是「向右边移动」，所以正确的思路图如下，以左移为例：

所以结合或运算和与运算符就可以实现在映射位置标记（假设插入的数值为\(x\)）：

将最低位1通过左移运算符移动到第\(x\)个比特位
通过或运算符将移动1的数值与原二进制对应的数值进行或运算
将或运算结果赋值给对应的数值在数组中的下标位置「第几组」

位图如何取消标记¶

解决了如何实现标记，接下来考虑如何取消标记，以10000100 01110000 00011000 00000000为例，假设要取消从左往右数的第11个1，就要将第11个比特位的1置为0，而此时如果再使用或运算与1进行计算就无法达到需要的效果，剩下三种位运算：&、^和~

与运算和取反运算结合¶

考虑与运算的特点：同1为1，有0则0，如果进行与运算则结果如下：

可以发现，直接使用与运算符将原数值二进制和1相与会导致除了均为1的位以外其他全变成了0，违背了「不改变其他位的原则」，既然如此那么就反着来：「把1中比特位为1的变为0，把比特位为0的变成1」，所以考虑在与运算之前对1先进行取反运算，可以看到下面的效果：

可以看到原来全为1时的结果由1变成了0，其他位没有改变，所以本思路可行

异或运算¶

在使用「与运算和取反运算结合」结合时可以发现一个特点，需要的结果是「相同的为0（取消标记），不同为1（不改变标记）」，这个结果与异或运算的特点：异1同0，完全一致，以同样的二进制数值与1进行异或运算，下面是运算过程：

可以看到原来全为1时的结果由1变成了0，其他位没有改变，所以本思路也可行

结合左移运算符取消标记¶

前面使用了左移运算符，考虑此处是否可以使用左移运算符

首先需要获取到映射位置，方法与设置标记处相同：

假设插入的数值为\(x\)，则根据上面的引例可以有下面的步骤（一个整型数值占32个比特位）：

首先确定待映射的数值在第几个整数（类比引例中的「第几组」）：\(x / 32\)
接着确定待映射的数值在第几个比特位（类比引例中的「第几个位置」）：\(x \mod 32\)

以10000100 01110000 00011000 00000000为例（左低右高），取消第11个比特位的标记，可以考虑将1的二进制中为1的位左移11位，与运算和取反运算结合，计算结果如下：

可以看到需要取消标记的位已经置为了0，其他位也并没有影响，满足取消标记的要求

考虑异或运算是否也可以取消：

通过计算发现也可以做到同样的效果，满足取消标记的要求

所以结合「与运算符和取反运算符」和「左移运算符」就可以取消在映射位置标记（假设插入的数值为\(x\)）：

将最低位1通过左移运算符移动到第\(x\)个比特位
对移动后的1的二进制进行取反运算
将取反运算结果和原二进制对应的数值进行与运算
将与运算结果赋值给对应的数值在数组中的下标位置「第几组」

或者「异或运算符」和「左移运算符」（假设插入的数值为\(x\)）：

将最低位1通过左移运算符移动到第\(x\)个比特位
将移动后的1的二进制结果和原二进制对应的数值进行异或运算
将异或运算结果赋值给对应的数值在数组中的下标位置「第几组」

判断是否存在¶

所谓判断是否存在，就是判断指定数值是否在位图中，前面提到如果存在则对应二进制位为1，否则为0，所以只需要确定指定数值的映射位置是否为1即可判断指定数值是否存在

Note

此处注意一个细节：任何一个数值只要不是0，其二进制位至少存在一位为1

位图代码实现¶

C++
namespace simulate_bitset
{
    template <size_t N>
    class bitset {
    public:
        bitset()
        {
            // 提前开辟空间，为了保证空间在65/32这种情况下依旧有空间，可以多开辟一个无符号整型的空间
            _bs.resize(N / (sizeof(int) * 8) + 1);
        }

        // 设置标记
        void set(size_t num)
        {
            // 找到映射位置
            size_t pos_group = num / (sizeof(int) * 8);
            size_t pos_detail = num % (sizeof(int) * 8);

            // 左移+或运算
            _bs[pos_group] |= (1 << pos_detail);
        }

        // 取消标记
        void reset(size_t num)
        {
            // 找到映射位置
            size_t pos_group = num / (sizeof(int) * 8);
            size_t pos_detail = num % (sizeof(int) * 8);

            // 左移+取反运算+与运算
            // _bs[pos_group] &= (~(1 << pos_detail));
            // 左移+异或运算
            _bs[pos_group] ^= (1 << pos_detail);
        }

        // 测试
        bool test(size_t num)
        {
            // 找到映射位置
            size_t pos_group = num / (sizeof(int) * 8);
            size_t pos_detail = num % (sizeof(int) * 8);

            // 判断指定位是否为1
            return _bs[pos_group] & (1 << pos_detail);
        }

    private:
        std::vector<int> _bs;
    };
}

Note

注意，上面位图不考虑负数的情况，否则会导致未定义行为，如果将三个函数的参数类型已经位置变量类型改为int，在g++可能可以成功，但是这个结果不是确定的

位图的优缺点¶

优点：增删查改快，节省空间

缺点：只适用于整形

位图相关考察题目¶

给定100亿个整数，设计算法找到只出现一次的整数
给两个文件，分别有100亿个整数，只有1G内存，如何找到两个文件交集
一个文件有100亿个整数，只有1G内存，设计算法找到出现次数不超过2次的所有整数

第一个问题和第三个问题基本是一致的，考虑第一个问题，「只出现一次」则可以分为三种情况：

没出现
出现一次
出现两次及以上

此时只使用前面的一位作为标记位就不够了，需要使用两个标记位，所以上面的三种情况对应的二进制位分别为：

没出现：00
出现一次：01
出现两次：10

以100个无符号整数为例，所以对应的bitset结构可以为如下代码：

C++
template <size_t N>
class bitsetForTwo {
public:
    void set(size_t num)
    {
        if(!_bs1.test(num) && !_bs2.test(num))
        {
            // 一次没出现
            _bs2.set(num); // 00 -> 01
        }
        else if (!_bs1.test(num) && _bs2.test(num))
        {
            // 出现一次 01 -> 10
            _bs1.set(num);
            _bs2.reset(num);
        }
    }

    bool test(size_t num)
    {
        return !_bs1.test(num) && _bs2.test(num);
    }

private:
    simulate_bitset::bitset<100> _bs1;
    simulate_bitset::bitset<100> _bs2;
};

第三个问题只需要获取不超过两次的数值（以100个无符号整数为例）即可，基本思路与第一个问题一致，修改代码如下：

C++
template <size_t N>
class bitsetForTwo {
public:
    void set(size_t num)
    {
        if(!_bs1.test(num) && !_bs2.test(num))
        {
            // 一次没出现
            _bs2.set(num); // 00 -> 01
        }
        else if (!_bs1.test(num) && _bs2.test(num))
        {
            // 出现一次 01 -> 10
            _bs1.set(num);
            _bs2.reset(num);
        }
        else if (_bs1.test(num) && !_bs2.test(num))
        {
            // 出现两次 10 -> 11
            _bs1.set(num);
            _bs2.set(num);
        }
    }

    bool test(size_t num)
    {
        return (!_bs1.test(num)) && _bs2.test(num) || _bs1.test(num) && (!_bs2.test(num)) || _bs1.test(num) && !_bs2.test(num);
    }

private:
    simulate_bitset::bitset<100> _bs1;
    simulate_bitset::bitset<100> _bs2;
};

考虑第二个问题（以100个无符号整数为例），所谓交集，就是两个位图同时为1，即取出11，测试代码如下：

C++
int main()
{
    simulate_bitset::bitset<100> _bs2;
    simulate_bitset::bitset<100> _bs3;

    int a1[] = { 5,7,9,2,5,99,5,5,7,5,3,9,2,55,1,5,6 };
    int a2[] = { 5,3,5,99,6,99,33,66};
    // 插入数据
    for (auto a : a1)
    {
        _bs2.set(a);
    }

    for (auto a : a2)
    {
        _bs3.set(a);
    }

    for(size_t i = 0; i < 100; i++)
    {
        if(_bs2.test(i) && _bs3.test(i))
        {
            std::cout << i << std::endl;
        }
    }
    return 0;
}