栈¶

约 834 个字 111 行代码 1 张图片预计阅读时间 4 分钟

栈介绍¶

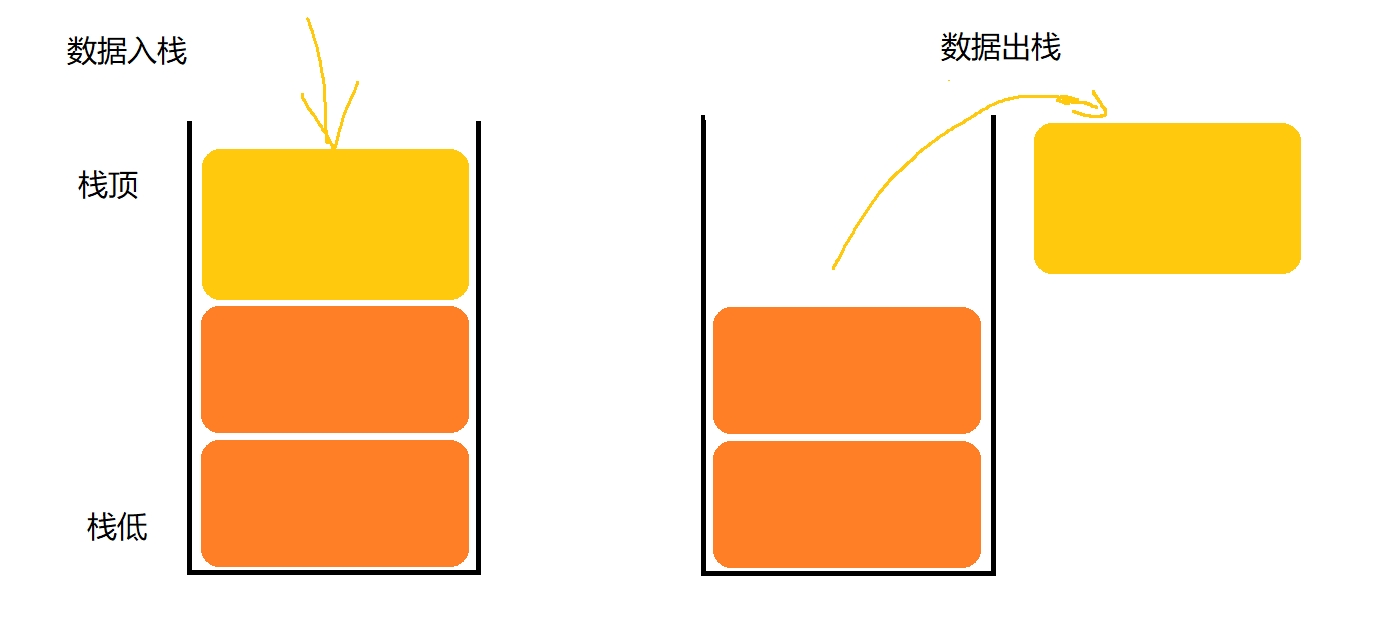
栈是一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。

压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。

出栈：栈的删除操作叫做出栈。出数据也在栈顶。

Note

注意在栈中数据出栈的顺序不一定和入栈的顺序相同，当数据入栈后又出栈不影响下一个数据的入栈顺序

例如：

入栈1 2 3 4 5，若4和5是入栈又出栈的，则出栈的顺序应该是4 5 3 2 1

但是不会出现一种情况，即：

已经入栈的数据（未在入栈后立马出栈）不会出现在先入栈又立马出栈的数据的前方

例如：

入栈 1 2 3 4，若3和4是入栈又立马出栈，则不可能出现2和1在3和4的前面若进栈序列为 1,2,3,4 ，进栈过程中可以出栈，则下列不可能的一个出栈序列是（C）

A 1, 4, 3, 2

B 2, 3, 4, 1

C 3, 1, 4, 2

D 3, 4, 2, 1

例如本题中，入栈顺序为1, 2, 3, 4，那么出栈顺序最基本的就是先入先出，即出栈顺序为4,3,2,1，如果入栈又立马出栈的是2,3,4，则有2,3,4,1，如果入栈又立马出栈的是1，则有1, 4, 3, 2，如果入栈又立马出栈的是3, 4，则有3, 4, 2, 1，但是不可能存在3, 1, 4, 2，因为1作为第一个入栈的，要么就是入栈又立马出栈，作为第一个出栈的，要么就是最后一个出栈的

栈的实现¶

栈的实现一般可以使用数组或者链表实现，相对而言数组的结构实现更优一些。因为栈满足先进先出或者即进即出，不需要额外移动数据，并且数组在尾上插入数据的代价比较小。

数组栈¶

C
//静态数组栈
typedef int STDataType;
#define N 10
typedef struct Stack
{
    STDataType _a[N];// 数组大小固定
    int _top; // 栈顶
}ST;

//动态数组栈
typedef int STDataType;
typedef struct Stack
{
    STDataType* _a;// 数组大小不固定
    int _top;       // 栈顶
    int _capacity;  // 容量 
}ST;

数组栈的实现¶

C
//主要实现以下功能

//栈的初始化
void STInit(ST* st);
//栈的销毁
void STDestroy(ST* st);
//数据入栈
void STPush(ST* st, STDataType x);
//数据出栈
void STPop(ST* st);
//判断栈是否为空
bool STEmpty(ST* st);
//获取栈元素
STDataType STTop(ST* st);
//获取栈数据个数
int STSize(ST* st);

栈的初始化¶

在初始化过程中注意top的初始值设置为0代表栈内数据的下一个位置，因为初始化栈代表栈内没有元素，如果用0代表栈内数据的当前位置，那么需要考虑该元素从何而来，既然没有数据，说明当前栈顶指针指向没有数据的位置，而数组下标为0代表第一个元素的位置，没有元素就不可能有第一个元素的位置，所以此时下标为0代表下一个元素的位置，此时说明栈内没有元素，但是准备在下一个位置（第一个元素）的位置添加数据

C
//栈的初始化
void STInit(ST* st)
{
    //判断是否存在队列
    assert(st);
    //初始化队列
    st->data = NULL;
    st->top = 0;//栈顶指针指向存储数据的下一个位置，代表栈内无数据
    //st->top = -1;//栈顶指针指向存储数据的位置，代表栈内无数据
    st->capacity = 0;
}

栈的销毁¶

C
//栈的销毁
void STDestroy(ST* st)
{
    //确保有栈的存在
    assert(st);
    //销毁栈
    free(st->data);
    st->data = NULL;
    //top和capacity更改为无数据的位置
    st->top = st->capacity = 0;
}

数据入栈¶

C
//数据入栈
void STPush(ST* st, STDataType x)
{
    //确保有栈的存在
    assert(st);
    //向top位置增加数据，并使top向后移动
    //需要判断栈的容量大小
    if (st->top == st->capacity)
    {
        //如果栈的空间为0，则开辟四个空间，如果栈容量不为0，则扩容原来容量的2倍
        int newCapacity = st->capacity == 0 ? 4 : st->capacity * 2;
        STDataType* tmp = (STDataType*)realloc(st->data, sizeof(STDataType) * newCapacity);
        assert(tmp);
        st->data = tmp;
        //注意更新容量大小
        st->capacity = newCapacity;
    }

    //数据压栈并改变top
    st->data[st->top++] = x;
}

判断栈是否为空¶

C
//判断栈是否为空
bool STEmpty(ST* st)
{
    //确保有栈的存在
    assert(st);
    //栈为空返回真，栈不为空返回假
    return st->top == 0;//判断表达式返回值只有1和0，如果为真返回1(true)，如果为假返回0(false)
}

数据出栈¶

C
//数据出栈
void STPop(ST* st)
{
    //确保有栈的存在
    assert(st);
    //确保栈不会越界
    assert(!STEmpty(st));

    //直接移动top指针，“看不见即删除”
    st->top--;
}

获取栈顶元素¶

C
//获取栈顶元素
STDataType STTop(ST* st)
{
    //确保栈存在
    assert(st);
    //确保栈不为空
    assert(!STEmpty(st));
    //top为栈内数据的下一个位置，要获取当前位置的元素需要-1操作
    return st->data[st->top - 1];
}

获取栈内数据个数¶

C
//获取栈内数据个数
int STSize(ST* st)
{
    assert(st);
    return st->top;
}

栈¶