跳转至

树的基本概念

约 724 个字 7 行代码 4 张图片 预计阅读时间 3 分钟

树的概念和结构

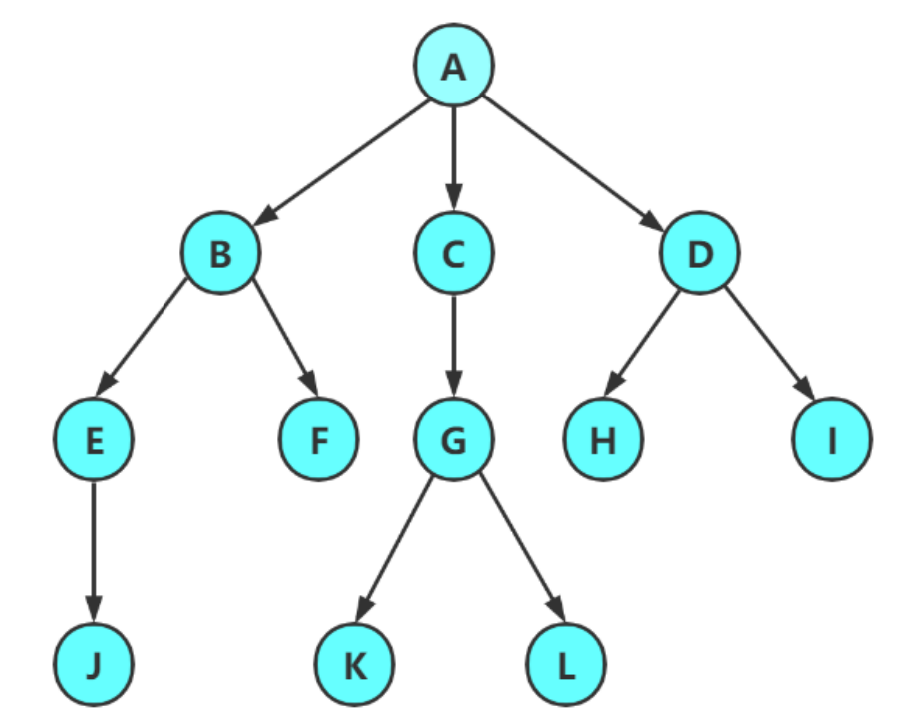
树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合

Note

把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的

树的相关概念

Note

树的概念是以现实中的树的结构以及人类的亲缘关系决定的

  1. 根节点：根节点为树的第一个节点，该节点没有前驱节点（即没有父亲节点）

  2. 节点的度：一个节点包含的直接子树（如果子树还有其它子树，则当做整体看待）的数量即为节点的度的大小

  3. 树的度：一个树的度为最大的节点的度

  4. 叶节点（或终端节点）：度为0的节点

  5. 分支节点（或非终端节点）：度不为0的节点（A即是根节点，也是分支节点）

  6. 父节点（或双亲节点）：若一个节点含有子节点，则该节点为其子节点的父节点

  7. 子节点（或孩子节点）：一个节点含有的子树的父节点称为该节点的子节点

  8. （亲）兄弟节点：具有相同的父节点的节点互称为兄弟节点

  9. 堂兄弟节点：子节点父节点在同一层的子节点互称为堂兄弟节点

  10. 节点的层次：从根节点开始，根为第一层，根的子节点为第二层，以此类推（节点的层次建议从1开始计算）

  11. 树的高度：树中任意一个节点到叶子节点的距离（叶子节点的位置高度为1，则最小高度为1，即叶子节点所在层）

  12. 树的深度：树中任意一个节点到根节点的距离（根节点的位置深度为1，则最小高度为1，即根节点所在层）

  13. 节点的祖先：从根到该所经过的分支上的所有节点

  14. 子孙：以某节点为根的子树中任一节点都称为该节点的子孙

  15. 森林：由m（m>0）棵互不相交的树的集合称为森林（应用：并查集）

树的特点

除根节点外，其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm，其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱，可以有0个或多个后继，因此，树是递归定义（根节点（A）→子节点（B）→父节点（B）→子节点（E）→父节点（E）→叶子节点（J））的

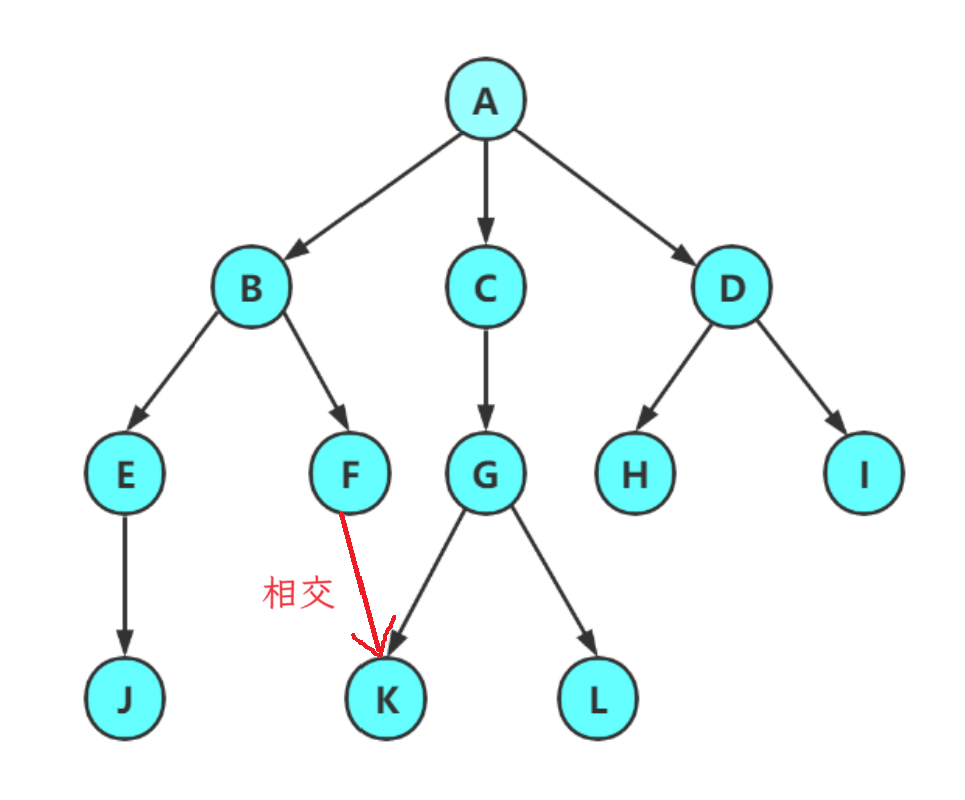
树形结构中，子树之间不能有交集，否则就不是树形结构

Note

树的相交：

即两个父节点共用一个子节点，如下图所示：

树的表示

树结构相对线性表就比较复杂了，要存储表示起来就比较麻烦了，既要保存值域，也要保存结点和结点之间的关系，实际中树有很多种表示方式如：双亲表示法，孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。这里就简单的了解其中最常用的孩子兄弟表示法

C
1
2
3
4
5
6
7
typedef int TNDataType;
struct TreeNode
{
    struct TreeNode* child; //存储孩子节点的地址
    struct TreeNode* brother; //存储兄弟节点的地址
    TNDataType data; //存储数据 
}

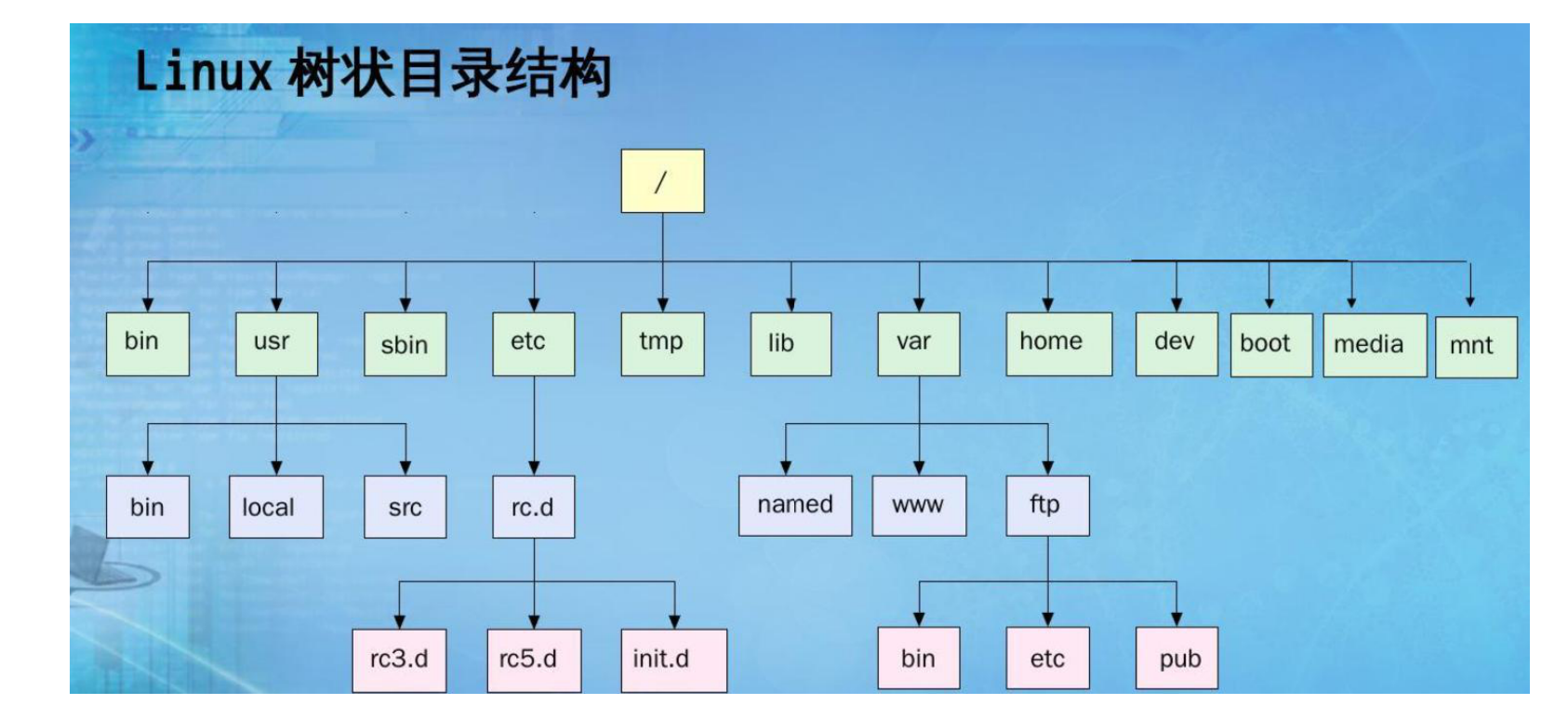
树的基本应用

文件系统的目录树