跳转至

堆

约 2396 个字 424 行代码 17 张图片 预计阅读时间 13 分钟

堆的介绍

如果有一个关键码的集合，把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中，则称为堆

将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆

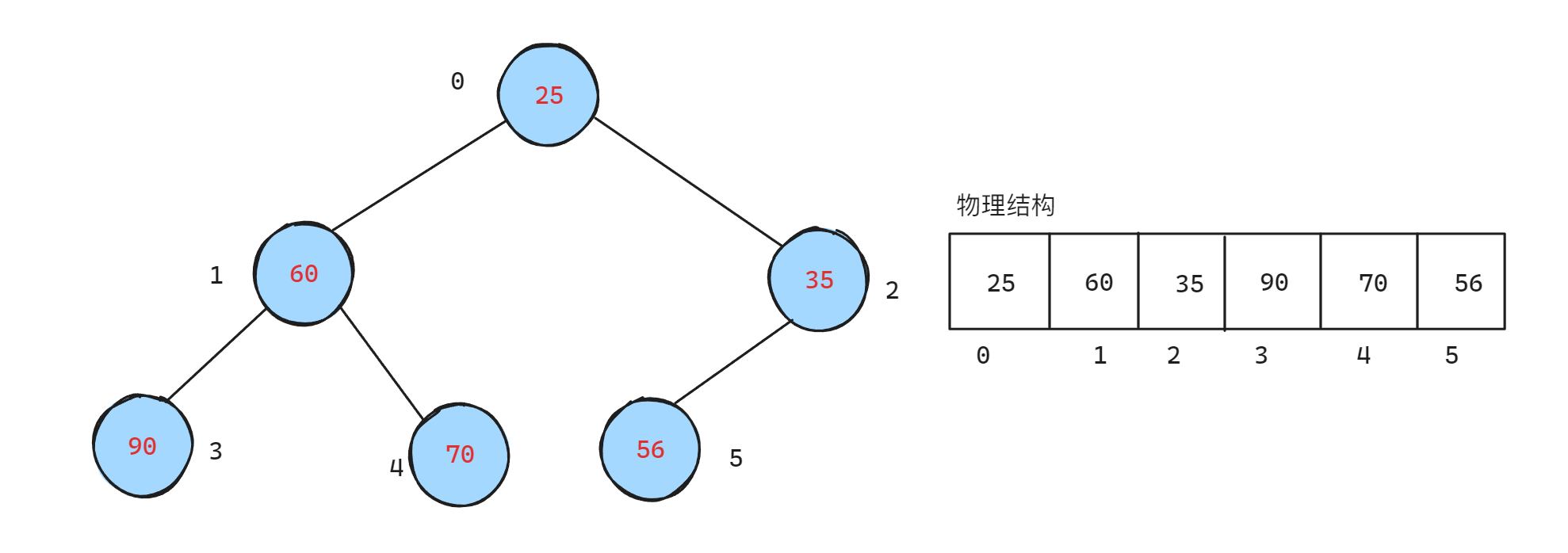
堆的特点：

  1. 堆总是一棵完全二叉树
  2. 堆中某个节点的值总是不大于或不小于其父节点的值

  3. 二叉树中父子间下标关系：

    • 孩子节点找父亲节点：

      1. 左孩子：leftChild = parent * 2 + 1（根节点下标为0，左孩子的下标总是奇数）
      2. 右孩子：rightChild = parent * 2 + 2（即leftChild + 1。根节点下标为0，右孩子的下标总是偶数）

    • 父亲节点找孩子节点：parent = (child - 1) / 2。这个公式不论孩子节点下标为奇数还是偶数均可以使用，因为当child为奇数时，会进行取整操作

堆的实现

堆的类型定义

C
1
2
3
4
5
6
7
8
9
// 定义堆中存储的数据的数据类型
typedef int HPDataType；
// 堆的结构设计
typedef struct Heap
{
    HPDataType* data;// 存储数据部分
    int size; // 堆中的有效数据个数
    int capacity; // 堆的容量大小
}HP;

堆的功能实现（以小堆为例）

C
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
// 主要实现功能
// 堆的初始化
void HeapInit(HP* hp);
// 堆的销毁
void HeapDestroy(HP* hp);
// 堆的数据插入
void HeapPush(HP* hp, HPDataType x);
// 堆的数据删除
void HeapPop(HP* hp);
// 获取堆顶数据
HPDataType HeapTop(HP* hp);
// 判断堆是否为空
bool IsEmpty(HP* hp);

堆的初始化

C
1
2
3
4
5
6
// 堆的初始化
void HeapInit(HP* hp)
{
    hp->data = NULL;
    hp->size = hp->capacity = 0;   
}

堆的销毁

C
1
2
3
4
5
6
7
// 堆的销毁
void HeapDestroy(HP* hp)
{
    assert(hp);
    free(hp->data);
    hp->size = hp->capacity = 0;
}

堆的数据插入

对于堆的数据插入过程来说（以小堆为例），在小堆中，父亲节点的值总小于或等于孩子节点的值，故可以采用向上调整算法，但是使用向上调整算法的前提是除插入数据以外，原始的堆已经为小堆

C
1
2
//以下面的数组为例
int arr[6] = { 35,70,56,90,60,25};

Note

注意，判断循环条件为child > 0，而不是parent >= 0，因为当child为0时，说明已经到了根节点，就不需要再进行向上调整了，而如果使用parent >= 0作为循环条件，那么当child为0时，parent = (child - 1) / 2算出来的值依旧是0，从而多进行一次无意义的比较再break

C
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
//交换函数
void swap(HPDataType* num1, HPDataType* num2)
{
    HPDataType* tmp = num1;
    *num1 = *num2;
    *num2 = *tmp;
}

//向上调整算法
void AdjustUP(HPDataType* data, int size, int child)
{
    int parent = (child - 1) / 2;//计算父亲节点的位置
    while (child > 0)
    {
        if (data[child] < data[parent])
        {
            //交换孩子节点和父亲节点的值
            swap(&data[child], &data[parent]);

            child = parent;//更新孩子节点为原父亲节点的位置
            parent = (child - 1) / 2;// 获取下一个父亲节点的位置
        }
        else
        {
            break;// 如果有一次出现孩子节点大于父亲节点的值就直接跳出不需要进行接下来的比较，因为其他位置在执行前已经是小堆
        }
    }
}

// 堆的数据插入
void HeapPush(HP* hp, HPDataType x)
{
    assert(hp);
    //判断是否需要扩容
    if (hp->size == hp->capacity)
    {
        int newCapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;
        HPDataType* tmp = (HPDataType*)realloc(sizeof(HPDataType) * newCapacity);
        assert(tmp);
        hp->data = tmp;
        hp->capacity = newCapacity;
    }
    hp->data[hp->size++] = x;
    //插入数据
    //以小堆为例，在小堆中，父亲节点的值总小于或等于孩子节点的值
    //所以需要进行向上调整
    //向上调整的前提是其余的内容已经是小堆
    AdjustUP(hp->data, hp->size, hp->size - 1);
}

堆的数据移除

在堆中，移除的数据均为堆的第一个数据，即根节点的数据，但是不能直接使用挪动覆盖的思路，因为会打破原有的堆结构，可以采用先交换根节点和叶子节点的数据再使用向下调整算法恢复小堆结构

先交换根节点和叶子节点的数据，再改变size的值，从而达到删除数据的效果

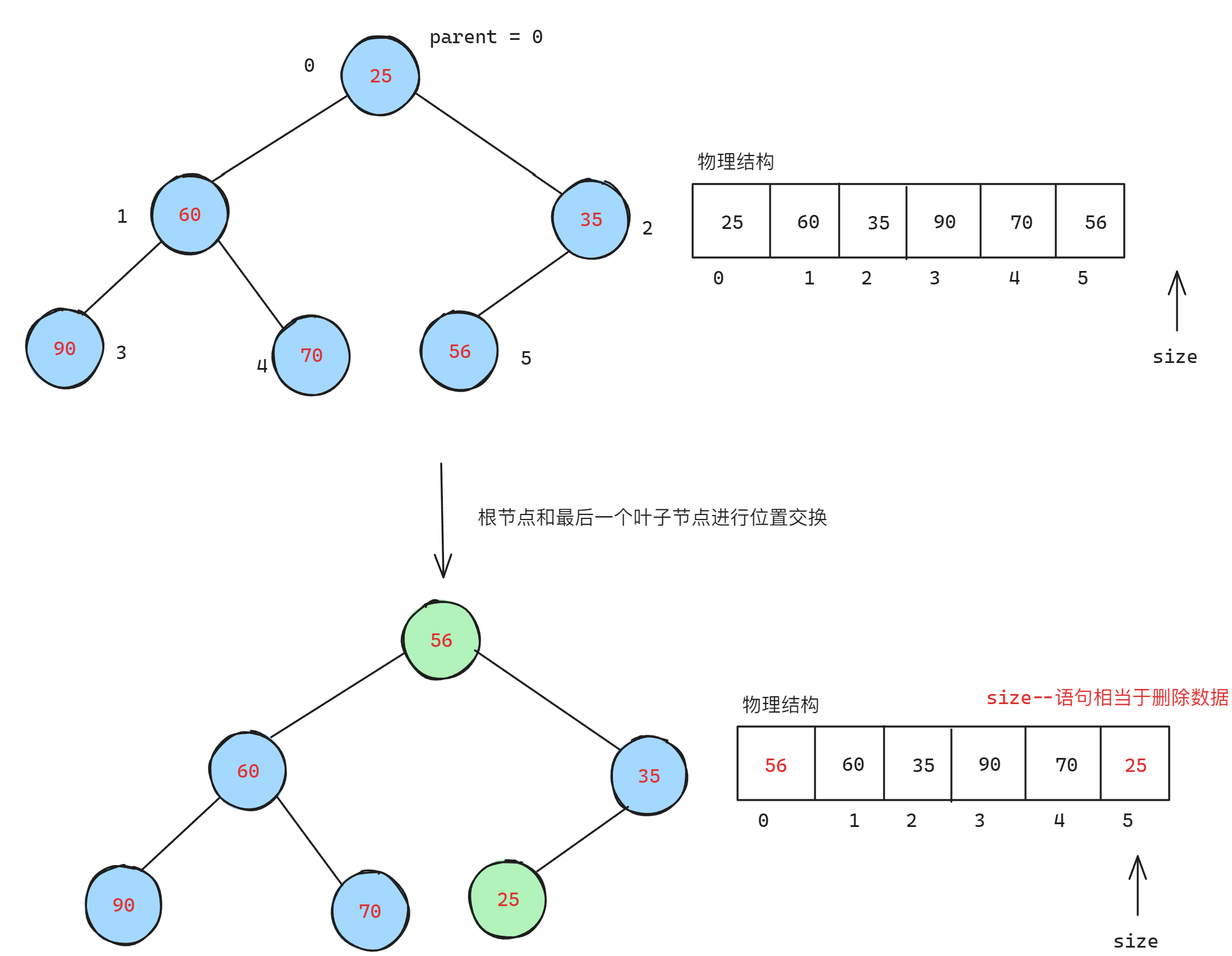
接着执行向下调整算法恢复堆结构

在执行向下调整算法时，需要判断是和哪一个孩子节点进行交换，找到较小的孩子的节点交换即可

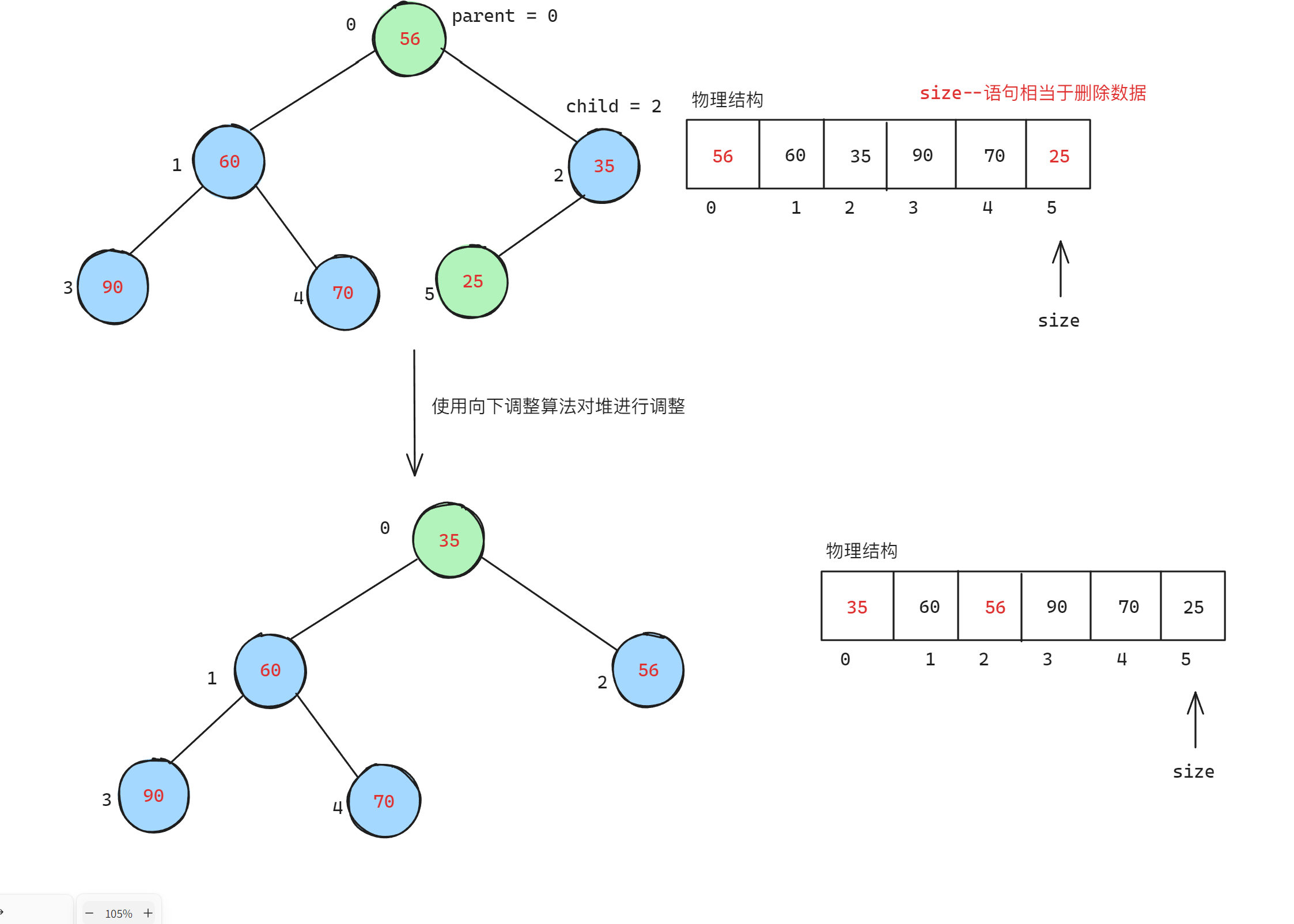
C
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
//向下调整算法
void AdjustDown(HPDataType* data, int size, int parent)
{
    int child = parent * 2 + 1;//假设左边的孩子节点为较小的孩子节点
    while (child < size)
    {
        //如果假设不正确，则改变需要进行交换的孩子节点
        if (child + 1 < size && data[child] > data[child + 1])//先判断child+1是否越界
        {
            child++;// 将child更改为右边的孩子节点
        }
        //执行交换
        if (data[child] < data[parent])
        {
            swap(&data[child], &data[parent]);

            parent = child;//更新parent值便于继续比较下一层
            child = parent * 2 + 1;//更新child的值
        }
        else
        {
            break;
        }
    }
}

// 堆的数据删除
void HeapPop(HP* hp)
{
    assert(hp);
    //堆为空不执行删除操作
    assert(!IsEmpty(hp));

    //在堆中，删除的数据并不是最后一个元素，而是第一个元素
    //但是不可以直接挪动数据，否则会改变节点之间的关系，从而失去堆的结构
    //可以考虑使用先交换根节点和最后一个叶子节点数据再使用向下调整算法解决问题
    //交换根节点数据和最后一个叶子节点数据
    swap(&(hp->data[0]), &(hp->data[hp->size - 1]));
    hp->size--;
    //向下调整算法恢复堆结构
    AdjustDown(hp->data, hp->size, 0);
}

判断堆是否为空

C
1
2
3
4
5
6
// 判断堆是否为空
bool IsEmpty(HP* hp)
{
    assert(hp);
    return hp->size == 0;
}

获取堆顶数据

C
1
2
3
4
5
6
7
8
//获取堆顶数据
HPDataType HeapTop(HP* hp)
{
    assert(hp);
    assert(!IsEmpty(hp));

    return hp->data[0];
}

获取堆的有效数据个数

C
1
2
3
4
5
6
//获取堆的有效数据个数
int HeapSize(HP* hp)
{
    assert(hp);
    return hp->size;
}

堆排序算法

堆排序原理分析（小堆为例）

所谓堆排序，就是通过堆的插入和删除的特点实现对数组内的数据进行排序

在堆的插入过程中，存在向上调整算法，对于小堆来说，每一次向上调整都会进行数值的大小比较，而较小的数值会被移动到父亲节点的位置，较大的数值会被移动到孩子节点的位置，如下图所示

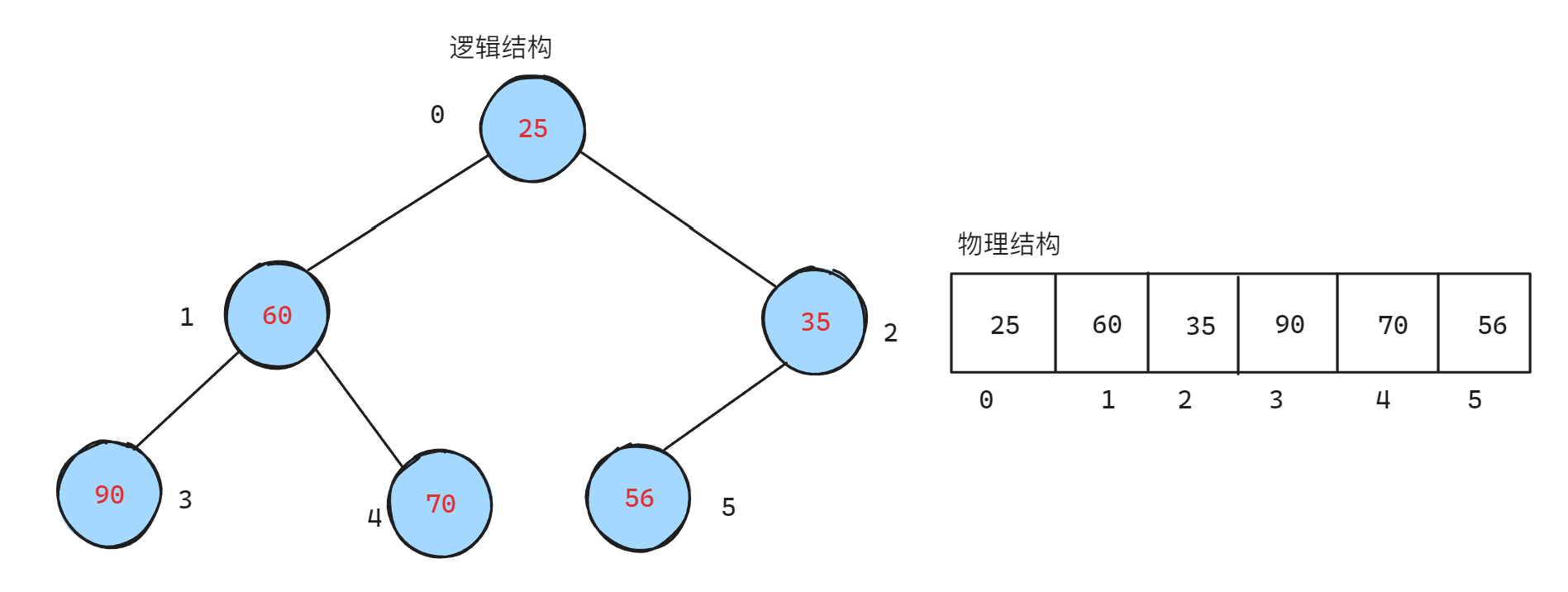
而在堆的删除过程中，存在向下调整算法，对于小堆来说，每一次的删除之前，都需要将根节点的数值和最后一个叶子节点的数值进行位置交换，因为根节点的数据最小，所以每一次的位置交换都会将当前剩余部分的最小值放在最末尾，如果先打印根节点的数值，再执行删除，那么就会实现数据的升序排序，如下图所示

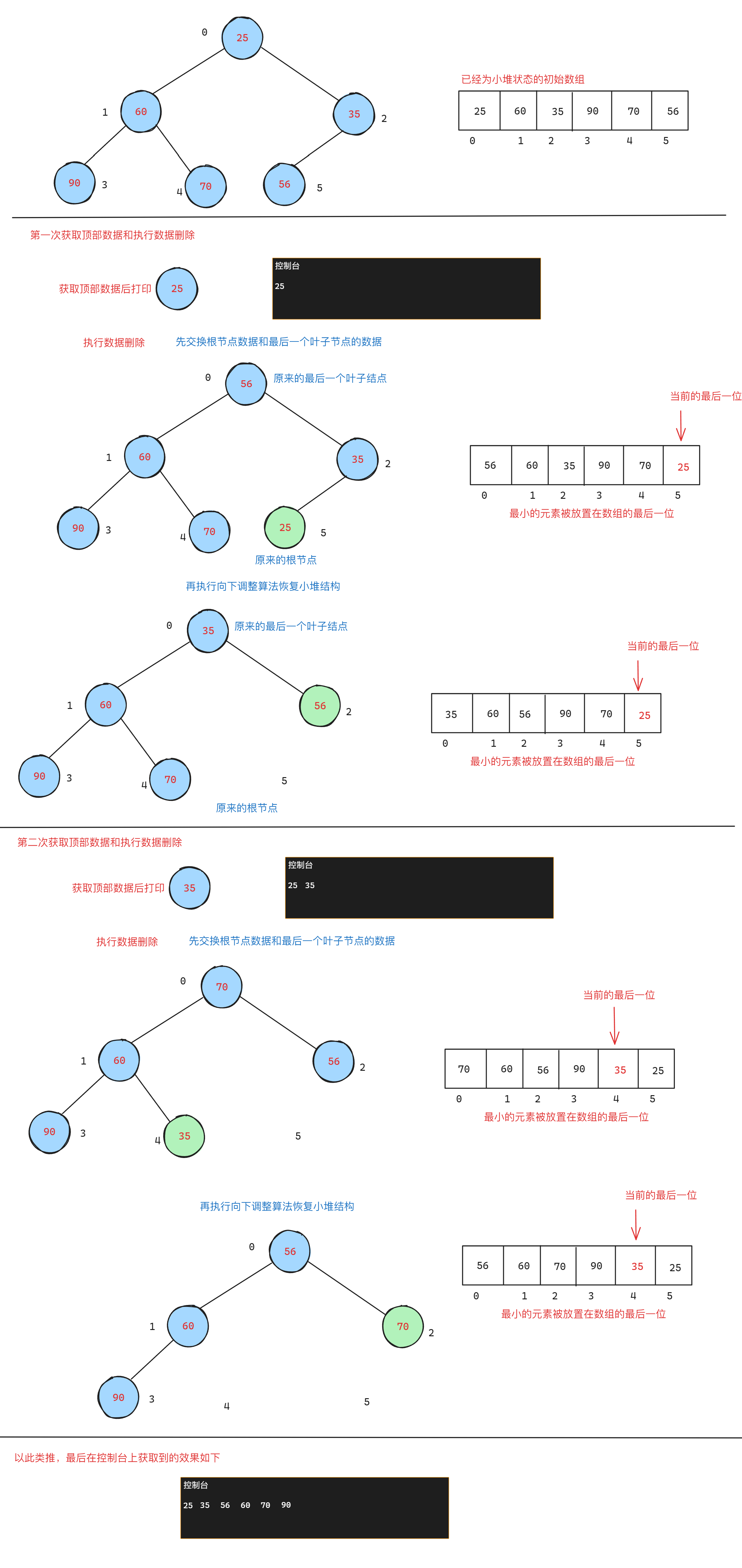
向上调整建堆+向下调整排序（小堆为例）

上面的思路是建立在已经实现了堆的数据结构以及相应功能，如果不存在该结构，则无法直接使用该排序，过程相对繁琐，所以可以考虑单独抽出向上调整算法和向下调整算法直接进行排序算法的实现，因为从排序开始到排序结束，只会用到向上调整算法实现数组数据到堆的构建，以及向下调整算法对数据进行重新整理，而控制台能看到升序的数值是因为在每次删除数据之前都进行了一次根节点数据的取出，在小堆中，根节点数据为最小的数值，所以最后实现一个升序的效果

但是，如果在不实现堆的相关功能的情况下实现堆排序算法，则需要考虑到如何使任意数组形成堆以及如何进行排序

首先，如何使任意数组形成堆结构

对于该问题，可以直接使用向上调整算法在原数组的基础上对其数据进行修改从而形成堆的结构，以小堆为例

C
1
2
//以下面的数组为例
int data[] = { 7,8,3,5,1,9,5,4 };

注意在设计向上调整算法的函数时，传入的控制数组大小的参数为下标i而不是数组的整体大小，如果用数组的整体大小，则需要从最后一个元素进行向上比较，但是需要注意的问题是，在左右孩子节点均存在时，需要比较左右孩子节点的大小，再与父亲节点比较判断是否需要进行交换

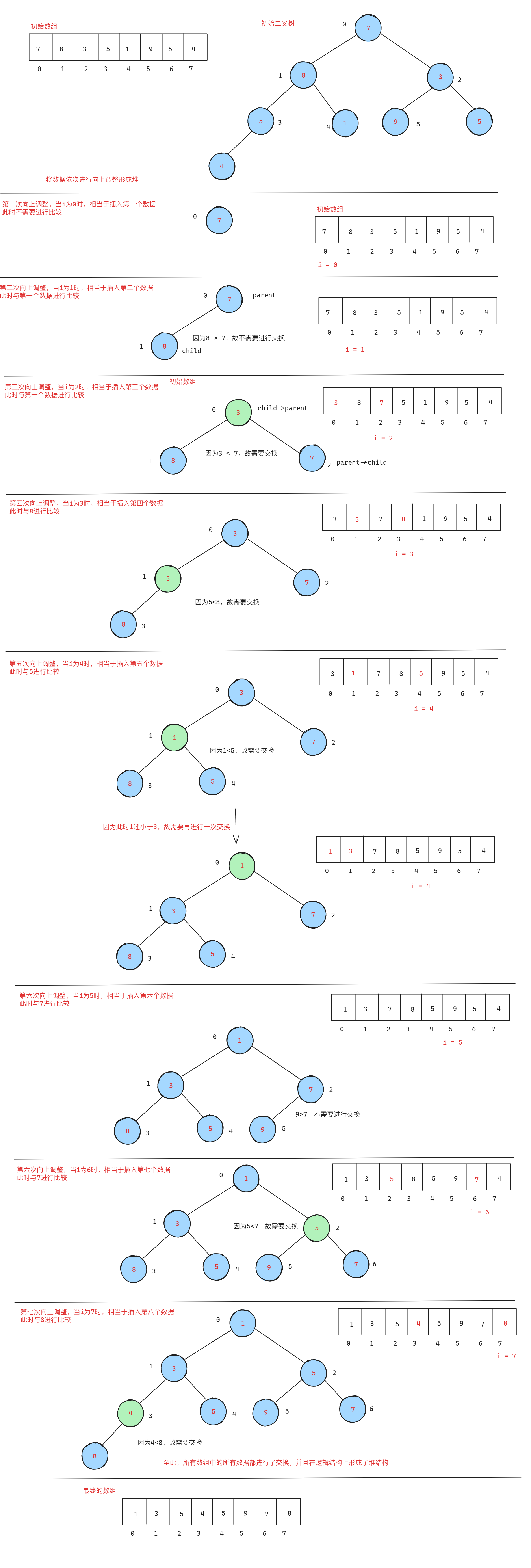
接下来处理第二个问题，如何进行排序

在前面有堆的数据结构及实现的基础上，了解到当使用小堆时，会将数组排成升序，但是在没有先打印堆顶数据的情况下，会将数组排成降序。因为升序的本质就是先打印末尾元素，再依次打印前面的元素从而实现升序，所以如果不打印，默认最小的元素就在末尾，前面的元素都比其后一个元素大，所以就是降序。过程如下：

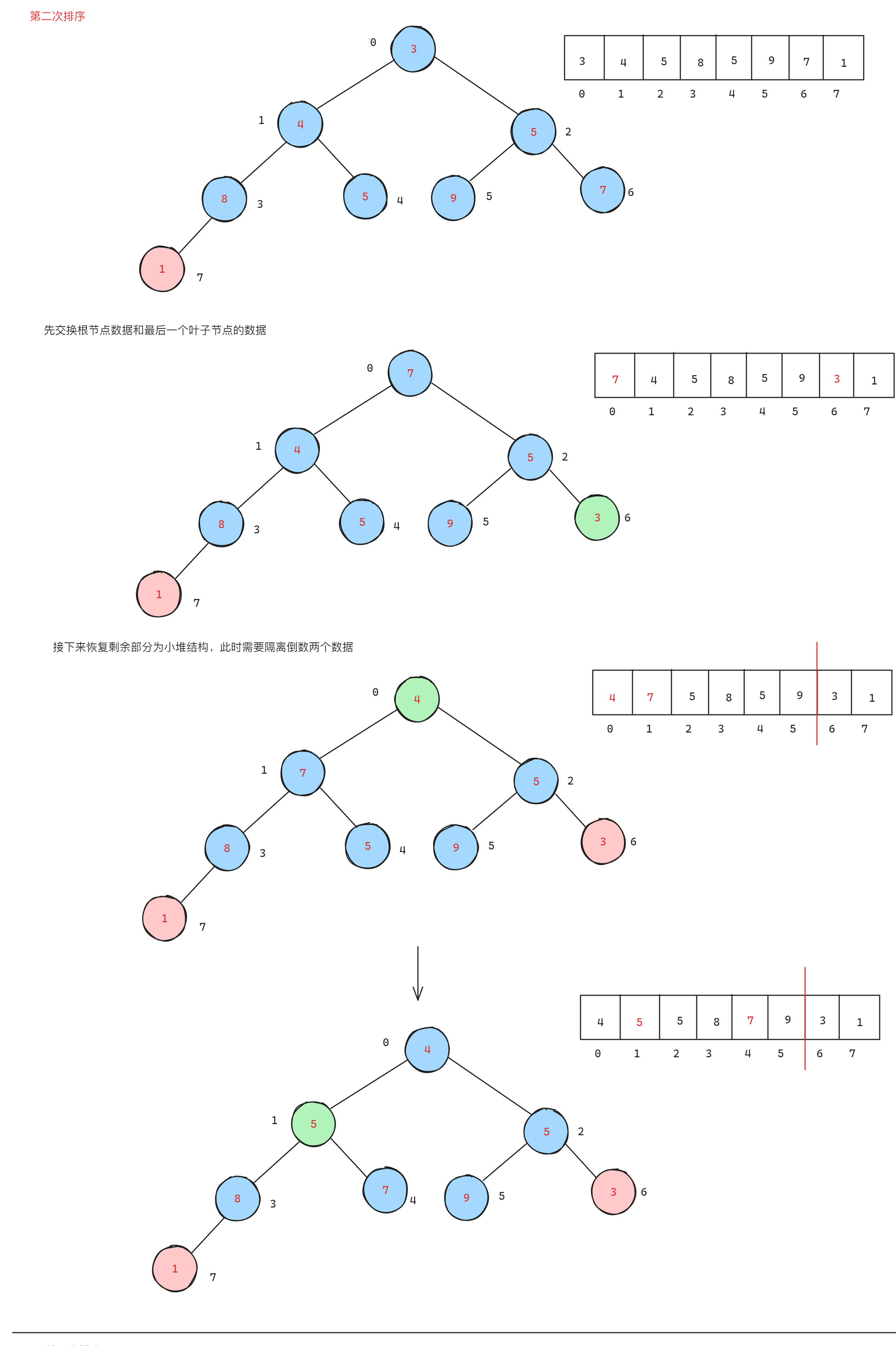
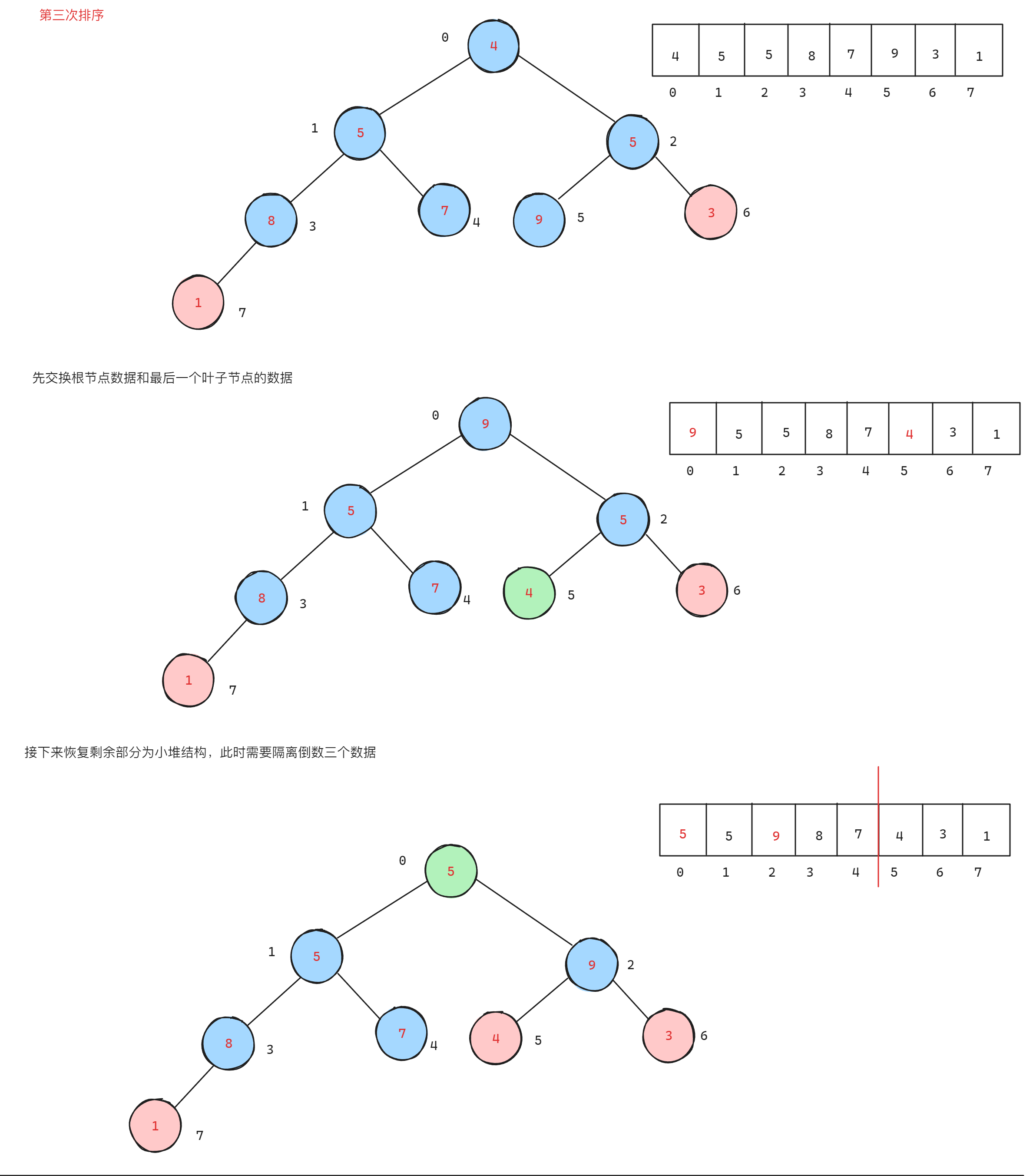
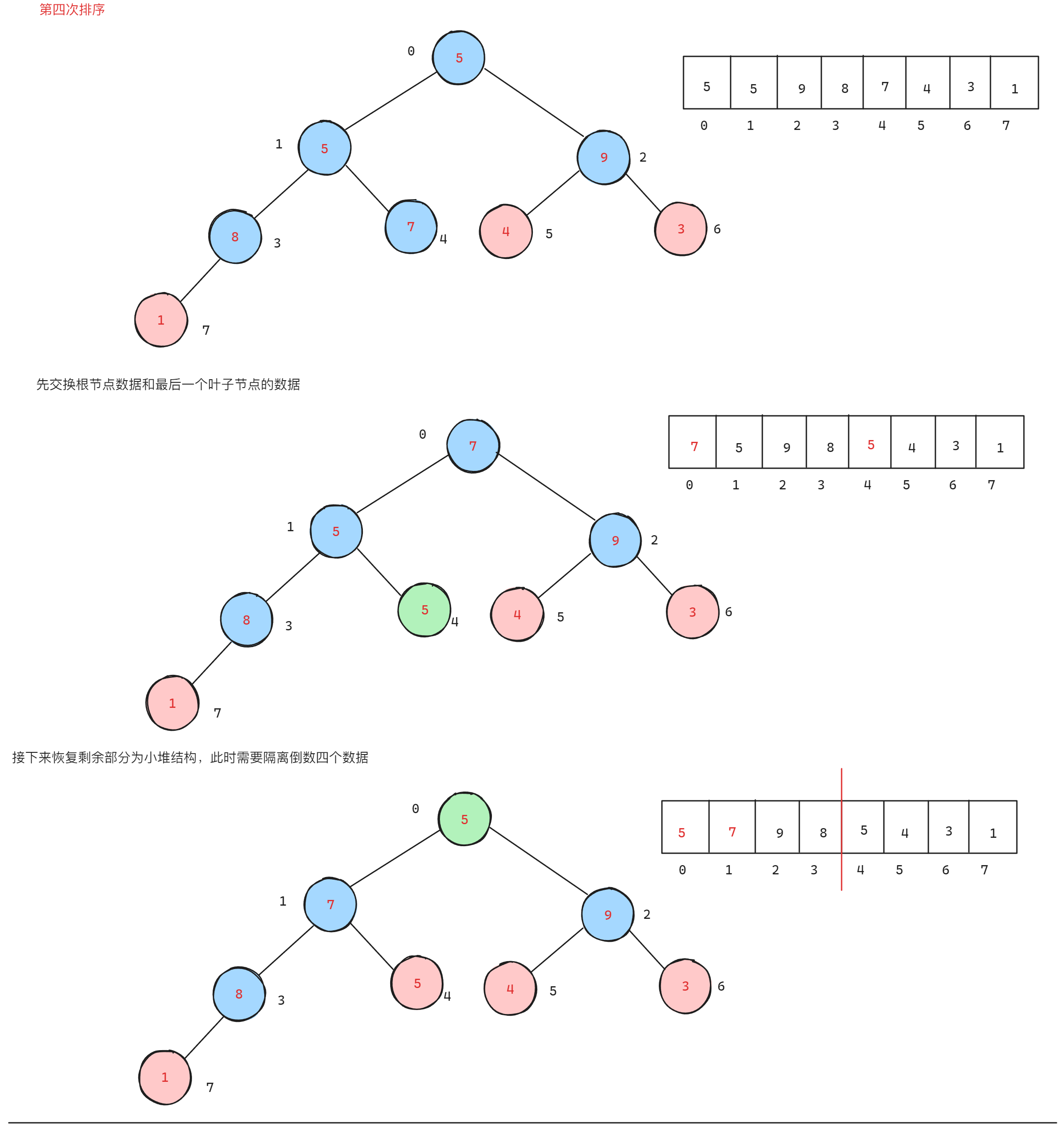
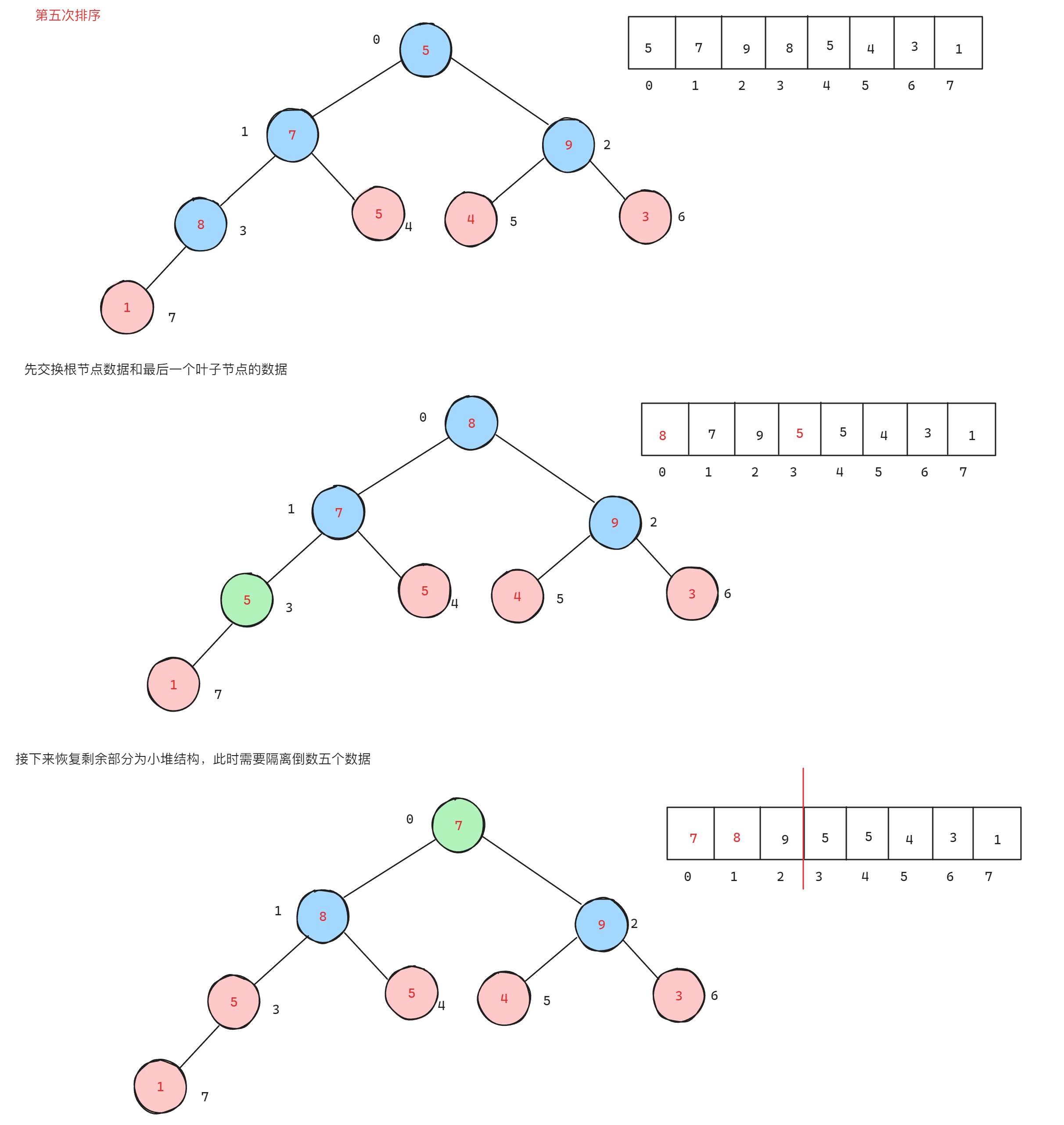
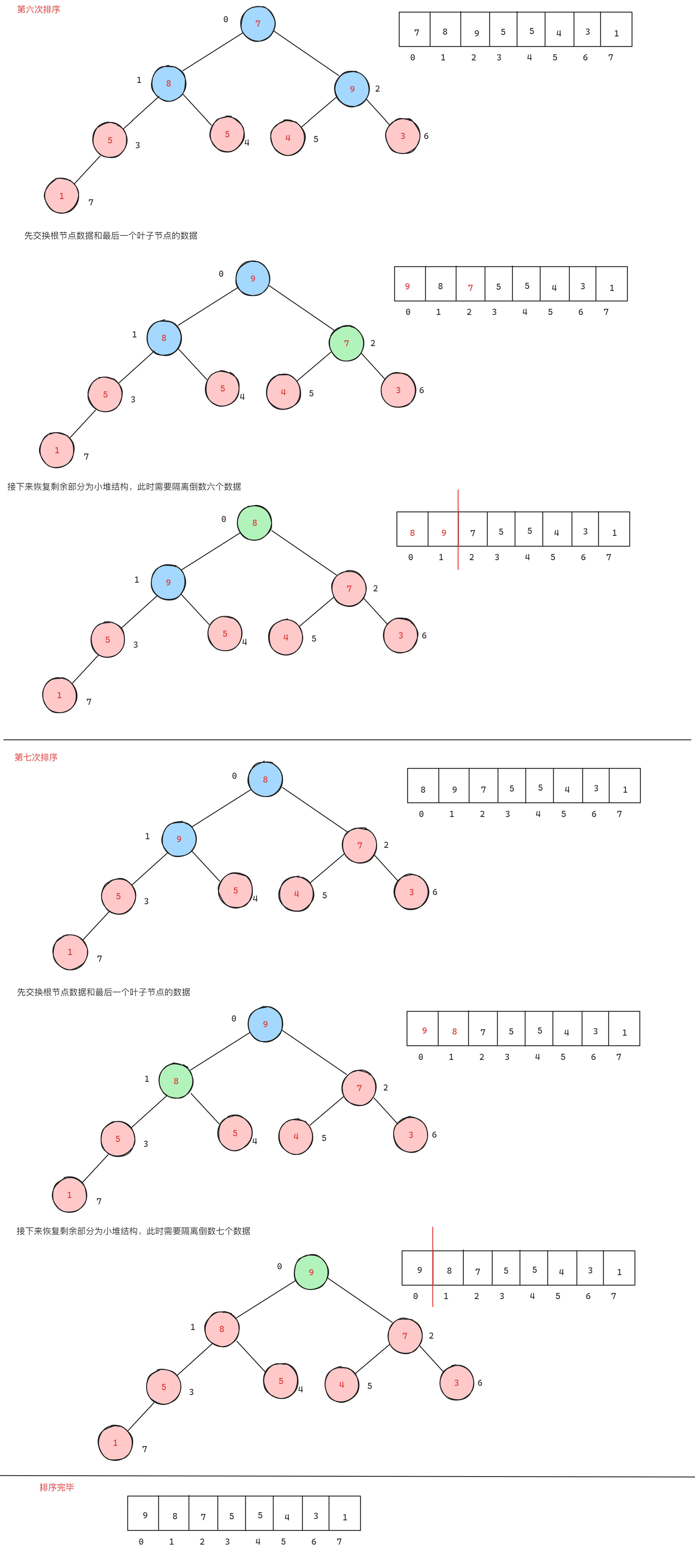
参考代码：

C
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
#define _CRT_SECURE_NO_WARNINGS 1

#include <stdio.h>

//交换函数
void swap(int* p1, int* p2)
{
    int tmp = *p1;
    *p1 = *p2;
    *p2 = tmp;
}

//向上调整算法
void AdjustUp(int* data, int child)
{
    int parent = (child - 1) / 2;
    while (child > 0)
    {
        if (data[child] < data[parent])
        {
            swap(&data[child], &data[parent]);
            child = parent;// 将孩子节点的下标改为之前的父亲节点的下标
            parent = (child - 1) / 2;// 再找出当前孩子的父亲节点的下标
        }
        else
        {
            break;
        }
    }
}

//向下调整算法
void AdjustDown(int* data, int sz, int parent)
{
    int child = parent * 2 + 1;
    while (child < sz)
    {
        if (child + 1 < sz && data[child] > data[child + 1])
        {
            child++;
        }
        if (data[child] < data[parent])
        {
            swap(&data[child], &data[parent]);
            parent = child;
            child = parent * 2 + 1;
        }
        else
        {
            break;
        }
    }
}

int main()
{
    int data[] = { 7,8,3,5,1,9,5,4 };
    //int data[] = { 35,70,56,90,60,25 };
    //常规的堆排序思路：创建堆并实现堆的插入和删除功能，再实现排序
    //优化的堆排序思路：通过向上/向下调整算法直接在原始数组上进行修改
    int sz = sizeof(data) / sizeof(int);
    //使用向上调整算法将数组中的数据转换成小堆结构
    for (int i = 0; i < sz; i++)
    {
        //对数组中的数据依次进行向上调整
        AdjustUp(data, i);// 使用变量i控制数组的数据获取
    }

    //使用向下调整算法对数组中的数据进行排序
    for (int i = sz - 1; i >= 0; i--)
    {
        //先交换根节点数据和最后一个叶子节点数据
        swap(&data[0], &data[i]);
        AdjustDown(data, i, 0);// 使用变量i控制数组的长度变化，注意i - 1是数组的下标
    }

    for (int i = 0; i < sz; i++)
    {
        printf("%d ", data[i]);
    }

    return 0;
}
输出结果：
9 8 7 5 5 4 3 1

同理可得，使用大堆排序时在不打印的情况下会得到升序结果，如果是打印则为降序结果

优化：向下调整建堆+向下调整排序（小堆为例）

向下调整建堆采用分组进行调整，先调整最后一个父亲节点为大堆，再依次向前调整其他子树，最后到根节点的调整，具体过程如下

参考代码：

C
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#define _CRT_SECURE_NO_WARNINGS 1

#include <stdio.h>

//交换函数
void swap(int* p1, int* p2)
{
    int tmp = *p1;
    *p1 = *p2;
    *p2 = tmp;
}

//向下调整算法
void AdjustDown(int* data, int sz, int parent)
{
    int child = parent * 2 + 1;
    while (child < sz)
    {
        if (child + 1 < sz && data[child] > data[child + 1])
        {
            child++;
        }
        if (data[child] < data[parent])
        {
            swap(&data[child], &data[parent]);
            parent = child;
            child = parent * 2 + 1;
        }
        else
        {
            break;
        }
    }
}

int main()
{
    int data[] = { 7,8,3,5,1,9,5,4 };
    //int data[] = { 35,70,56,90,60,25 };
    //常规的堆排序思路：创建堆并实现堆的插入和删除功能，再实现排序
    //优化的堆排序思路：通过向上/向下调整算法直接在原始数组上进行修改
    int sz = sizeof(data) / sizeof(int);

    //使用分组向下调整将数组中的数据转换成小堆结构
    //以最后一个父亲节点为起点，因为最后一个节点的下标为sz - 1，而算父亲节点的公式为parent = (child - 1)/2
    //故循环变量的初始值为(sz - 1 - 1)/2，即(sz - 2) / 2
    for (int i = (sz - 2) / 2; i >= 0; i--)
    {
        AdjustDown(data, sz, i);
    }

    //使用向下调整算法对数组中的数据进行排序
    for (int i = sz - 1; i >= 0; i--)
    {
        //先交换根节点数据和最后一个叶子节点数据
        swap(&data[0], &data[i]);
        AdjustDown(data, i, 0);// 使用变量i控制数组的长度变化，注意i - 1是数组的下标
    }

    for (int i = 0; i < sz; i++)
    {
        printf("%d ", data[i]);
    }

    return 0;
}
输出结果：
9 8 7 5 5 4 3 1

两种算法对比分析

现在的新问题是，为什么使用向下分组调整建堆+向下调整排序算法会比向上插入调整建堆+向下调整排序算法更优，因为二者最后都是通过向下调整排序进行排序，所以主要分析建堆方法，从时间复杂度的角度分析过程如下：

对于向上插入调整建堆来说有下面的分析：

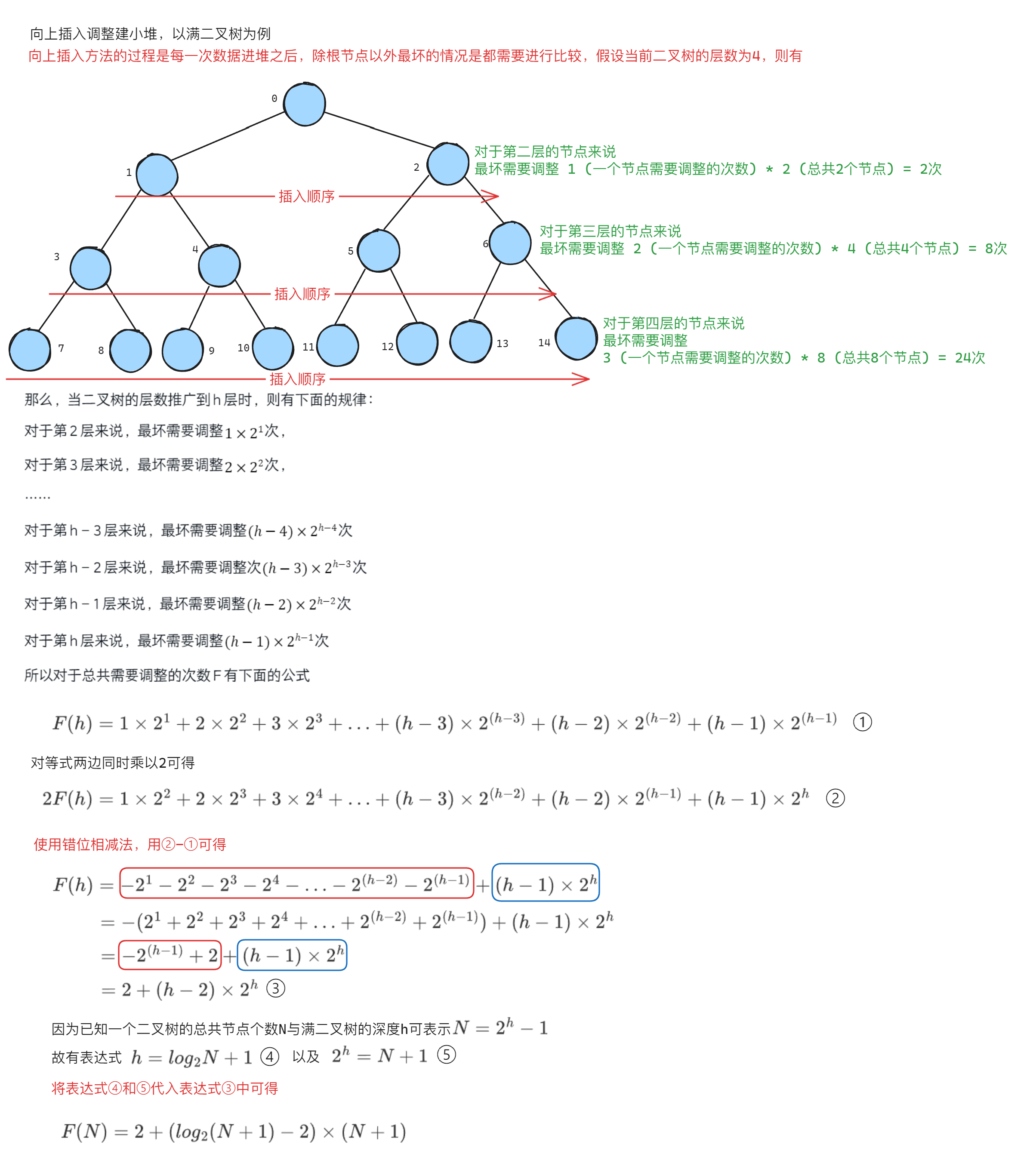
经过推导可知对于向上调整建堆的时间复杂度为\(O(Nlog_{2}{N})\)

对于向下分组调整建堆来说有下面的分析：

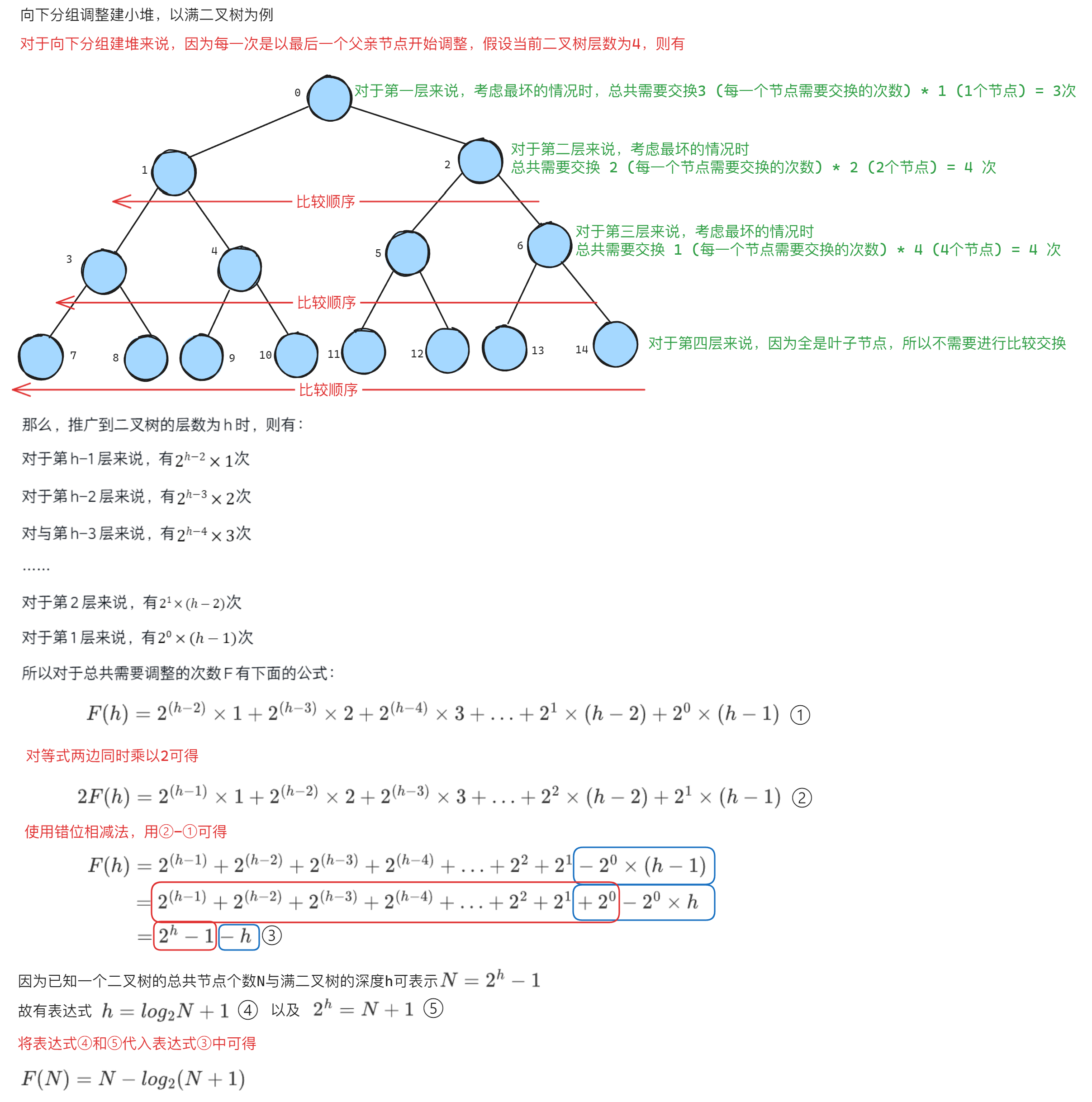
经过推导可知对于向下分组调整建堆的时间复杂度\(O(N)\)

综上所述，对比向上插入调整建堆来说，其时间复杂度要大于向下分组调整建堆，所以优先选择向下分组调整建堆+向下调整排序算法

因为向下调整排序算法的时间复杂度为\(O(Nlog_{2}{N})\)，故对于整个堆排序算法（向下分组调整建堆+向下调整排序）来说时间复杂度是\(O(Nlog_{2}{N})\)，并且堆排序算法不稳定

TopK问题

TopK问题思路分析

所谓TopK问题，在一组数据中找出前K个最大或者最小的数值，而使用TopK问题的解决思路的问题一般数据个数都比较大，如果直接用数组，则会导致数据无法一次性加载到内存从而难以比较，难者甚至因为数据过大只能存储到磁盘中，导致无法排列数据，而TopK的合理解决思路如下（此处以找前K个最大的数为例）：

整个数据很大，所以可能可以存储到内存中，也可能存储到磁盘中，所以不会一次性将磁盘中的数据全部加载到内存中进行管理

  1. 先抽取数据中的前K个值建立一个小堆，因为小堆的结构满足最小的数值一定在根节点，而比根节点大的数值一定会排在根节点的后面

  2. 再将剩余的N-K个数值依次与小堆的根节点数据进行比较，如果比根节点大就覆盖根节点并恢复成小堆

    Note

    此处的主要思路是：前K个最大数值肯定比原来整个数据中的其余数值都大，由于不需要保证在第一步中一定取出的是最大的数值，所以每一次遇到一个属于前K个最大数值的数据时肯定会顶替掉根节点进入小堆重新排列，此过程一直持续到最后没有数据比根节点（前K个最大的数值中的最小值）的数据还要大的时候就结束

  3. 当没有数据再进堆时，此时的小堆即为前K个最大的数值

图解思路

下面是过程示意图：

C
1
2
3
//以下面的数组为例
int data[] = { 111,333,89,22,45,276,4578,4673,2397,311,1231};
//假设需要取出最大的前5个数值

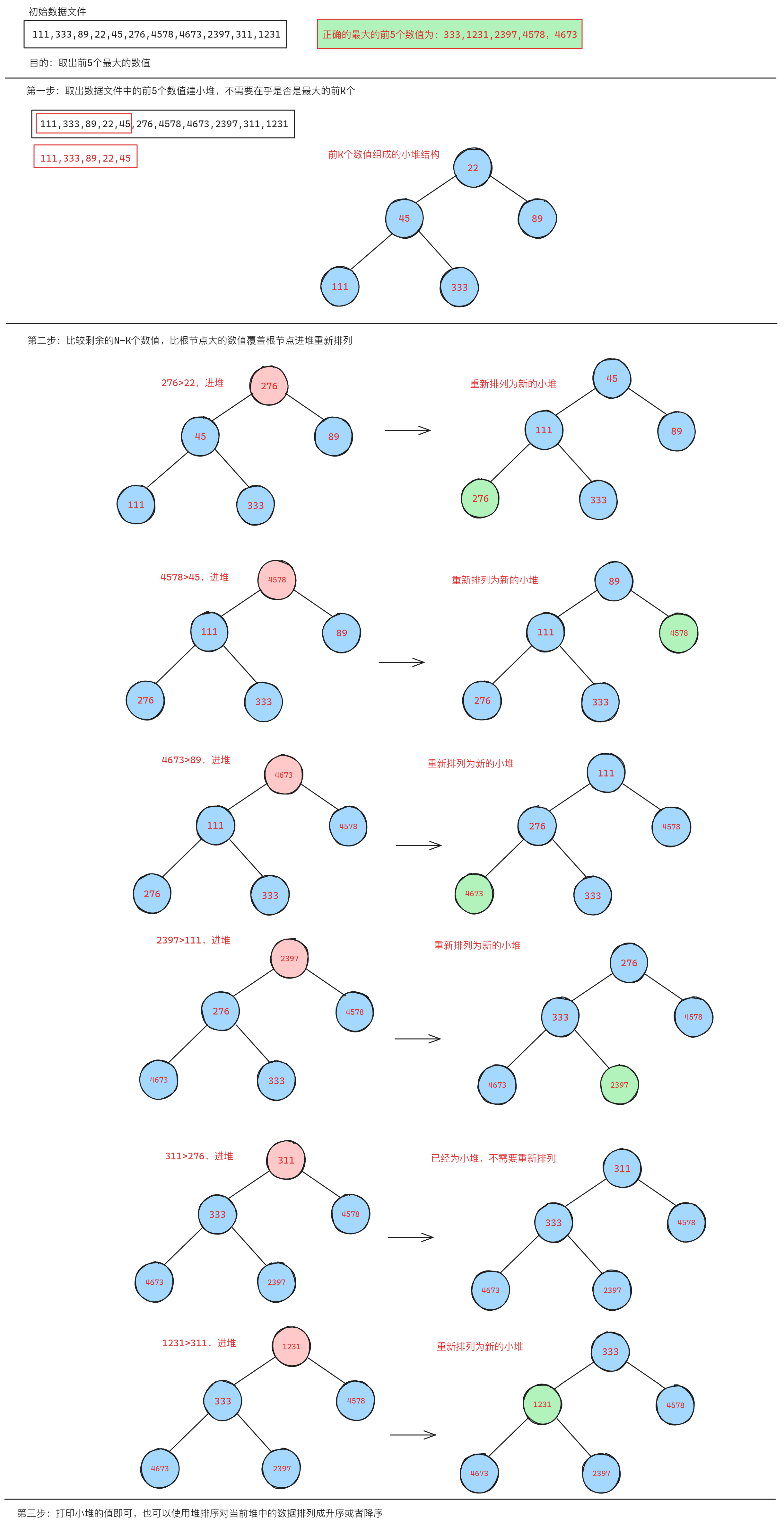
参考代码

C
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
#define _CRT_SECURE_NO_WARNINGS 1

#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
#include <time.h>

void swap(int* num1, int* num2)
{
    int tmp = *num1;
    *num1 = *num2;
    *num2 = tmp;
}

//向下调整算法
void AdjustDown(int* data, int sz, int parent)
{
    int child = parent * 2 + 1;
    while (child < sz)
    {
        if (child + 1 < sz && data[child] > data[child + 1]) 
        {
            child++;
        }
        if (data[child] < data[parent])
        {
            swap(&data[child], &data[parent]);
            parent = child;
            child = parent * 2 + 1;
        }
        else
        {
            break;
        }
    }
}

//向文件中写数据
void createData()
{
    //创建种子
    srand((unsigned int)time(0));
    //创建数据文件
    FILE* fin = fopen("data.txt", "w");
    assert(fin);
    //向文件中写数据
    int num = 10000;//数据个数
    for (int i = 0; i < num; i++)
    {
        int val = rand() % 10000;//生成10000以内的数据
        fprintf(fin, "%d\n", val);
    }

    fclose(fin);
}

//使用堆排序对小堆数据进行降序排序
void HeapSort(int* data, int sz)
{
    for (int i = sz - 1; i >= 0; i--)
    {
        swap(&data[0], &data[i]);
        AdjustDown(data, i, 0);
    }
}

//获取TopK数据
void printTopKnum(int k)
{
    //打开文件
    FILE* fout = fopen("data.txt", "r");
    //取出前K个数值建立小堆
    int* arr = (int*)malloc(sizeof(int) * k);
    assert(arr);
    //从文件中读数据放入数组中
    for (int i = 0; i < k; i++)
    {
        fscanf(fout, "%d", &arr[i]);
    }

    //建立小堆
    for (int i = (k - 2)/2; i >= 0; i--)
    {
        AdjustDown(arr, k, i);
    }
    //比较剩余的N-K个数值
    while (!feof(fout))
    {
        int val = 0;
        fscanf(fout, "%d", &val);
        if (val > arr[0])
        {
            arr[0] = val;
            AdjustDown(arr, k, 0);
        }
    }
    fclose(fout);

    //使用堆排序对小堆数据进行升序排序
    HeapSort(arr, k);

    //打印小堆的数据
    for (int i = 0; i < k; i++)
    {
        printf("%d ", arr[i]);
    }
}

int main()
{
    //向文件中写数据
    createData();
    //获取TopK数据
    int k = 10;
    printTopKnum(k);

    return 0;
}