波兰表达式与逆波兰表达式
约 2681 个字 380 行代码 3 张图片 预计阅读时间 14 分钟
前缀表示法(波兰表达式)
波兰表示法(英语:Polish notation,或波兰记法)是一种逻辑、算术和代数表示方法,其特点是操作符置于操作数的前面,因此也称做前缀表示法。如果操作符的元数是固定的,则语法上不需要括号仍然能被无歧义地解析。波兰记法是波兰数学家扬·武卡谢维奇于1920年代引入的,用于简化命题逻辑。
表达“三加四”时,前缀记法写作“+ 3 4 ”,而不是“3 + 4”。在复杂的表达式中,操作符仍然在操作数的前面,但操作数可能是包含操作符的平凡表达式。 例如,中缀运算式(5 - 6) * 7 ,在前缀表达式中可以表示为:
*(− 5 6) 7
或省略括号:
* - 5 6 7
由于简单的算术运算符都是二元的,该前缀表达式无需括号,且表述是无歧义的。在前面的例子里,中缀形式的括号是必需的,如果将括号移动到:
5 - (6 * 7)
即:
5 - 6 * 7
则会改变整个表达式的值。而其正确的前缀形式是:
- 5 * 6 7
减法运算要等它的两个操作数(5;6和7的乘积)都完成时才会处理。在任何表示法中,最里面的表达式最先运算,而在波兰表达式中,决定“最里面”的是顺序而不是括号。
中缀表达法
中缀表示法(或中缀记法)是一个通用的算术或逻辑公式表示方法, 操作符是以中缀形式处于操作数的中间(例:3 + 4)。与前缀表达式(例:+ 3 4 )或后缀表达式(例:3 4 + )相比,中缀表达式不容易被电脑解析逻辑优先顺序,但仍被许多程序语言使用,因为它符合大多数自然语言的写法。
与前缀或后缀记法不同的是,中缀记法中括号是必需的。计算过程中必须用括号将操作符和对应的操作数括起来,用于指示运算的次序。
后缀表达法(逆波兰表达式)
逆波兰表示法(英语:Reverse Polish notation,缩写RPN,或波兰记法、逆卢卡西维茨记法),是一种由波兰数学家扬·卢卡西维茨于1920年引入的数学表达式形式,在逆波兰记法中,所有操作符置于操作数的后面,因此也被称为后缀表示法、后序表示法[1]。逆波兰记法不需要括号来标识操作符的优先级。
逆波兰结构由弗里德里希·L·鲍尔和艾兹格·迪科斯彻在1960年代早期提议用于表达式求值,以利用堆栈结构减少计算机内存访问。逆波兰记法和相应的算法由澳大利亚哲学家、计算机学家查尔斯·伦纳德·汉布尔在1960年代中期扩充[2][3]。
在1960和1970年代,逆波兰记法广泛地被用于台式计算器,因此也在普通公众(如工程、商业和金融等领域)中使用。
下面大部分是关于二元运算,一个一元运算使用逆波兰记法的例子是阶乘的记法。
逆波兰记法中,操作符置于操作数的后面。例如表达“三加四”时,写作“3 4 + ”,而不是“3 + 4”。如果有多个操作符,操作符置于第二个操作数的后面,所以常规中缀记法的“3 - 4 + 5”在逆波兰记法中写作“3 4 - 5 + ”:先3减去4,再加上5。使用逆波兰记法的一个好处是不需要使用括号。例如中缀记法中“3 - 4 * 5”与“(3 - 4)5”不相同,但后缀记法中前者写做“3 4 5 * - ”,无歧义地表示“3 (4 5 ) -”;后者写做“3 4 - 5 * ”。
逆波兰表达式的解释器一般是基于堆栈的。解释过程一般是:操作数入栈;遇到操作符时,操作数出栈,求值,将结果入栈;当一遍后,栈顶就是表达式的值。因此逆波兰表达式的求值使用堆栈结构很容易实现,并且能很快求值。
注意:逆波兰记法并不是简单的波兰表达式的反转。因为对于不满足交换律的操作符,它的操作数写法仍然是常规顺序,如,波兰记法“/ 6 3”的逆波兰记法是“6 3 /”而不是“3 6 /”;数字的数位写法也是常规顺序
后缀表达式转前缀和中缀表达式
前缀表达式可以用二叉树的前序遍历得到,中缀表达式可以用二叉树的中序遍历得到,后缀表达式可以用二叉树的后序遍历得到。在转换过程中,始终以操作符作为根节点
例如,对于中缀表达式:
(1 + 2) * (3 + 4)
对应的二叉树为
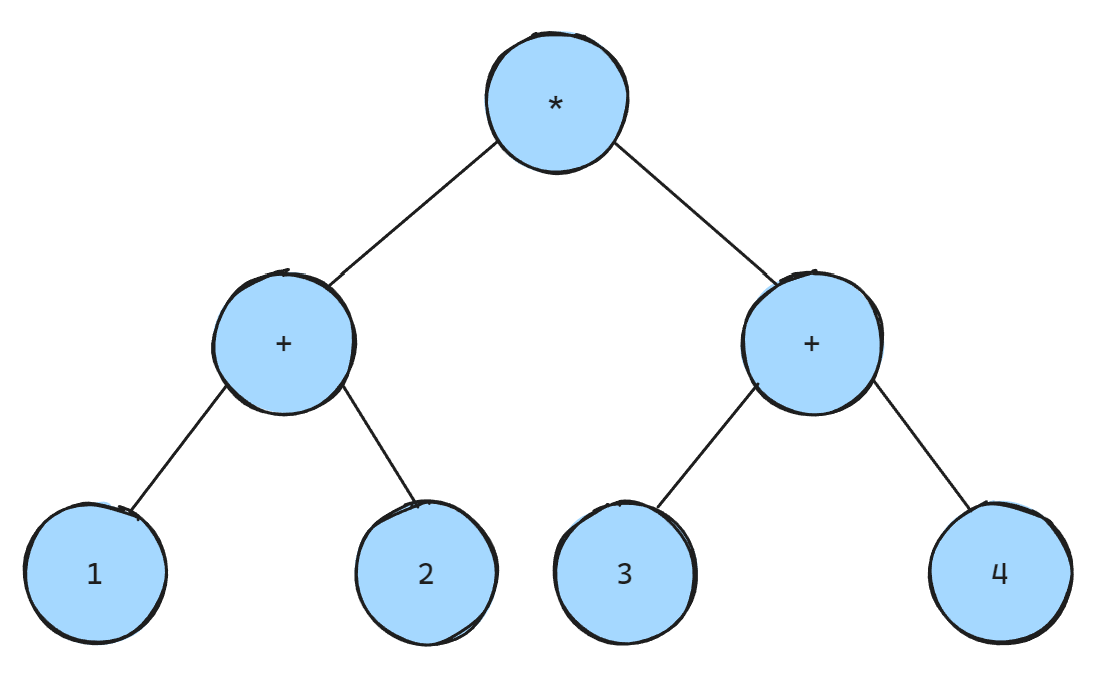
将其转化为前缀表达式为
* + 1 2 + 3 4
将其转化为后缀表达式为
1 2 + 3 4 + *
练习:逆波兰表达式求值
题目链接:150. 逆波兰表达式求值 - 力扣(LeetCode)
问题描述:
Quote
给你一个字符串数组tokens,表示一个根据逆波兰表示法表示的算术表达式。
请你计算该表达式。返回一个表示表达式值的整数。
注意:
- 有效的算符为
'+'、'-'、'*'和'/'。 - 每个操作数(运算对象)都可以是一个整数或者另一个表达式。
- 两个整数之间的除法总是向零截断。
- 表达式中不含除零运算。
- 输入是一个根据逆波兰表示法表示的算术表达式。
- 答案及所有中间计算结果可以用32 位整数表示。
示例 1:
| C++ |
|---|
| 输入:tokens = ["2","1","+","3","*"]
输出:9
解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
|
示例 2:
| C++ |
|---|
| 输入:tokens = ["4","13","5","/","+"]
输出:6
解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
|
示例 3:
| C++ |
|---|
| 输入:tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
输出:22
解释:该算式转化为常见的中缀算术表达式为:
((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
|
思路解析:
对于逆波兰表达式一般用栈的数据结构解决,当表达式中的字符为操作数时,操作数入栈,当表达式中的字符为操作符时,依次弹出两个操作数进行对应的算术运算。注意弹出的第一个数是操作符右侧的数,第二次弹出的数是操作符左侧的数,对于减法和除法需要注意运算顺序
使用C语言及栈来解决时,需要注意下面的问题:
- 因为题目给的运算式是单个字符串,在比较时需要使用到
strcmp函数,而不是直接使用==进行判断 - 因为
*的ASCII值小于其余三个运算符,并且数字可能存在负数,所以在处理减号不入栈时需要处理负数的情况 - 设计栈时,可以直接使用实际实现的栈数据结构,也可用一个空数组来模拟栈
使用C++来解决时,需要注意下,C++代码中如果使用atoi函数需要将原始的string字符串转换成C类型的字符串,否则atoi将无法使用
参考代码:
| C |
|---|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132 | // 使用C语言和栈解决问题
// 栈的声明
typedef int STDataType;
typedef struct stack
{
STDataType* data;
int top; // 栈顶位置
int capacity; // 元素个数
} ST;
// 栈的初始化
void STInit(ST* st);
// 栈的销毁
void STDestroy(ST* st);
// 数据入栈
void STPush(ST* st, STDataType x);
// 数据出栈
void STPop(ST* st);
// 判断栈是否为空
bool STEmpty(ST* st);
// 获取栈元素
STDataType STTop(ST* st);
// 栈的实现
// 栈的初始化
void STInit(ST* st)
{
// 判断是否存在队列
assert(st);
// 初始化队列
st->data = NULL;
st->top = 0; // 栈顶指针指向存储数据的下一个位置,代表栈内无数据
// st->top = -1;//栈顶指针指向存储数据的位置,代表栈内无数据
st->capacity = 0;
}
// 栈的销毁
void STDestroy(ST* st)
{
// 确保有栈的存在
assert(st);
// 销毁栈
free(st->data);
st->data = NULL;
st->top = st->capacity = 0;
}
// 数据入栈
void STPush(ST* st, STDataType x)
{
// 确保有栈的存在
assert(st);
// 向top位置增加数据,并使top向后移动
// 需要判断栈的容量大小
if (st->top == st->capacity)
{
// 如果栈的空间为0,则开辟四个空间,如果栈容量不为0,则扩容原来容量的2倍
int newCapacity = st->capacity == 0 ? 4 : st->capacity * 2;
STDataType* tmp = (STDataType*)realloc(st->data, sizeof(STDataType) * newCapacity);
assert(tmp);
st->data = tmp;
st->capacity = newCapacity;
}
// 数据压栈并改变top
st->data[st->top++] = x;
}
// 数据出栈
void STPop(ST* st)
{
// 确保有栈的存在
assert(st);
// 确保栈不会越界
assert(!STEmpty(st));
// 直接移动top指针,“看不见即删除”
st->top--;
}
// 判断栈是否为空
bool STEmpty(ST* st)
{
// 确保有栈的存在
assert(st);
// 栈为空返回真,栈不为空返回假
return st->top == 0; // 判断表达式返回值只有1和0,如果为真返回1(true),如果为假返回0(false)
}
// 获取栈元素
STDataType STTop(ST* st)
{
// 确保栈存在
assert(st);
// 确保栈不为空
assert(!STEmpty(st));
// top为栈内数据的下一个位置,要获取当前位置的元素需要-1操作
return st->data[st->top - 1];
}
int evalRPN(char** tokens, int tokensSize)
{
ST st;
STInit(&st);
for (int i = 0; i < tokensSize; i++)
{
//当遇到操作数时进栈
if (((strcmp(tokens[i], "+") > 0) + (strcmp(tokens[i], "-") >= 0 && atoi(tokens[i]) < 0) + (strcmp(tokens[i], "*") > 0) + (strcmp(tokens[i], "/") > 0)) > 2)
STPush(&st, atoi(tokens[i]));
else
{
//当遇到操作符时出栈运算
int num1 = STTop(&st);
STPop(&st);
int num2 = STTop(&st);
STPop(&st);
if (strcmp(tokens[i], "+") == 0)
STPush(&st, (num2 + num1));
if (strcmp(tokens[i], "-") == 0)
STPush(&st, (num2 - num1));
if (strcmp(tokens[i], "*") == 0)
STPush(&st, (num2 * num1));
if (strcmp(tokens[i], "/") == 0)
STPush(&st, (num2 / num1));
}
}
int ans = STTop(&st);
STPop(&st);
return ans;
}
|
| C++ |
|---|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38 | class Solution
{
public:
int evalRPN(vector<string>& tokens)
{
stack<int> st;
for(auto& val : tokens)
{
//不是操作符进行入栈操作
if(val != "+" && val != "-" && val != "*" && val != "/")
st.push(stoi(val));
//也可以写成下面的方式
//注意atoi接收的是C类型的字符串
//st.push(atoi(val.c_str()));
else
{
//当遇到操作符时取数值
int num1 = st.top();
st.pop();
int num2 = st.top();
st.pop();
//判断计算方式
if(val == "+")
st.push(num2 + num1);
else if(val == "-")
st.push(num2 - num1);
else if(val == "*")
st.push(num2 * num1);
else
st.push(num2 / num1);
}
}
int ret = st.top();
st.pop();
return ret;
}
};
|
| C++ |
|---|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35 | class Solution
{
public:
int evalRPN(vector<string>& tokens)
{
stack<int> st;
// 使用map和Lambda表达式对操作符和运算进行映射
map<string, function<int(int, int)>> m
{
{"+", [](int a, int b){return a + b;}},
{"-", [](int a, int b){return a - b;}},
{"/", [](int a, int b){return a / b;}},
{"*", [](int a, int b){return a * b;}}
};
for(auto& str : tokens)
{
if(m.count(str))
{
// 操作符取出操作数计算
int right = st.top();
st.pop();
int left = st.top();
st.pop();
// 使用包装器计算
int ans = m[str](left, right);
st.push(ans);
}
else
st.push(stoi(str));
}
return st.top();
}
};
|
中缀表达式转后缀表达式(了解思路)
前面介绍了后缀表达式如何转中缀表达式,那么思考一下中缀表达式如何转后缀表达式
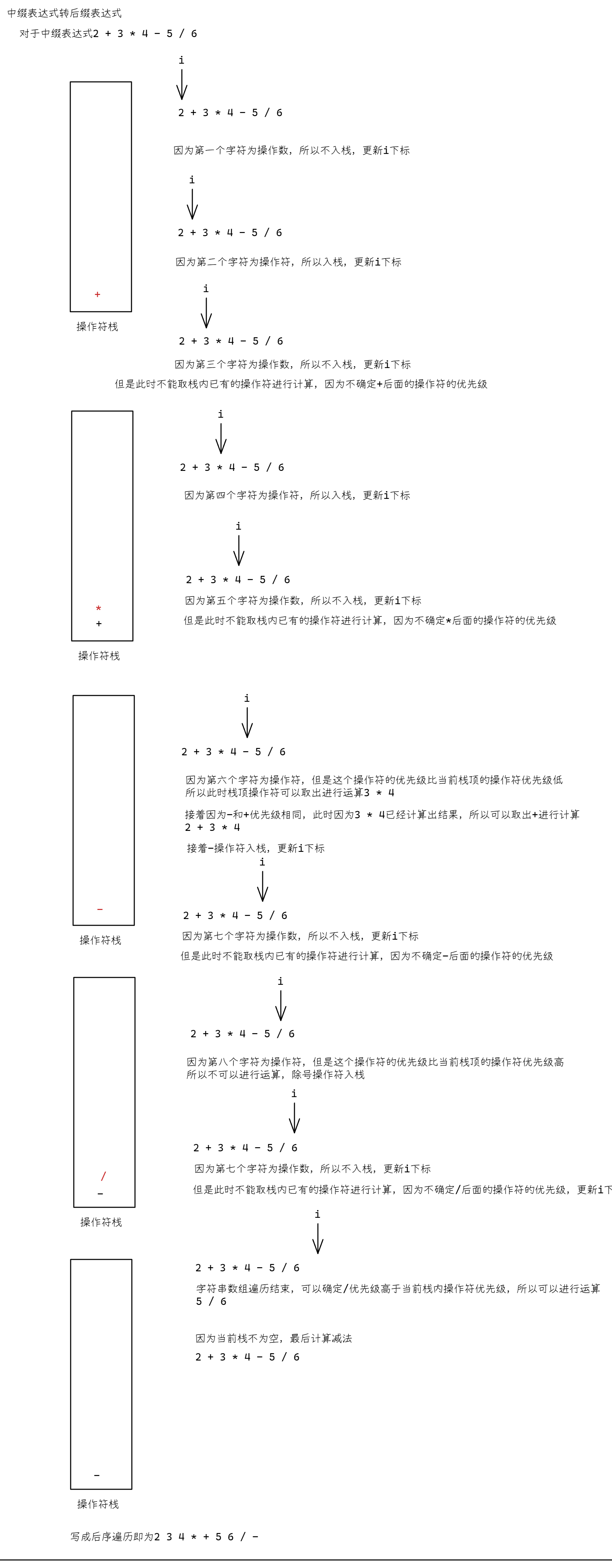
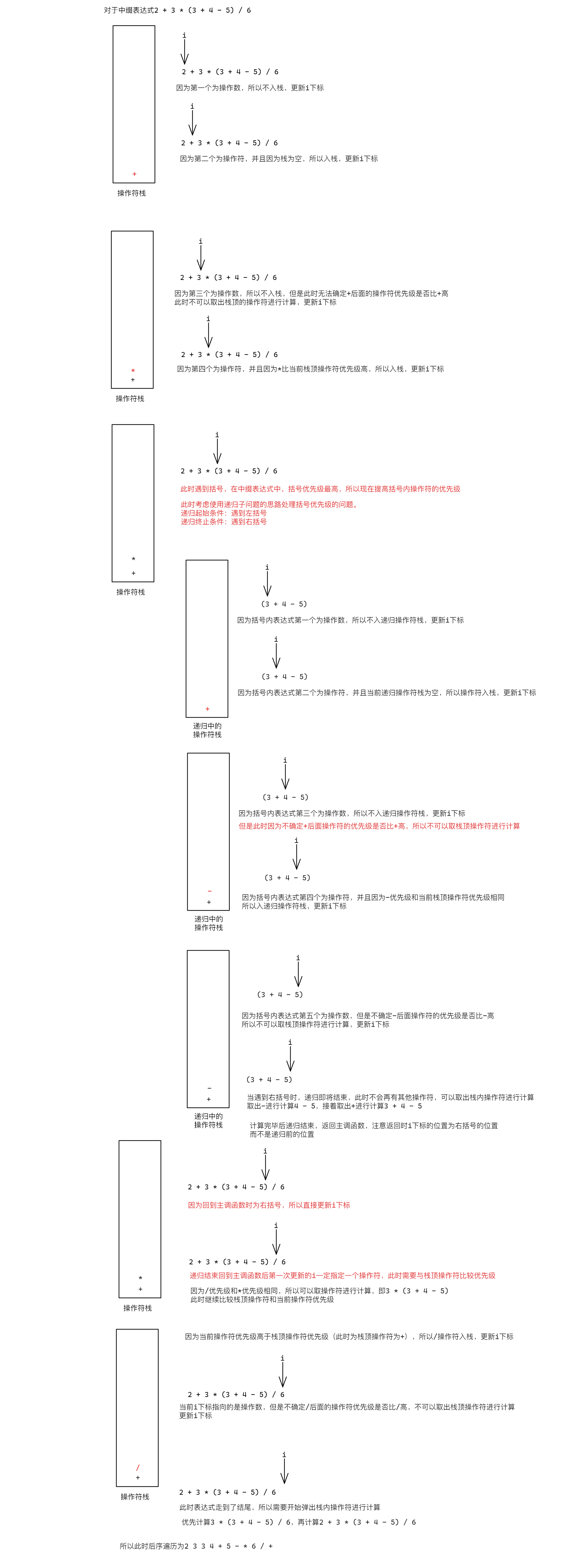
以下面的两个中缀表达式为例
-
不带括号的中缀表达式
2 + 3 * 4 - 5 / 6
-
带括号的中缀表达式
2 + 3 * (3 + 4 - 5) / 6
转后缀表达式基本思路与后缀表达式大体思路相反:
- 当遇到操作符时,操作符进栈
- 当遇到操作数时取操作符进行运算
但是需要考虑到下面的问题:
- 运算符优先级,什么时候该取操作符进行计算(不是单单遇到操作数就取操作符进行计算)
- 遇到括号需要提升优先级时应该如何处理
对于上面的两个问题提出两种解决方案:
- 处理运算符优先级时遵循两个原则
- 栈为空时,直接进操作符
- 栈不为空时,如果即将进入的操作符比当前栈内的操作符优先级高,那么就让该操作符进栈,而不是取操作符进行计算;如果即将进入的操作符比当前栈内的操作符优先级低或者相等,那么就可以让栈内当前操作符出栈进行计算,再让遇到的操作符进栈
- 遇到括号需要提升优先级可以采用递归子问题的方式解决,第一个原因是因为再递归中可以重现开辟一个栈,这个栈只需要存储当前括号内的操作符即可,第二个原因是因为括号内的表达式可以看作一个新的计算式,这个新的计算式也包括对应的运算符优先级,所以本质还是走第一个方案
具体分析如下图所示
Note
进行分析前的前置知识:
一个操作符的优先级不是由该操作符本身决定的,而应该是由相邻的操作符彼此直接优先级等级决定的。例如对于等式2+3*4,当计算时根据从左往右计算的规则,第一个看到的操作符是+,但是此时并不能进行计算,需要确定后面紧接的操作符是否比当前的+优先级高,很明显,*的优先级会高于+号,但是现在也不可以进行计算,因为*的操作符优先级的确比+高,但是并不确定紧挨着*的操作符的优先级是否比*高,接下来看*后面的操作符优先级,但是由于此时走到了算式结尾,所以现在可以确定*可以开始计算,当*计算完毕后则开始计算+
基本思路实现代码:
| C++ |
|---|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45 | class solution
{
public:
//获取当前运算符优先级
int getPriority(string& s1, string& top)
{
if ((s1 == "*" || s1 == "/") && (top == "+" || top == "-"))
return 1;
return 0;
}
//不带括号的中缀表达式转后缀表达式_直接打印后序遍历
void MiddleExpreToRpnNonbraces(vector<string>& v)
{
stack<string> s;
for (auto& str : v)
{
//操作符处理
if ((str == "/" || str == "*" || str == "-" || str == "+") && (s.empty() || getPriority(str, s.top())))
s.push(str);
else
{
//可能存在当前操作符优先级小于栈顶操作符,出一次操作符后的栈顶操作符可能和当前操作符优先级相同,判断不止一次不能用if
while (!s.empty() && (str == "/" || str == "*" || str == "-" || str == "+") && !getPriority(str, s.top()))
{
cout << s.top() << " ";
s.pop();
}
//如果出现优先级相同的时候可能栈内数据全部出完,此时需要重新进一次数据
if((str == "/" || str == "*" || str == "-" || str == "+") && s.empty())
s.push(str);
if (!(str == "/" || str == "*" || str == "-" || str == "+"))
cout << str << " ";
}
}
//栈内此时肯定还有操作符,所以需要依次弹出
while (!s.empty())
{
cout << s.top() << " ";
s.pop();
}
}
};
|
Tip
上面的思路为基本的思路,但是存在一种优化思路,因为不考虑括号时,一共就4个操作符,而这四个操作符只存在*和/比+和-优先级高,所以当前元素为*或/时即可取出进行计算
优化后的代码:
| C++ |
|---|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45 | class solution
{
public:
//获取当前运算符优先级
int getPriority(string& s1)
{
if (s1 == "*" || s1 == "/")
return 1;
return 0;
}
//不带括号的中缀表达式转后缀表达式_直接打印后序遍历
void MiddleExpreToRpnNonbraces(vector<string>& v)
{
stack<string> s;
for (auto& str : v)
{
//操作符处理
if ((str == "/" || str == "*" || str == "-" || str == "+") && (s.empty() || getPriority(str)))
s.push(str);
else
{
//可能存在当前操作符优先级小于栈顶操作符,出一次操作符后的栈顶操作符可能和当前操作符优先级相同,判断不止一次不能用if
while (!s.empty() && (str == "/" || str == "*" || str == "-" || str == "+") && !getPriority(str))
{
cout << s.top() << " ";
s.pop();
}
//如果出现优先级相同的时候可能栈内数据全部出完,此时需要重新进一次数据
if((str == "/" || str == "*" || str == "-" || str == "+") && s.empty())
s.push(str);
if (!(str == "/" || str == "*" || str == "-" || str == "+"))
cout << str << " ";
}
}
//栈内此时肯定还有操作符,所以需要依次弹出
while (!s.empty())
{
cout << s.top() << " ";
s.pop();
}
}
};
|
| C++ |
|---|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69 | class solution
{
public:
//获取当前运算符优先级
int getPriority(const string& s1, const string& top)
{
if (((s1 == "(" && (top == "*" || top == "/") && (top != "+" || top != "-")))
|| ((s1 == "(" && (top != "*" || top != "/") && (top == "+" || top == "-")))
|| (s1 != "(" && (s1 == "*" || s1 == "/") && (top == "+" || top == "-")))
return 1;
return 0;
}
//带括号的中缀表达式转后缀表达式_直接打印后序遍历
void MiddleExpreToRpn(vector<string>& v, size_t& i)
{
stack<string> s;
for (; i < v.size(); i++)
{
//处理操作符
if ((v[i] == "/" || v[i] == "*" || v[i] == "-" || v[i] == "+") && (s.empty() || getPriority(v[i], s.top())))
s.push(v[i]);
//当遇到左括号时
else if (v[i] == "(")//左括号进入递归操作符栈
{
i++;
//需要在递归中同时改变i的值
MiddleExpreToRpn(v, i);
}
//当遇到右括号时结束递归
else if (v[i] == ")")
{
//结束递归前需要对栈内操作符进行处理
while (!s.empty())
{
cout << s.top() << " ";
s.pop();
}
return;
}
else
{
//可能存在当前操作符优先级小于栈顶操作符,出一次操作符后的栈顶操作符可能和当前操作符优先级相同,判断不止一次不能用if
while (!s.empty() && (v[i] == "/" || v[i] == "*" || v[i] == "-" || v[i] == "+") && !getPriority(v[i], s.top()))
{
cout << s.top() << " ";
s.pop();
}
//如果出现优先级相同的时候可能栈内数据全部出完,此时需要重新进一次数据
if ((v[i] == "/" || v[i] == "*" || v[i] == "-" || v[i] == "+") && s.empty())
s.push(v[i]);
//可能存在一个操作符优先级高于当前栈顶的操作符
if ((v[i] == "/" || v[i] == "*" || v[i] == "-" || v[i] == "+") && (s.empty() || getPriority(v[i], s.top())))
s.push(v[i]);
if (!(v[i] == "/" || v[i] == "*" || v[i] == "-" || v[i] == "+"))
cout << v[i] << " ";
}
}
//栈内此时肯定还有操作符,所以需要依次弹出
while (!s.empty())
{
cout << s.top() << " ";
s.pop();
}
}
};
|


