二分查找算法¶
约 4784 个字 871 行代码 9 张图片 预计阅读时间 27 分钟
介绍¶
二分查找算法,是一种快速在一组有序且严格递增的区域中找一个指定元素的算法,其基本原理类似于猜数字游戏,先猜一个中间数值,再根据中间数值与目标值进行比较,判断目标值在中间值左侧部分还是右侧部分改变下一次猜的数值
Note
实际上,二分查找的本质是利用了「二段性」,所以只需要查找的区间可以根据某一种条件分为两个子区间,就可以使用二分查找算法,而不一定需要满足「有序且严格递增」
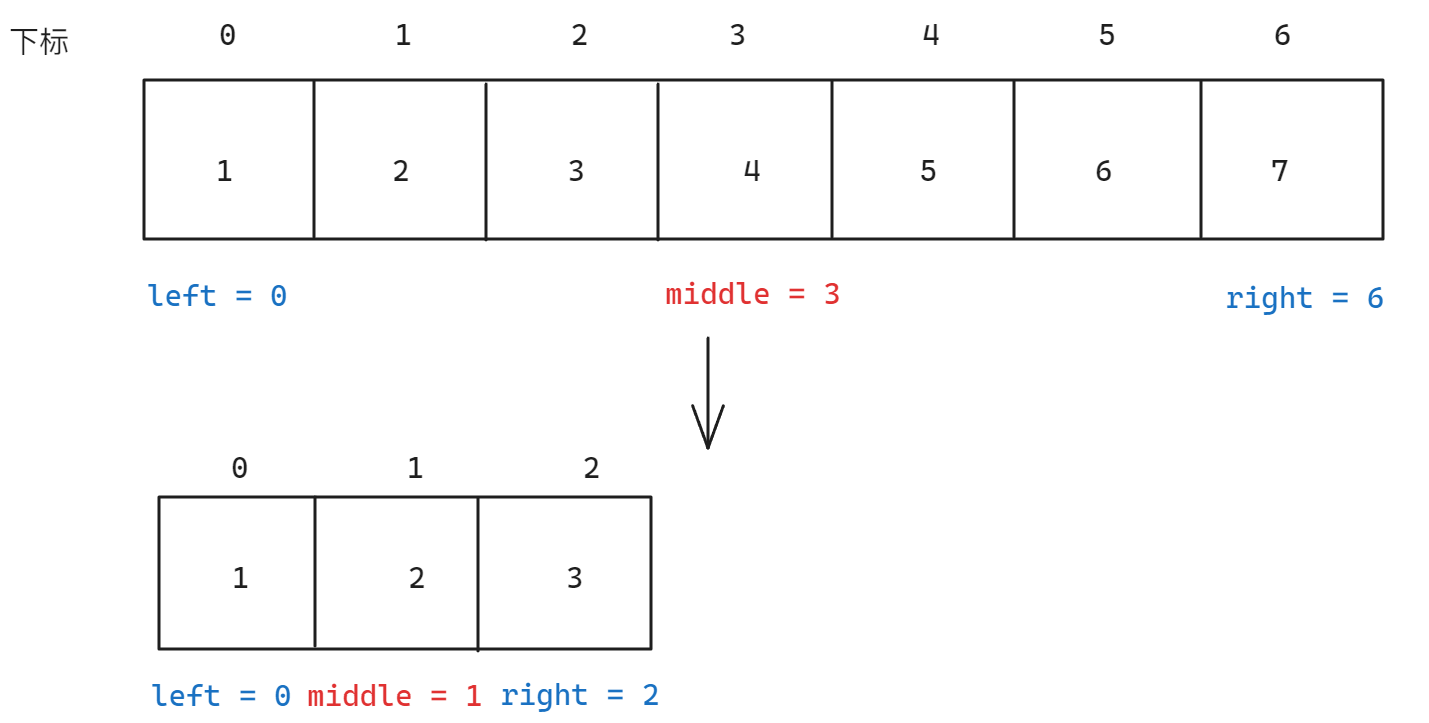
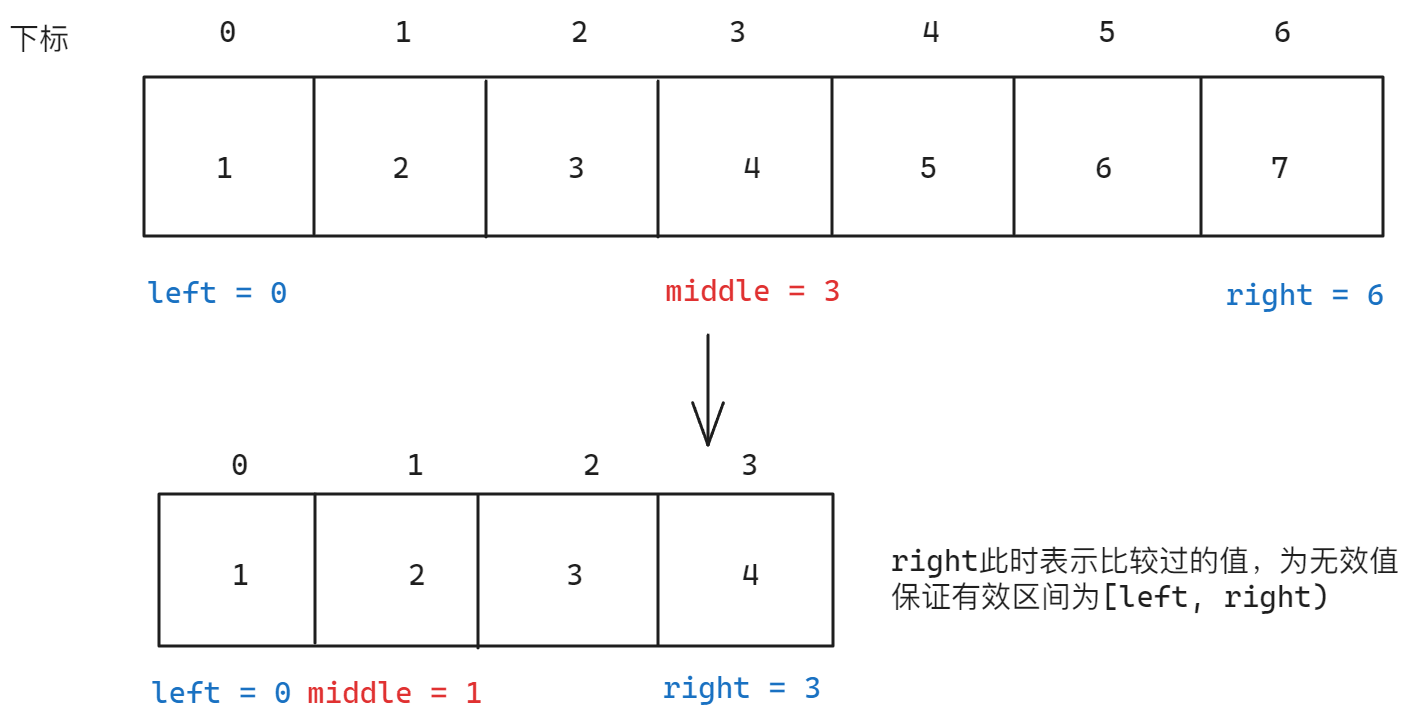
有了基本思路,根据前面的基本思路就需要进行代码实现,二分查找算法根据查找区间右侧端点是否包含分为两种情况,假设左侧端点为left,右侧端点为right:
- 左闭右闭区间:[
left,right],这种情况下最明显的特点就是left==right时是有效区间 - 左闭右开区间:[
left,right),这种情况下与左闭右闭区间刚好相反,当left==right时是无效区间
Info
所谓有效区间,代表该区间内的所有值都是有效可查找的,所以对于闭区间来说,当left==right时,也需要进行判断,因为当前值可能是结果,但是对于开区间来说,当left==right时,就不需要判断
因为接下来的查找一个循环进行的动作,而在整个循环中,必须保证left和right构成的区间必须与一开始设定的区间原则一致,例如开始为左闭右开区间,则在整个循环中,必须保证left和right构成的区间始终为左闭右开区间,这个左闭右开区间在整个过程中也被称为循环不变量
左闭右闭原则下,因为left和right都是有效值,所以下一次更新时,left和right对应的值也必须是未比较过的值(即有效值)
左闭右闭原则下,因为left是有效值,right是无效值,所以下一次更新时,left对应的值是未比较过的值(即有效值),right对应的值是比较过的值(即无效值)
代码实现:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 | |
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 | |
示例题目¶
Quote
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
| C++ | |
|---|---|
1 2 3 | |
示例 2:
| C++ | |
|---|---|
1 2 3 | |
提示:
- 你可以假设
nums中的所有元素是不重复的。 n将在[1, 10000]之间。nums的每个元素都将在[-9999, 9999]之间。
参考代码如下:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | |
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | |
Note
在使用二分查找算法的左闭右开区间逻辑时,需要注意计算中间值不可以使用left+(right - left + 1) / 2或者(left + right + 1) / 2,此时会导致mid和right指向同一个位置
在正常的比较逻辑下的mid是还未比较的数值(有效值),而right代表的是已经比较的数值(无效值),左闭右开区间中right更新到mid说明mid已经比较过而变为无效值
但是当前情况下,mid在未比较时就已经与right处于同一个位置导致左闭右开原则违背,所以左闭右开区间时计算中间值不可以使用left+(right - left + 1) / 2或者(left + right + 1) / 2
二分算法查找基本模板¶
这个版本的二分算法模板比较简单,所以也带来了比较强的局限性,简单了解即可
Warning
模板不是死记硬背的,切忌死记硬背
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 | |
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | |
二分查找算法查找端点模版¶
二分查找算法查找端点一般是一个结果区间的左右两个端点,本部分的模版需要根据二分查找算法的二段性进行区间划分,从而确定使用哪一种查找端点模版
Info
本模板的思路来自于力扣34题,具体分析见该题分析
Warning
模板不是死记硬背的,切忌死记硬背
Note
需要注意,不论是左闭右开区间,还是左闭右闭区间,最后返回的左端点和右端点分别是left和left-1,下面以左闭右开区间为例
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 | |
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 | |
相关题目¶
力扣35.搜索插入位置¶
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 | |
力扣69.x的平方根¶
问题描述:
Quote
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为\(O(\log_{2}{N})\)的算法。
示例 1:
| C++ | |
|---|---|
1 2 | |
示例 2:
| C++ | |
|---|---|
1 2 | |
示例 3:
| C++ | |
|---|---|
1 2 | |
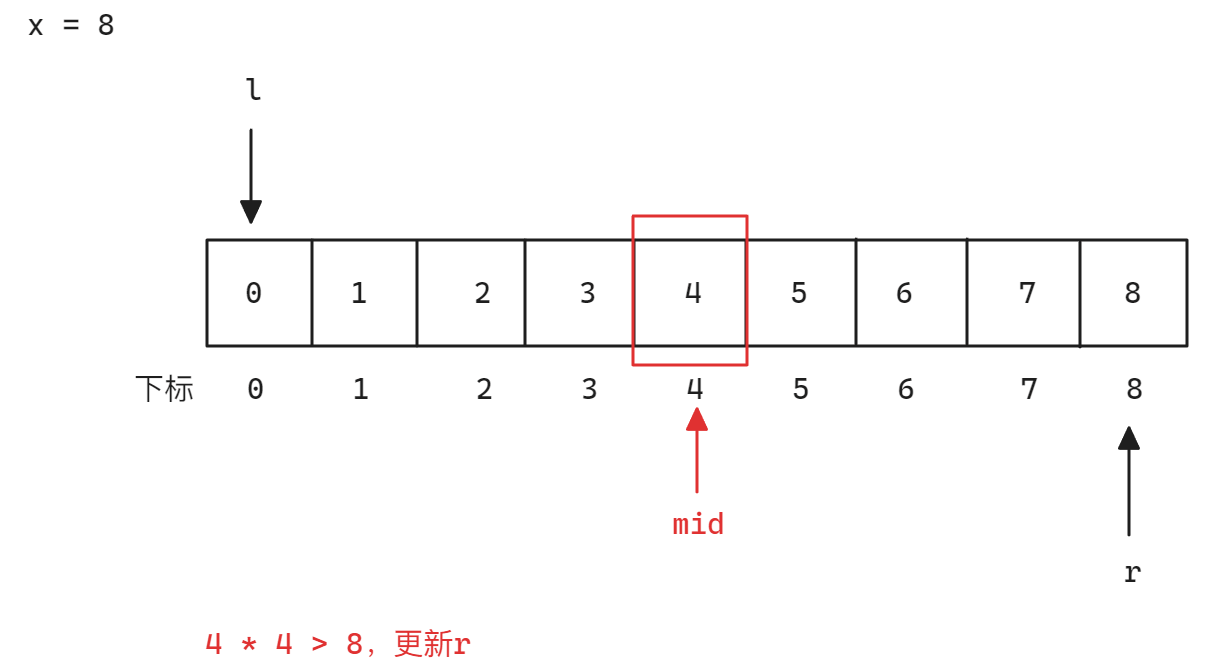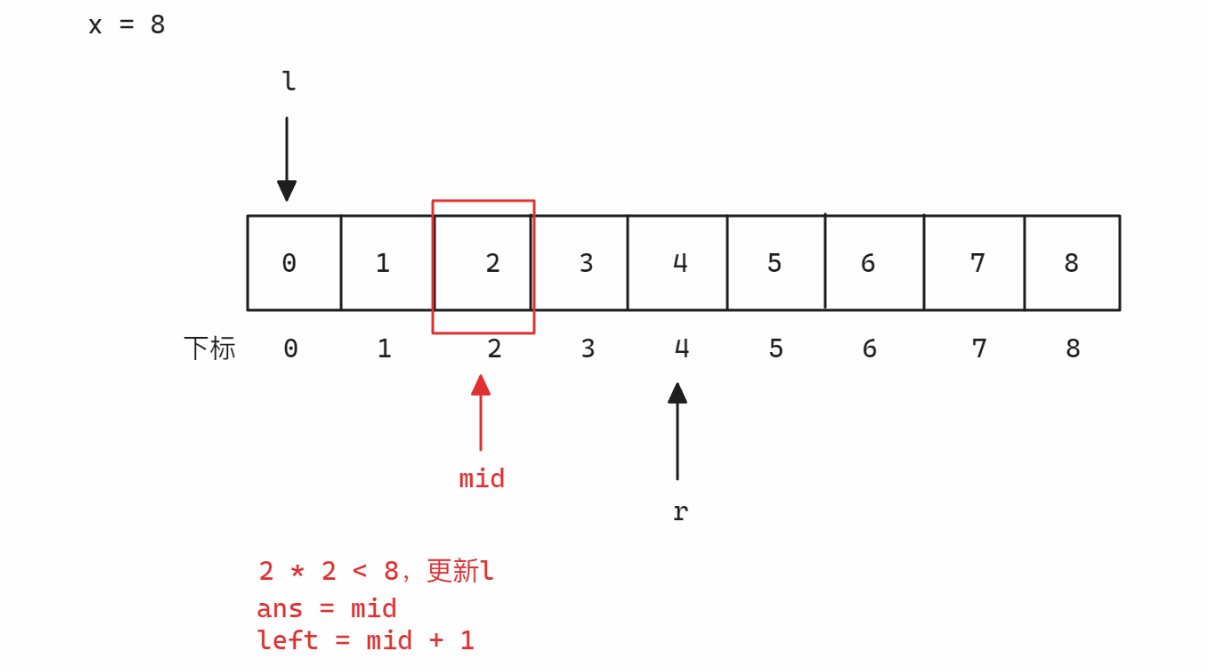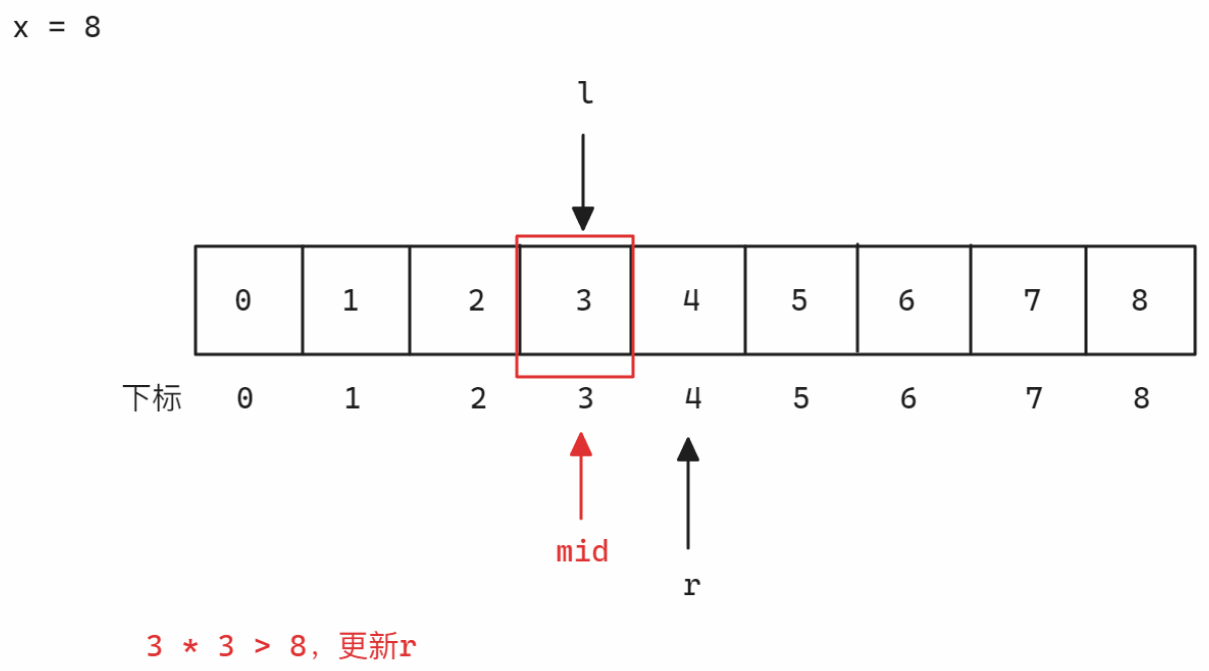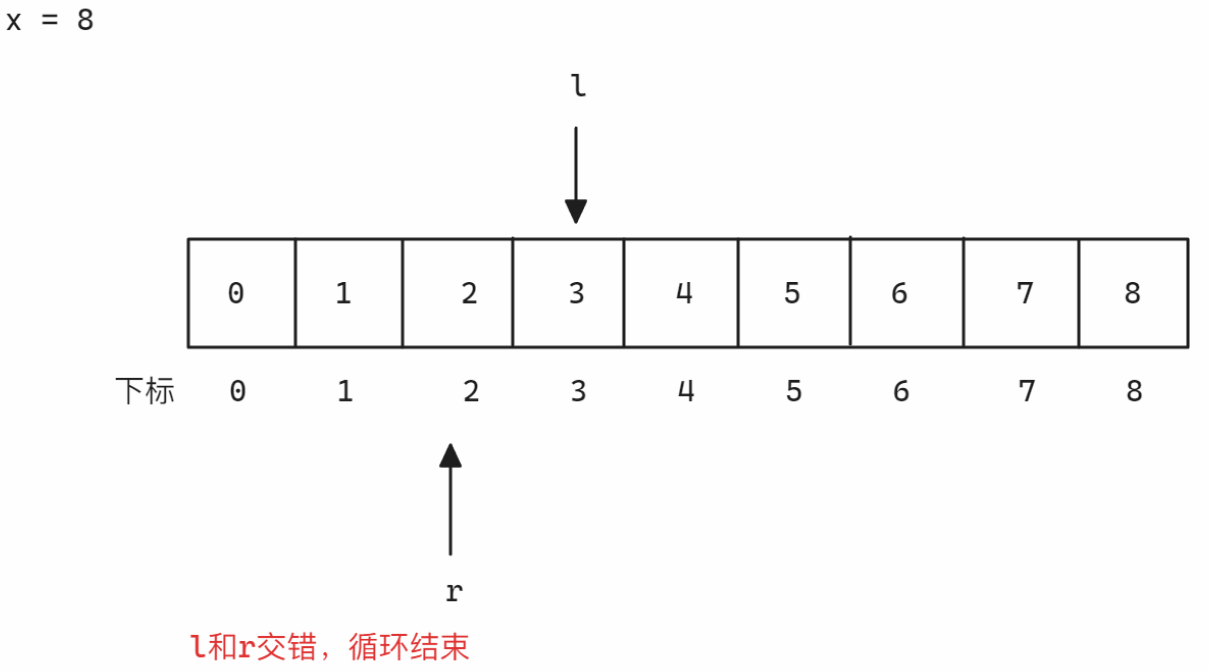
思路分析:
- 解法1:暴力解法 本题最直观的解法就是依次枚举,直到遇到枚举的数的平方值小于或者等于目标值,返回这个枚举的数值
-
解法2:二分查找 本题可以考虑依次枚举出小于等于
x的数值,但是比较时,不同于暴力解法,从枚举的过程中可以看到推出下面的规律:所以,根据上面的规律可以推出满足二段性的区间:1.
mid * mid <= x2.mid * mid > x
关键步骤:
为了保证最后可以记下满足条件的值并返回,在更新left之前,先对当前mid值进行记录
本题需要注意数值范围,小心越界问题,C语言/C++数据类型取值范围见表
示意图如下:
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 | |
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 | |
力扣367.有效的完全平方数¶
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | |
力扣34.在排序数组中查找元素的第一个和最后一个位置¶
问题描述:
Quote
给你一个按照非递减顺序排列的整数数组nums,和一个目标值target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值target,返回[-1, -1]。
你必须设计并实现时间复杂度为\(O(\log_{2}{N})\)的算法解决此问题。
示例 1:
| C++ | |
|---|---|
1 2 | |
示例 2:
| C++ | |
|---|---|
1 2 | |
示例 3:
| C++ | |
|---|---|
1 2 | |
思路分析:
- 解法1:暴力解法 本题暴力解法就是遍历数组,记录起始位置和终止位置
-
解法2:二分查找 题目提到数组是升序但非递减,所以直接找
target肯定结果不唯一,但是本题需要找的是第一个和最后一个位置对应的下标,所以可以考虑设定两个一定不存在的边界值,使用二分查找确定左右端点。因此可以根据是否是左右端点确定满足二段性的区间因为二分查找一次只能查找出一个值,所以左右端点需要分开进行查找,查找的方式有两种:
-
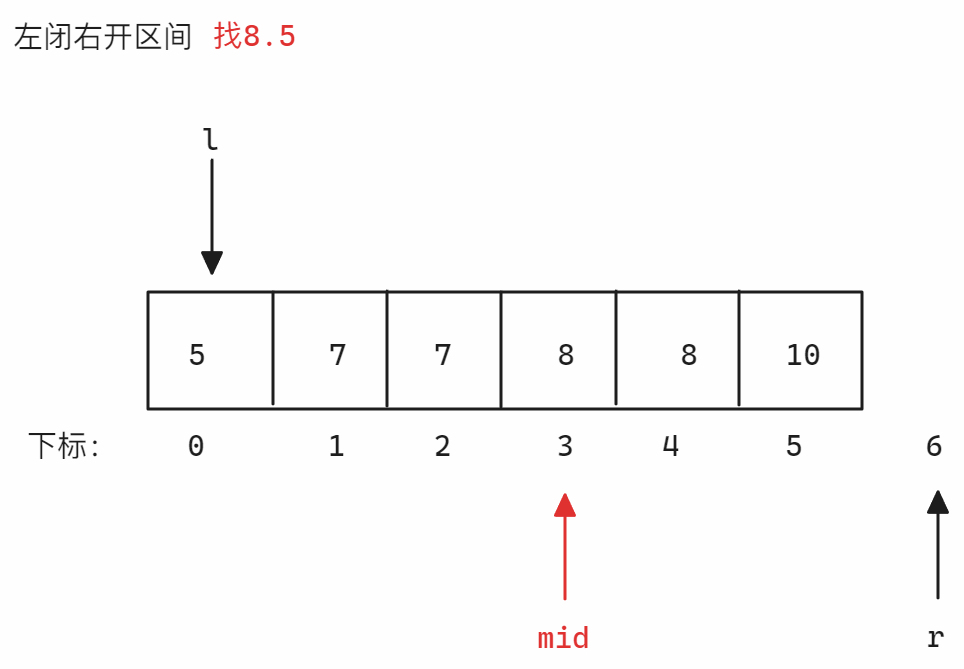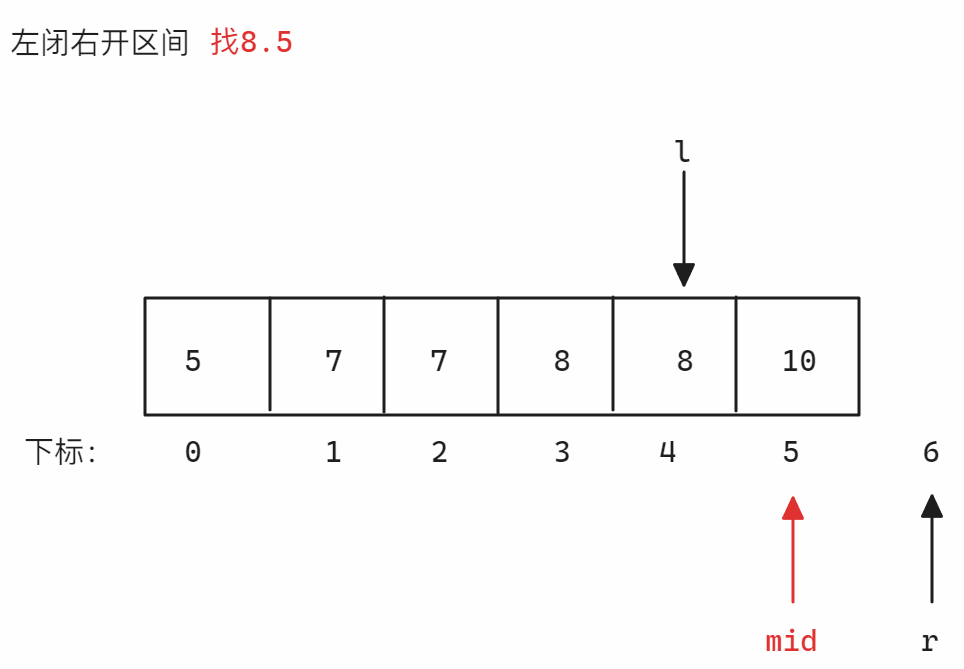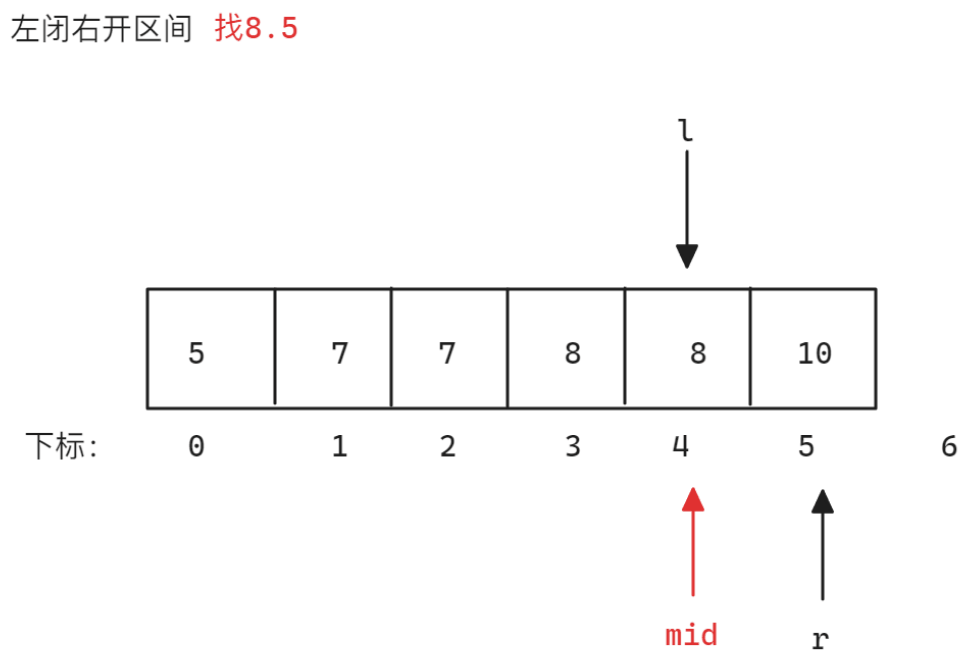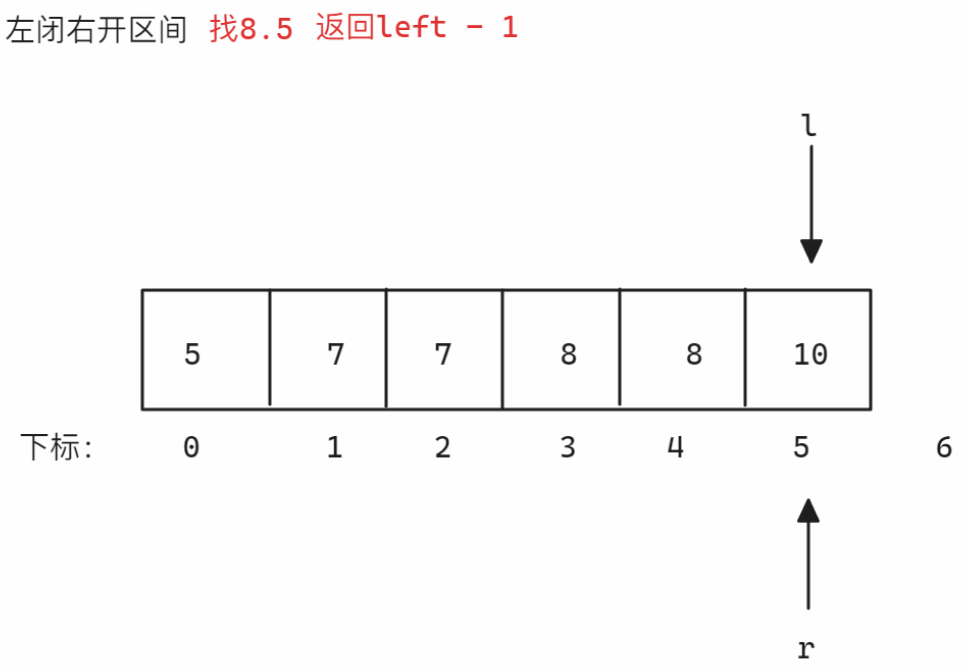
查找临界值,本题题干提到数组全是整数,所以一定不存在浮点数,假设找的数值是8,则可以考虑找8.5和7.5,这两个数值一定不存在于数组中,所以可以根据这两个值确定边界,以查找7.5和8.5为例,使用左闭右闭区间或左闭右开区间均是正确思路,因为这个思路本质是查找一个值,而不是确定端点
-
查找端点值:这个思路是直接利用二分查找算法找到左端点和右端点,但是不能通过直接的等于就判定一定是起点还是终点。判断如何划分出二段性区间,找这两个端点的思路基本一致,都是为了找一个边界值,所以二段性区间基本一致,对于左端点:找出区间:1. 小于左端点的值 2. 大于等于左端点的值,对于右端点:1. 小于等于右端点的值 2. 大于右端点的值
-
关键步骤:
不论是解法1还是解法2都需要判断target是否存在于nums中,否则会返回一个不存在的或者奇怪的区间,并且在判断是否存在之前一定要注意先判断是否包含越界情况
-
解法1示意图如下:
以
nums = [5,7,7,8,8,10],target = 8为例 -
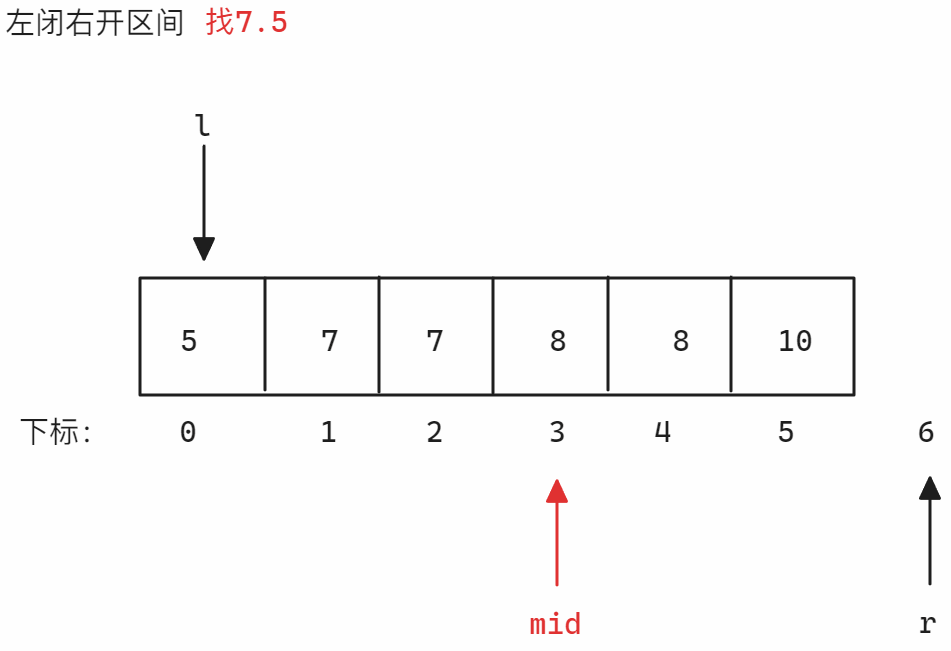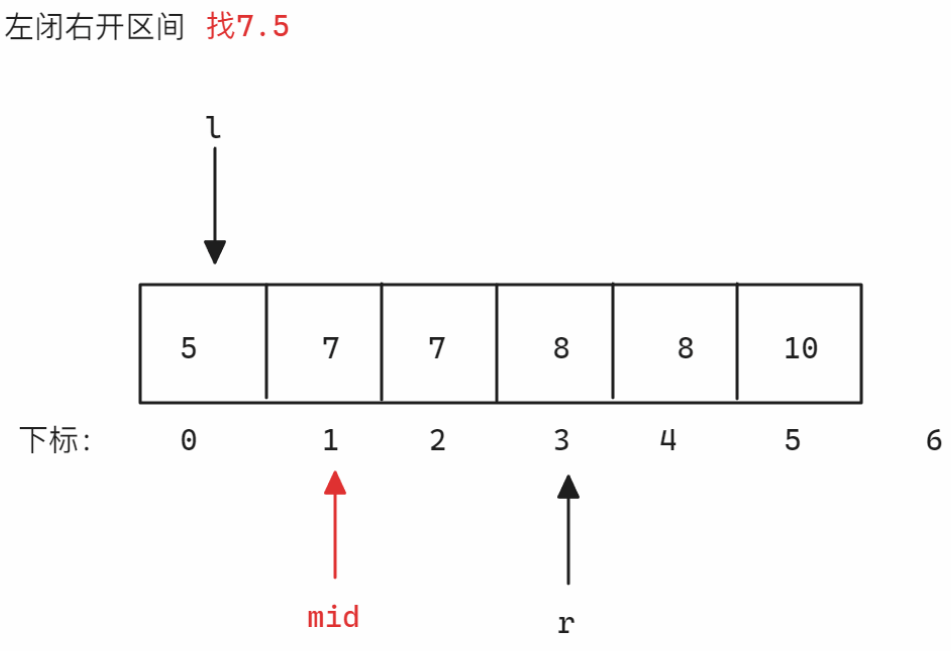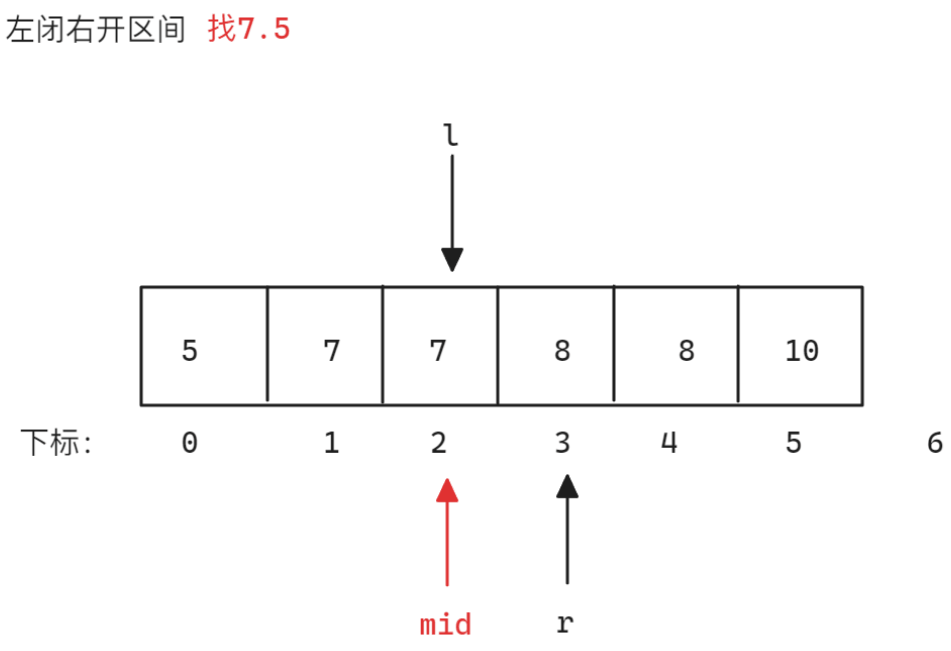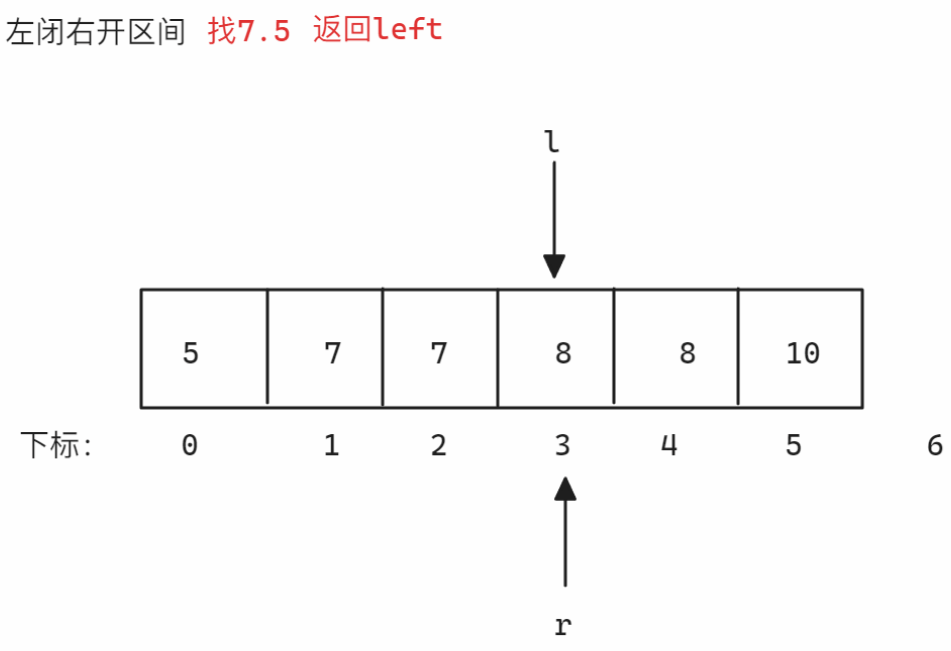
解法2示意图如下:
以
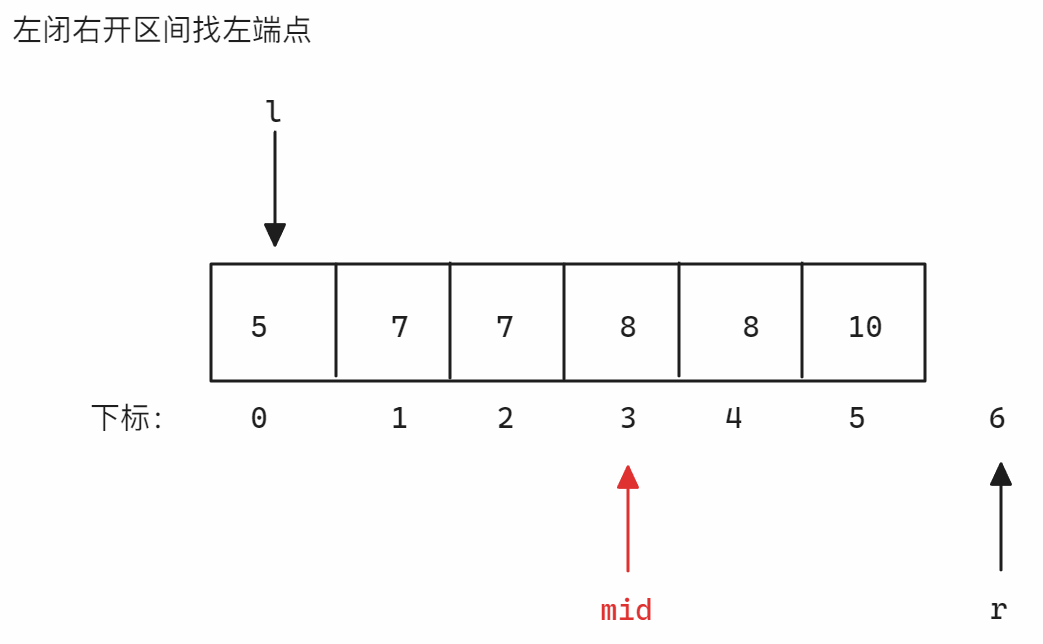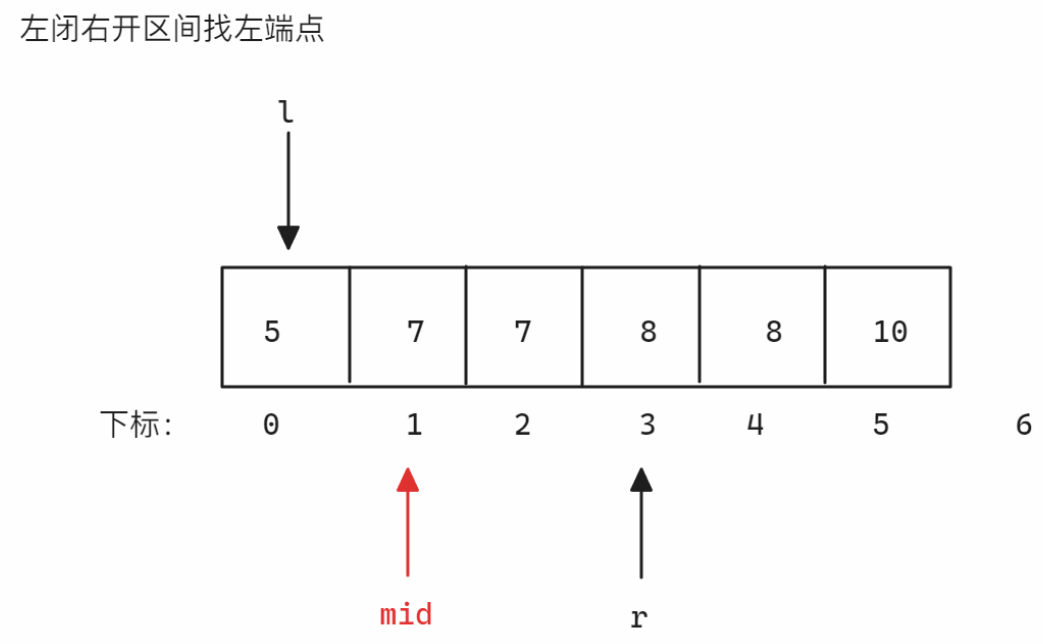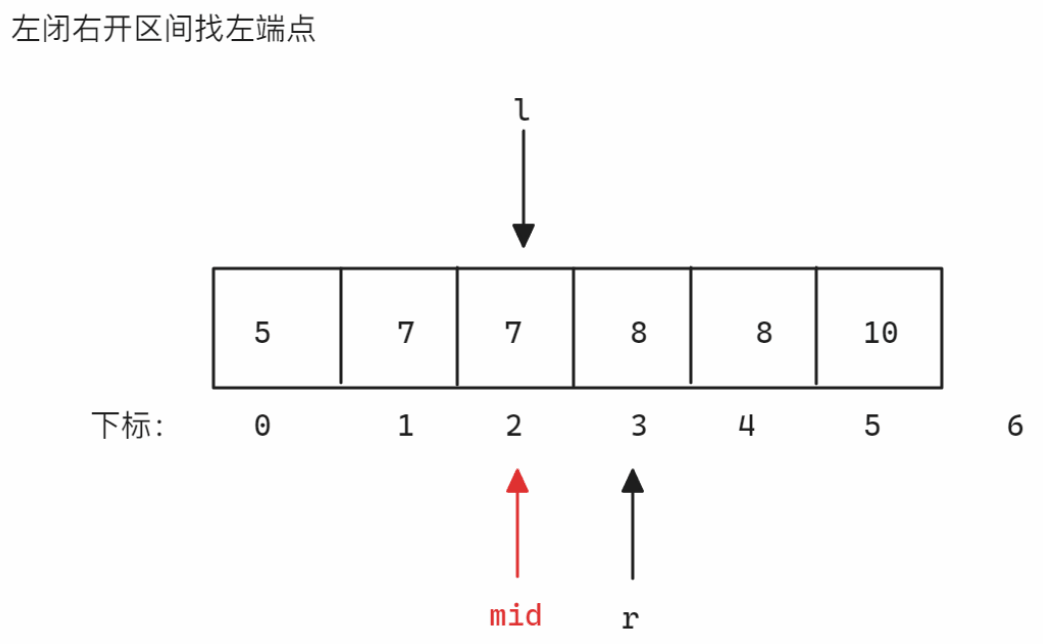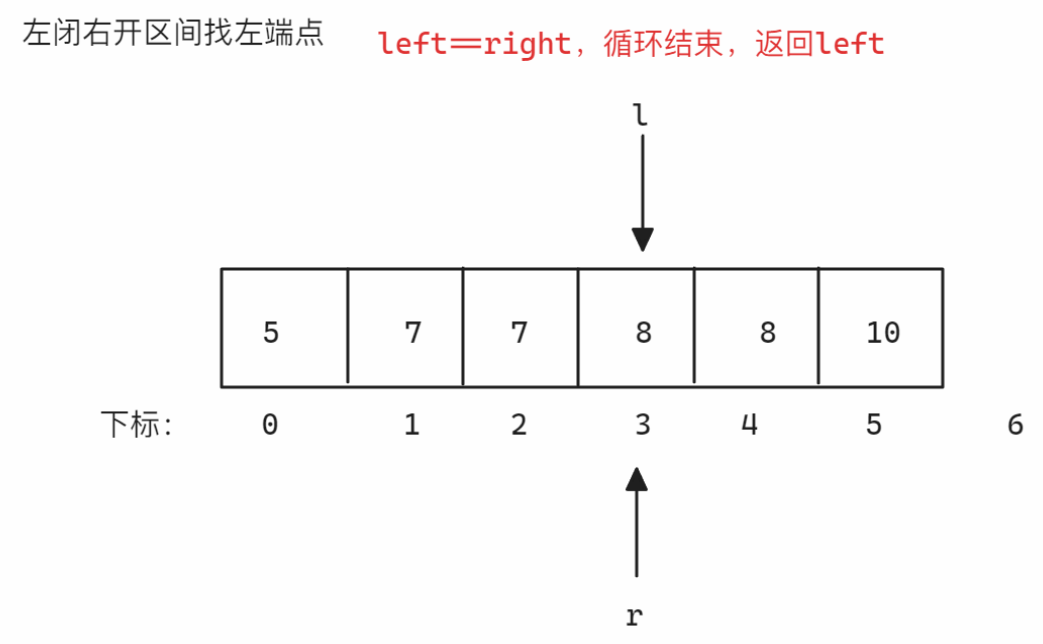
nums = [5,7,7,8,8,10],target = 8为例-
左闭右开区间找左端点 找左端点时划分的区间为
<8和>=8,当nums[mid]小于8时,因为要得到左端点,所以>=8的部分一定含有多个8,所以需要减小right位置从而减小区间,所以更新left,否则更新right,因为是左闭右开区间,所以当left和right相遇时[left, right)无效,结束寻找示意图如下:
-
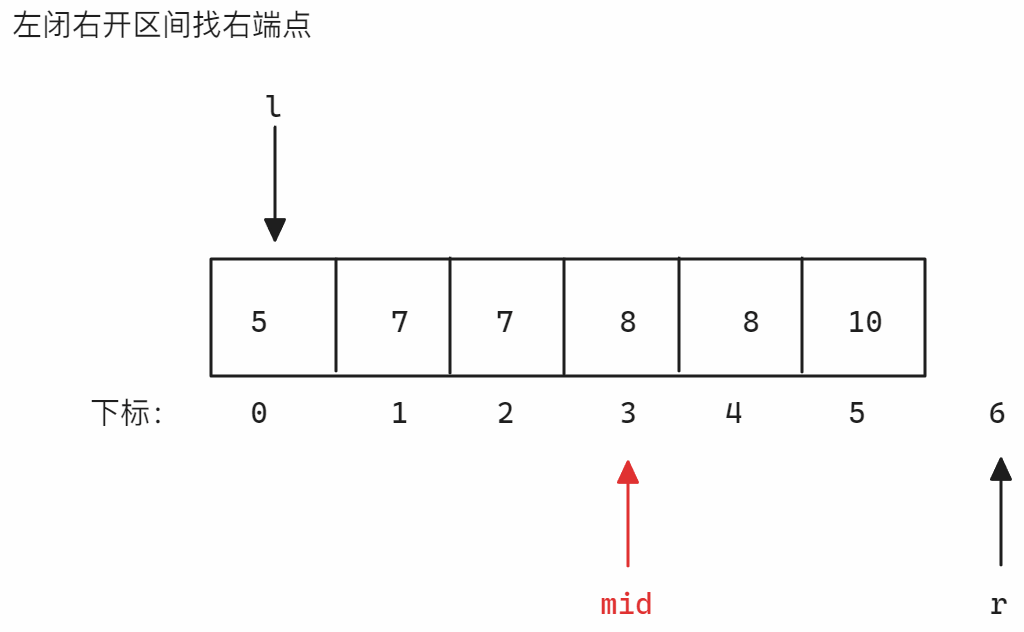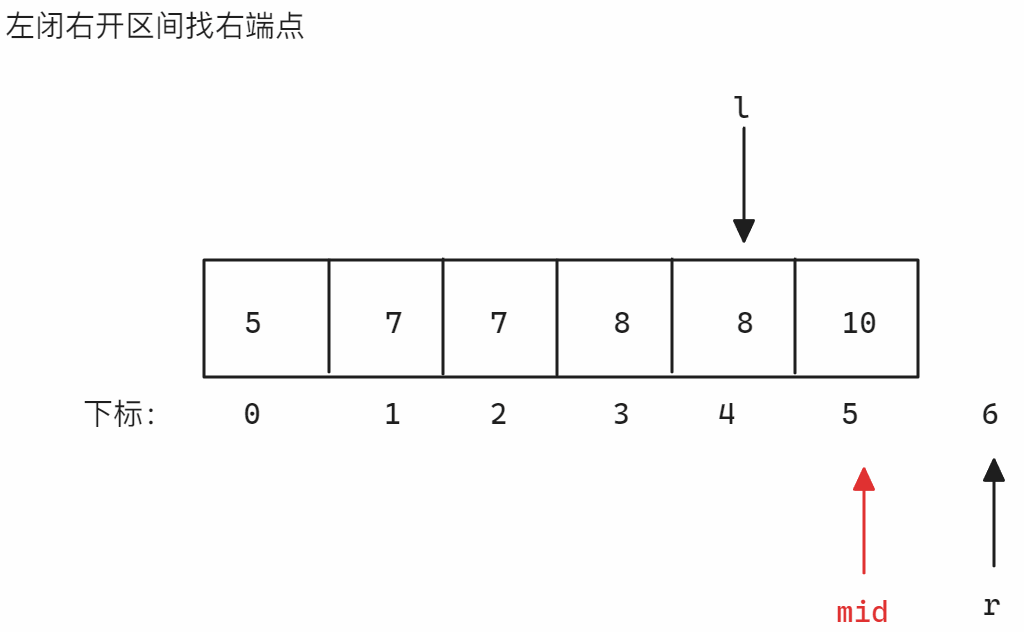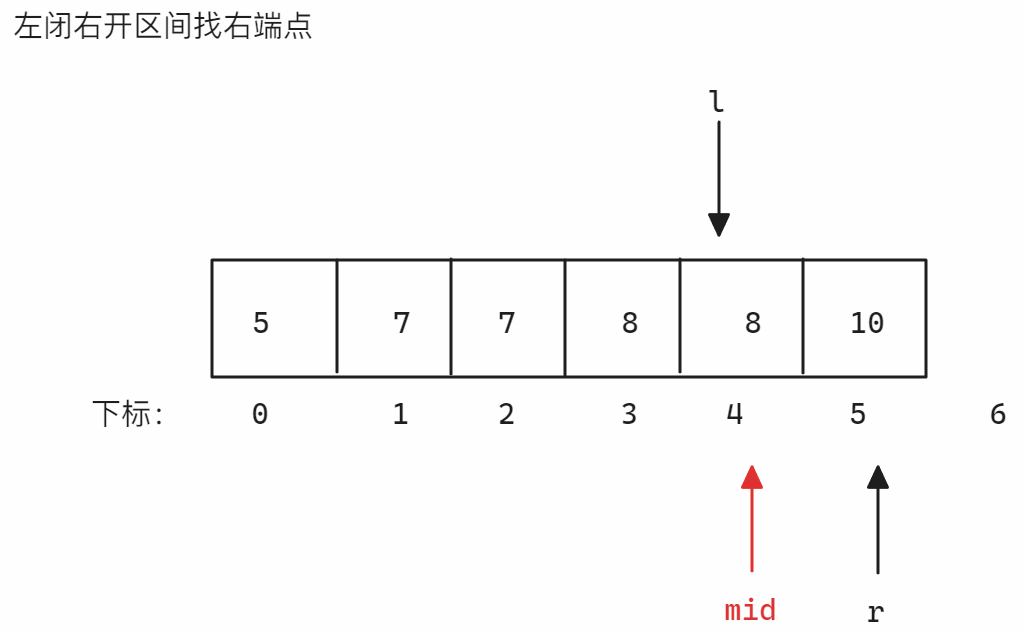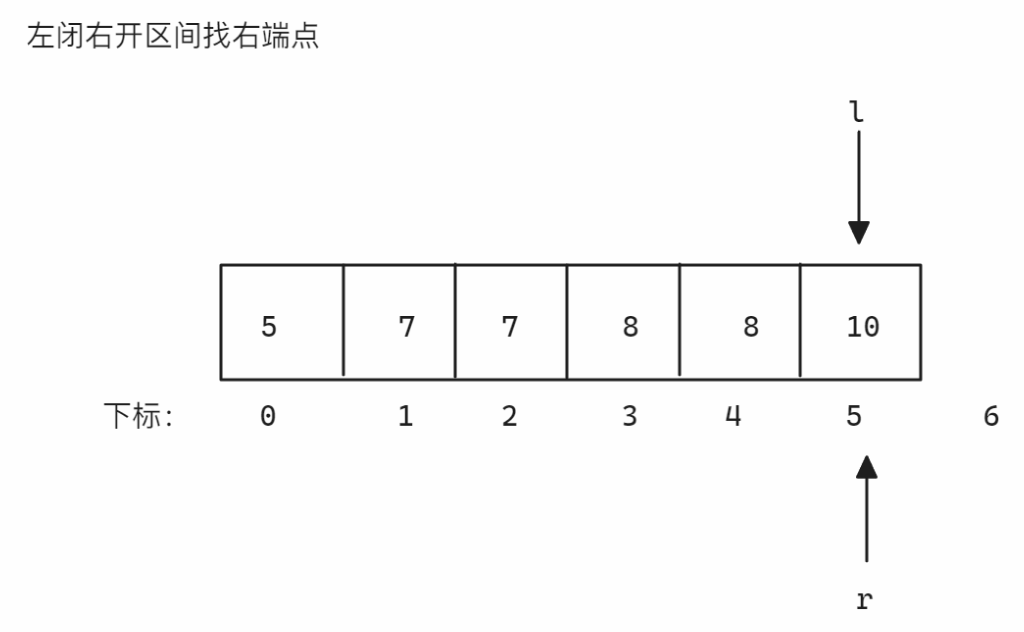
左闭右开区间找右端点 找右端点时划分的区间为
<=8和>8,当nums[mid]小于等于8时,因为要得到右端点,所以<=8的部分必须确保包含所有8,所以此时需要增加left从而扩大<=8区间,所以更新right,否则更新left,因为是左闭右开区间,所以当left和right相遇时[left, right)无效,结束寻找示意图如下:
-
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 | |
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 | |
牛客JZ53.数字在升序数组中出现的次数¶
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 | |
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 | |
力扣852.山脉数组的峰顶索引¶
问题描述:
Quote
给定一个长度为n的整数山脉数组arr,其中的值递增到一个峰值元素然后递减。
返回峰值元素的下标。
你必须设计并实现时间复杂度为\(O(\log_{2}{N})\)的解决方案。
示例 1:
| C++ | |
|---|---|
1 2 | |
示例 2:
| C++ | |
|---|---|
1 2 | |
示例 3:
| C++ | |
|---|---|
1 2 | |
思路分析:
- 解法1:暴力解法 本题的暴力解法很简单,只需要找到数组中的最大值即可,因为题目保证数组是一个山脉数组,并且根据题干描述「其中的值递增到一个峰值元素然后递减」,说明一定只存在一个峰值元素
- 解法2:二分查找 本题就是典型的二分查找应用于非有序且严格递增的区间,但是因为二分查找算法的本质是利用二段性,所以只需要在本题中找到二段性即可使用二分查找算法。本题的二段性可以分为两个区间:1. 左侧小于峰值 2. 右侧小于等于峰值,根据这个二段性区间,可以考虑选用找左侧端点模板
关键步骤:
本题并没有直接给出target,所以需要分析本题的target,根据题目描述「其中的值递增到一个峰值元素然后递减」,所以如果nums[mid]如果小于nums[mid + 1],则说明还没有遇到峰值,此时就需要更新left,否则更新right
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | |
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | |
力扣162.寻找峰值¶
问题描述:
Quote
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回任何一个峰值所在位置即可。
你可以假设nums[-1]=nums[n]=-∞。
你必须实现时间复杂度为\(O(\log_{2}{N})\)的算法来解决此问题。
示例 1:
| C++ | |
|---|---|
1 2 3 | |
示例 2:
| C++ | |
|---|---|
1 2 3 4 | |
思路分析:
-
解法1:暴力解法 本题暴力解法与上题暴力解法一致,因为题目提到「返回任何一个峰值所在位置即可」,所以只需要返回第一个较大值即可
-
解法2:二分查找 本题二分查找解法与上题二分查找解法一致,因为题目提到「返回任何一个峰值所在位置即可」,所以二段性区间可以假设性得分为:1. 左侧小于峰值 2. 右侧小于等于峰值,同样,根据这个二段性区间,可以考虑选用找左侧端点模板
关键步骤:
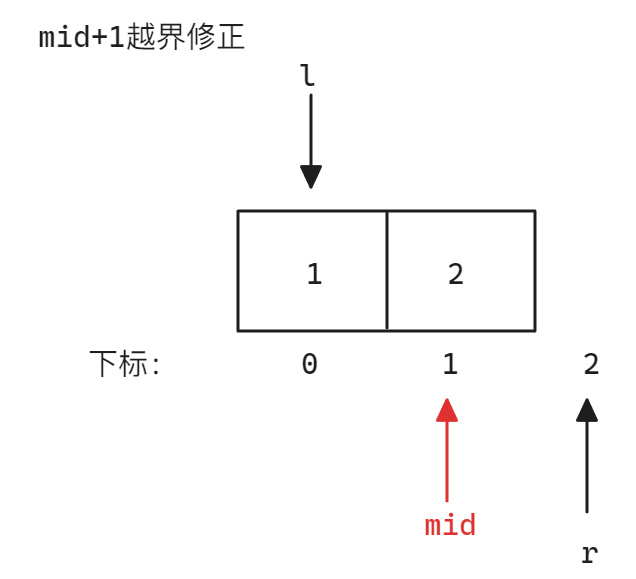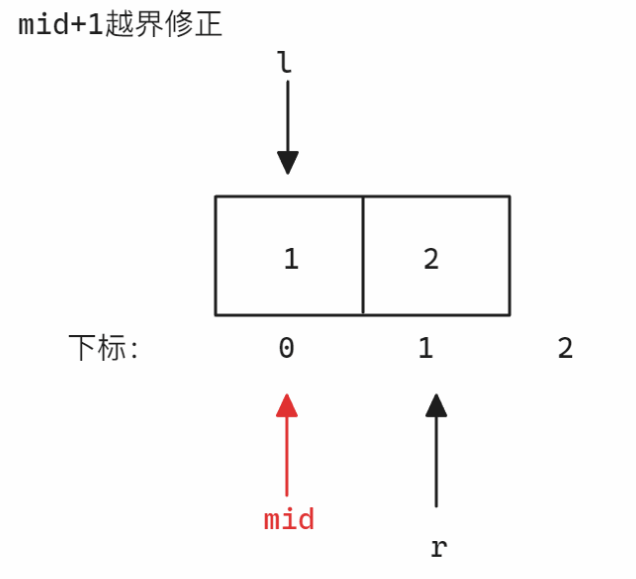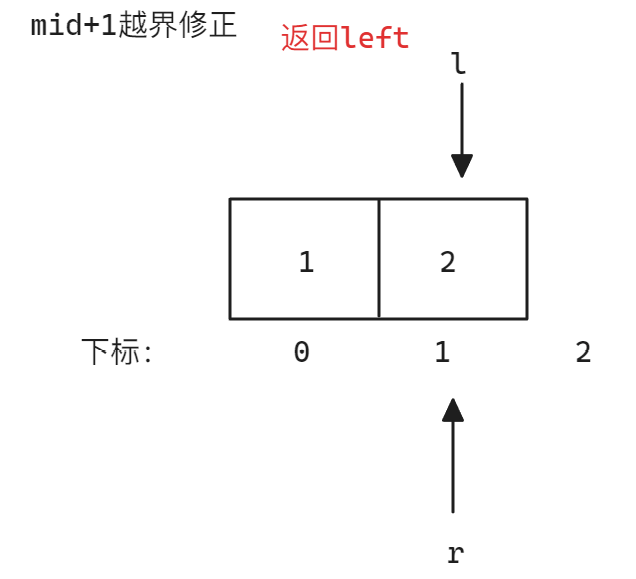
本题需要注意,题目提到了一个关键条件「你可以假设nums[-1]=nums[n]=-∞」,所以如果存在一个数组满足nums[0]>nums[1]或者nums[nums.size()]>nums[nums.size() - 1],则其中的nums[0]和nums[nums.size()]也算是峰值,所以这种情况需要对mid+1进行判断,如果mid+1已经大于nums.size(),就需要修正,修正方法就是通过让right先移动一次再移动left
以[1,2]为例,修正示意图如下:
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | |
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | |
牛客NC107.寻找峰值¶
参考代码:
| C | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | |
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | |
| C | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 | |
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | |
力扣153.寻找旋转排序数组中的最小值¶
问题描述:
Quote
已知一个长度为n的数组,预先按照升序排列,经由1到n次旋转后,得到输入数组。例如,原数组nums = [0,1,2,4,5,6,7]在变化后可能得到:
- 若旋转4次,则可以得到
[4,5,6,7,0,1,2] - 若旋转7次,则可以得到
[0,1,2,4,5,6,7]
注意,数组[a[0], a[1], a[2], ..., a[n-1]]旋转一次 的结果为数组[a[n-1], a[0], a[1], a[2], ..., a[n-2]]。
给你一个元素值互不相同的数组nums,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的最小元素。
你必须设计一个时间复杂度为\(O(\log_{2}{N})\)的算法解决此问题。
示例 1:
| C++ | |
|---|---|
1 2 3 | |
示例 2:
| C++ | |
|---|---|
1 2 3 | |
示例 3:
| C++ | |
|---|---|
1 2 3 | |
思路分析:
-
解法1:暴力解法 本题的暴力解法也很简单,只需要找到最小元素即可
-
解法2:二分查找 本题的查找区间依旧不满足二分查找的前提条件,但是只要能找到二段性,依旧可以使用二分查找算法解决。本题的二段性比较困难,如果根据题目的「最小元素」作为切入点,会发现找出的并非是满足二段性的区间,而是分成了三个区间:1. 左侧(如果存在)大于最小元素 2. 当前最小元素 3. 右侧(如果存在)大于最小元素。以
[3,4,5,1,2]为例,如果以「最小元素」为切入点,则会发现最小元素两侧都大于最小元素,所以无法根据这个切入点划分满足二段性的区间。观察数组,可以发现数组的一个特点:持续递增后,到达某一个最大值之后,从下一个最小值再持续递增,所以可以根据这个特点分为两个满足二段性的区间:1. 第一个持续递增区间 2. 第二个持续递增区间
关键步骤:
有了区间之后开始进行比较,如果当前值大于第二个区间的最大值,则说明第一个区间绝对没有最小值,此时就更新left从而接近第二个区间,否则更新right从而接近第一个区间,这里考虑找左端点,所以依旧使用左端点模板。注意不要使用右端点,因为根据二段性区间,第一个持续递增区间和第二个持续递增区间都是满足严格递增,所以两个区间之中的最小值一定是其中一个区间的第一个元素
Note
本题需要注意与力扣852题、力扣162和牛客NC107作区分,本题涉及到目标值左侧和右侧都比目标值大,所以整个图形呈现向下凹的形状
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | |
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | |
力扣LCR173.点名¶
问题描述:
Quote
某班级n位同学的学号为0 ~ n-1。点名结果记录于升序数组records。假定仅有一位同学缺席,请返回他的学号。
示例 1:
| C++ | |
|---|---|
1 2 | |
示例 2:
| C++ | |
|---|---|
1 2 | |
思路分析:
-
解法1:暴力解法
根据题目描述学生的学号从0开始,一直到
n,所以数组的元素一定最后一个值为n,通过一层for循环依次枚举,直到枚举到与数组中不相等的数值就停止,此时该值就是缺失的值,需要注意,这个方法如果缺失的值是最后一个值n需要额外判断 -
解法2:异或运算
这个解法与第一种解法基本一致,根据异或运算的特点,当出现非0值与0异或会得出原数值,相同的值异或得0,所以根据这个特点可以获取到第一个非0的值即为缺失值
-
解法3:哈希表
题目中的提示内容可以看到数据范围最大到10000,所以可以开辟一个数组用于直接定址,将数组中的数值依次映射到哈希表中,再遍历哈希表找到值为0的即为缺失值
-
解法4:数学(等差数列)
因为题目中提到学号从0开始一直到
n,中间的每一个值间隔为1,所以可以利用等差求和公式先计算出不缺失值时数组的总和,再用总和减去当前缺失数值时的数组的总和,结果就是缺失值 -
解法5:二分查找
本题的二分查找比较隐晦,如果单单看数值可能很难找出关系,可以考虑结合下标看,本题最大的特点就是每一个同学的学号与其下标相同,如果遇到缺失值,则下标就会比对应值小1,根据这个特点,推导出满足二段性的区间:1. 与下标相等 2. 与下标差1
关键步骤:
主要讨论第5种解法,有了满足二段性的区间,只需要找到第一个下标与对应值不等的即为缺失值,当下标与对应值相等,说明当前位置及之前位置均没有缺失值,更新left减小区间,否则更新right以结束循环
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | |
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | |
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | |
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 | |
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | |