跳转至

前缀和

约 7853 个字 710 行代码 15 张图片 预计阅读时间 35 分钟

介绍

在计算数组元素之和时，最直观的思路就是依次遍历数组取出元素并相加，但是这个思路的时间复杂度为\(O(N)\)，如果数组元素非常多，就会面临执行时间长的问题

为了尽可能降低操作时间，考虑一种思路：每一次计算当前元素以及之前的元素之和存储到一个新的数组中，当需要获取原数组指定位置之前的元素之和时，只需要在新数组中的对应位置找到结果即可

例如下面的一个示例：

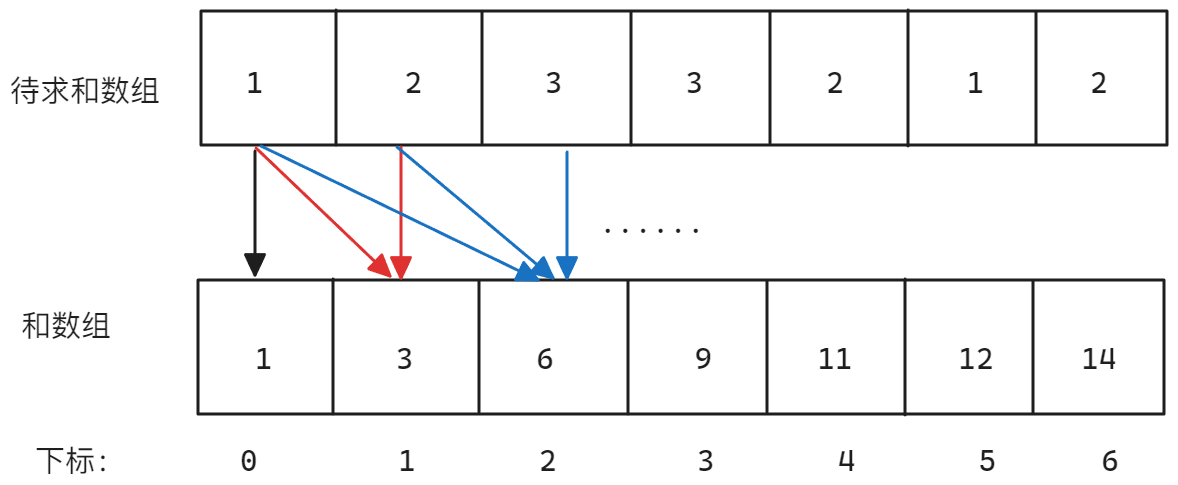
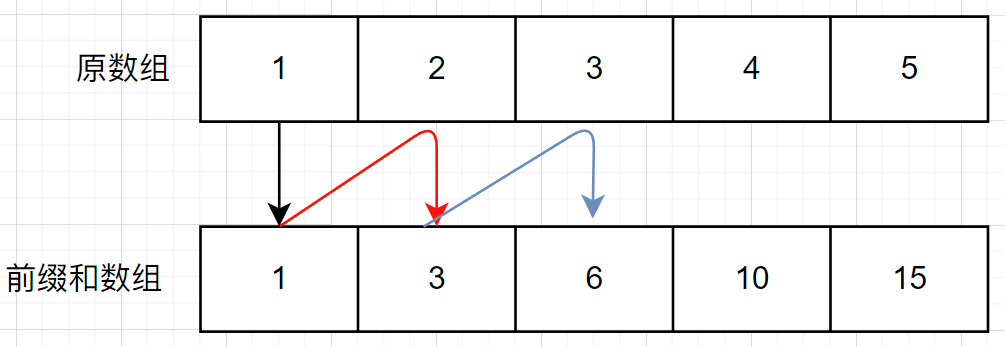
假设要计算一个数组[1,2,3,3,2,1,2]，则其和的数组为[1,3,6,9,11,12,14]，计算过程如下图所示：

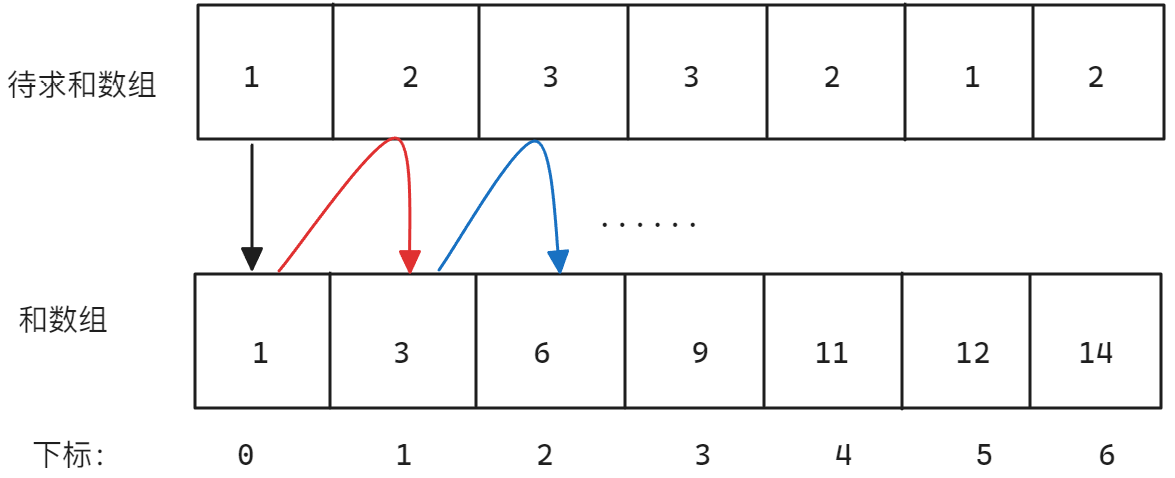
但是观察数组的形式，和数组当前位置的前一个位置就是原数组当前位置之前的元素之和，而需要计算原数组当前位置及之前元素的总和就只需要将当前位置之前的和加上当前元素即可，所以，上面的加法过程还可以简化为如下步骤：

在上图中可以看出，需要求从0号位置开始，到1号位置结束的元素之和就只需要在和数组中直接取出1号位置的元素即可获得两个元素的和。同理，需要求1号位置开始，到5号位置结束，中间的元素之和，只需要让和数组中5号位置的元素减去1号位置之前的元素即可获得原数组从1号位置开始，到5号位置结束的元素之和

假设待求和的数组为arr，和数组为sum，则上面的描述用下面的表达式表示为：

  1. 从0号位置开始，到1号位置结束的元素之和 arr[0] + arr[1] = sum[1]
  2. 从1号位置开始，到5号位置结束，中间的元素之和 arr[1] + arr[2] + arr[3] + arr[4] + arr[5] = sum[5] - sum[0]

在上面的例子中，和数组sum存储的值是当前位置的元素及其前面所有元素的和，所以这个和也被称为「前缀和」，而对应的和数组sum被称为「前缀和数组」。在前面也看到，前缀和最常用的题型就是计算一个连续区间的和

示例题目

卡码网KamaCoder58.区间和

问题描述：

Quote

题目描述

给定一个整数数组Array，请计算该数组在每个指定区间内元素的总和。

输入描述

第一行输入为整数数组 Array 的长度n，接下来n行，每行一个整数，表示数组的元素。随后的输入为需要计算总和的区间下标：a，b （b > = a），直至停止输入（遇到文件末尾）

输出描述

输出每个指定区间内元素的总和。

输入示例

C++
1
2
3
4
5
6
7
8
5
1
2
3
4
5
0 1
1 3

输出示例

C++
1
2
3
9

思路分析：

  1. 解法1：暴力解法

    本题的暴力解法就是前面提到的根据区间划分起始位置和终止位置，从起始位置开始依次向后遍历直到终止位置，在遍历过程中累加获取到的元素即可求出区间和，但是这个解法在数据量巨大时会超时

  2. 解法2：前缀和

    思路见前面的介绍

关键步骤：

本题最关键的问题就是求前缀和以及获取指定区间的和

首先对于求前缀和，考虑下面两种方式：

  1. 假设sum为前缀和数组，arr为原数组，i为下标（从0开始），代码如下：

    C++
    1
    sum[i] += arr[i] + sum[i - 1];

  2. 假设sumArr存储元素之和，sum为前缀和数组，arr为原数组，i为下标（从0开始），代码如下：

    C++
    1
2
    sumArr += arr[i];
sum[i] = sumArr;

这两种方式中，第一种方式是一种当前情况下是不合适的求和方式，因为如果i为第一个元素，则对于第一个元素来说就需要单独进行处理，即sum[i] = arr[i]，而第二种方式适用性更加广泛，所以推荐第二种

接下来考虑获取指定区间的和，从前面的介绍可以看出，如果指定区间的起始位置为0下标，则直接获取终止位置在前缀和数组中对应的值即可，但是对于起始位置不是0下标，则需要通过终止位置在前缀和数组中对应的值减去起始位置的前一个位置的下标在前缀和数组中对应的值，根据题目，a为起始位置，b为终止位置，结果为result，代码表示如下：

C++
1
2
3
4
if(!a)
    result = sum[b];
else
    result = sum[b] - sum[a - 1];

优化思路：

前面提到两种求前缀和的方式，如果前缀和数组下标从0开始，就必须采用第二种方式，并且在使用前缀和数组时还有单独考虑起始位置为0的情况，整个过程中的步骤有点繁琐。现在考虑如何使用第一种方式从而去除繁杂的分支语句，因为当前缀和数组下标为0时，sum[a-1]就会变为sum[-1]，那么就考虑让和数组的有效元素从下标1位置开始存储，同时也让原数组的有效元素从1位置开始存储，否则a依旧可以为0。使用这种做法就可以确保sum[a-1]变为sum[0]而不是sum[-1]

现在就需要考虑第二个问题，sum[0]的值是多少合适，很明显，一个数加0还是原数，一个数减去0也是原数，所以sum[0]=0

根据前面的优化思路，就可以对代码进行优化

首先是开辟原数组和前缀和数组，假设n代表数组中的元素个数，代码如下：

C++
1
2
3
4
// 原数组
vector<int> arr(n + 1);
// 前缀和数组
vector<int> sum(n + 1);

接着是求前缀和存储到前缀和数组中，代码如下：

C++
1
2
// 当前元素+之前元素的和
sum[i] = arr[i] + sum[i - 1];

最后就是使用前缀和数组，根据题目要求可知左边界为a，右边界为b，假设结果为result，代码如下：

C++
1
2
// 当前元素及之前元素的总和减去左边界前一个元素及其之前所有元素的和
result = sum[b] - sum[a - 1];

思考问题：

原数组是否一定需要从下标为1位置开始存储？

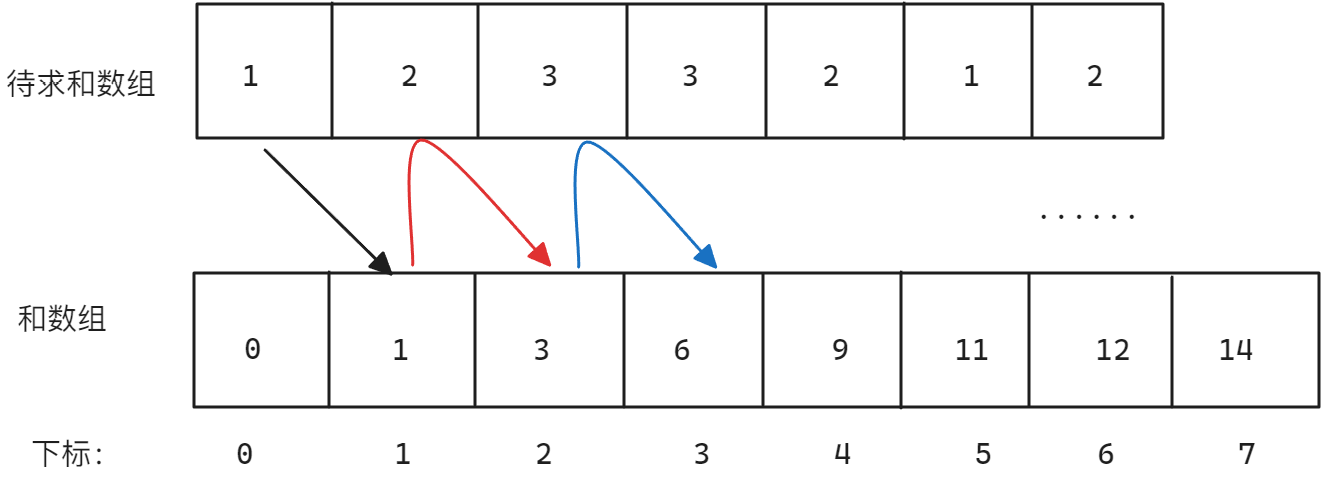
其实可以不需要，但是在计算前缀和时需要正确映射，否则可能越界，示意图如下：

观察上图，可以看到当计算原数组中第一个元素（下标为0）的和时，其和映射在前缀和数组第二个元素的位置（下标为1），计算原数组中第二个元素（下标为1）及之前元素的和时，利用原数组的当前元素（下标为1）与前缀和数组中前一个元素（下标为1）进行求和，其和映射在前缀和数组第三个元素的位置（下标为2）。假设sum代表前缀和数组，arr代表原数组，i代表下标（原数组有效元素从0开始，前缀和数组有效元素从1开始），可以推出求和代码如下：

C++
1
sum[i + 1] = sum[i] + arr[i];

如果不想修改前缀和数组sum的坐标，则代码可以写为

C++
1
2
// i从1开始
sum[i] = sum[i - 1] + arr[i - 1];

Note

注意，sum[0]还是等于0

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <iostream>
#include <vector>
using namespace std;

int main()
{
    // 解除同步
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    // 输入数组长度
    int len = 0;
    cin >> len;

    vector<int> arr(len);

    for(int i = 0; i < len; i++)
        cin >> arr[i];

    int a = 0, b = 0;
    int sum = 0;
    while(cin >> a >> b)
    {
        for(int i = a; i <= b; i++)
            sum += arr[i];
        cout << sum << endl;

        sum = 0;
    }

    return 0;
}
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <iostream>
#include <vector>
using namespace std;

int main()
{
    // 解除同步
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    // 输入数组长度
    int len = 0;
    cin >> len;

    // 元素数组
    // 前缀和数组有效元素从0开始
    vector<int> arr(len);
    // 前缀和数组
    // 前缀和数组有效元素从0开始
    vector<int> sum(len);

    int sumArr = 0;
    for(int i = 0; i < len; i++)
    {
        cin >> arr[i];

        // 计算前缀和
        sumArr += arr[i];
        sum[i] = sumArr;
    }

    int a = 0, b = 0;
    while(cin >> a >> b)
    {
        // 求和
        if(a == 0)
            cout << sum[b] << endl;
        else
            cout << sum[b] - sum[a - 1] << endl;
    }

    return 0;
}
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <iostream>
#include <vector>
using namespace std;

int main()
{
    // 解除同步
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    // 输入数组长度
    int len = 0;
    cin >> len;

    // 元素数组
    // 原数组有效元素从1开始
    vector<int> arr(len + 1);
    // 前缀和数组
    // 前缀和数组有效元素从1开始
    vector<int> sum(len + 1);

    int sumArr = 0;
    for(int i = 1; i <= len; i++)
    {
        cin >> arr[i];
        // i=1时也可以写成
        // cin >> arr[i - 1]

        // 计算前缀和
        sum[i] = sum[i - 1] + arr[i];
        // 也可以写成
        // sum[i] = sum[i - 1] + arr[i - 1];
    }

    int a = 0, b = 0;
    while(cin >> a >> b)
    {
        // 求和
        // 注意本题的a和b都是从0开始
        // 对于长度为len+1的前缀和数组来说，a位置实际上对应的有效元素是sum[a+1]
        // cout << sum[b + 1] - sum[a - 1 + 1] << endl;
        // 简化为
        cout << sum[b + 1] - sum[a] << endl;
    }

    return 0;
}
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <iostream>
#include <vector>
using namespace std;

int main()
{
    // 解除同步
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    // 输入数组长度
    int len = 0;
    cin >> len;

    // 元素数组
    // 原数组有效元素从0开始
    vector<int> arr(len);
    // 前缀和数组
    vector<int> sum(len + 1);

    int sumArr = 0;
    for(int i = 0; i < len; i++)
    {
        cin >> arr[i];

        // 计算前缀和
        sum[i + 1] = sum[i] + arr[i];
    }

    int a = 0, b = 0;
    while(cin >> a >> b)
    {
        // 求和
        cout << sum[b + 1] - sum[a] << endl;
    }

    return 0;
}

模版题目

一维前缀和

牛客网DP34.【模版】前缀和

问题分析：

Quote

描述

给定一个长度为n的数组\(a_1, a_2, ... ,a_n\)

接下来有q次查询, 每次查询有两个参数l, r

对于每个询问, 请输出\(a_l+a_{l+1}+...+a_r\)

输入描述：

第一行包含两个整数n和q

第二行包含n个整数，表示\(a_1, a_2, ...a_n\)

接下来q行，每行包含两个整数l和r

其中，

\(1 \le n, q \le 10^5\)

\(-10^9 \le a[i] \le 10^9\)

\(1 \le l \le r \le n\)

输出描述：

输出q行，每行代表一次查询的结果

思路分析：

  1. 解法1：暴力解法

    与示例题目一致

  2. 解法2：前缀和

    与示例题目一致

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <iostream>
#include <vector>
using namespace std;

int main() 
{
    int n, q;
    while (cin >> n >> q) 
    {
        // 注意使用long long防止溢出
        long long sumArr = 0;
        vector<long long> arr(n);
        vector<long long> sum(n);
        for (int i = 0; i < n; i++) 
        {
            cin >> arr[i];
            sumArr += arr[i];
            sum[i] = sumArr;
        }

        int l = 0, r = 0;
        for (int i = 0; i < q; i++) 
        {
            cin >> l >> r;

            if (l - 1 == 0) 
            {
                cout << sum[r - 1] << endl;
            } 
            else 
            {
                cout << sum[r - 1] - sum[l - 2] << endl;
            }
        }
    }
}
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <iostream>
#include <vector>
using namespace std;

int main() 
{
    int n, q;
    while (cin >> n >> q) 
    {
        // 注意使用long long防止溢出
        vector<long long> arr(n + 1);
        vector<long long> sum(n + 1);
        for (int i = 1; i <= n; i++) 
        {
            cin >> arr[i];
            sum[i] = sum[i - 1] + arr[i];
        }

        int l = 0, r = 0;
        for (int i = 0; i < q; i++) 
        {
            cin >> l >> r;

            cout << sum[r] - sum[l - 1] << endl;
        }
    }
}
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <iostream>
#include <vector>
using namespace std;

int main() 
{
    int n, q;
    while (cin >> n >> q) 
    {
        // 注意使用long long防止溢出
        vector<long long> arr(n);
        vector<long long> sum(n + 1);
        for (int i = 0; i < n; i++) 
        {
            cin >> arr[i];
            sum[i + 1] = sum[i] + arr[i];
        }

        int l = 0, r = 0;
        for (int i = 0; i < q; i++) 
        {
            cin >> l >> r;

            cout << sum[r] - sum[l - 1] << endl;
        }
    }
}

二维前缀和

牛客网DP34.【模版】二维前缀和

问题描述：

Quote

描述

给你一个n行m列的矩阵 A ，下标从1开始。

接下来有q次查询，每次查询输入 4 个参数x1,y1,x2,y2

请输出以(x1, y1)为左上角，(x2,y2)为右下角的子矩阵的和

输入描述：

第一行包含三个整数n,m,q

接下来n行，每行m个整数，代表矩阵的元素

接下来q行，每行4个整数x1,y1,x2,y2，分别代表这次查询的参数

其中，

\(1 \le n, m \le 1000\)

\(1 \le q \le 10^5\)

\(-10^9 \le a[i][j] \le 10^9\)

\(1 \le x_1 \le x_2 \le n\)

\(1 \le y_1 \le y_2 \le m\)

输出描述：

输出q行，每行表示查询结果

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
输入：
3 4 3
1 2 3 4
3 2 1 0
1 5 7 8
1 1 2 2
1 1 3 3
1 2 3 4
输出：
8
25
32

思路分析：

  1. 解法1：暴力解法

    本题的暴力解法就是直接遍历求和

  2. 解法2：前缀和

    本题是二维数组的前缀和，所以需要考虑如何计算二维数组的前缀和。二维数组前缀和的计算方式与一维数组前缀和基本类似，但是二维数组因为需要考虑横向坐标，所以计算每一个二维数组的前缀和数组的值相当于一个范围的面积

关键步骤：

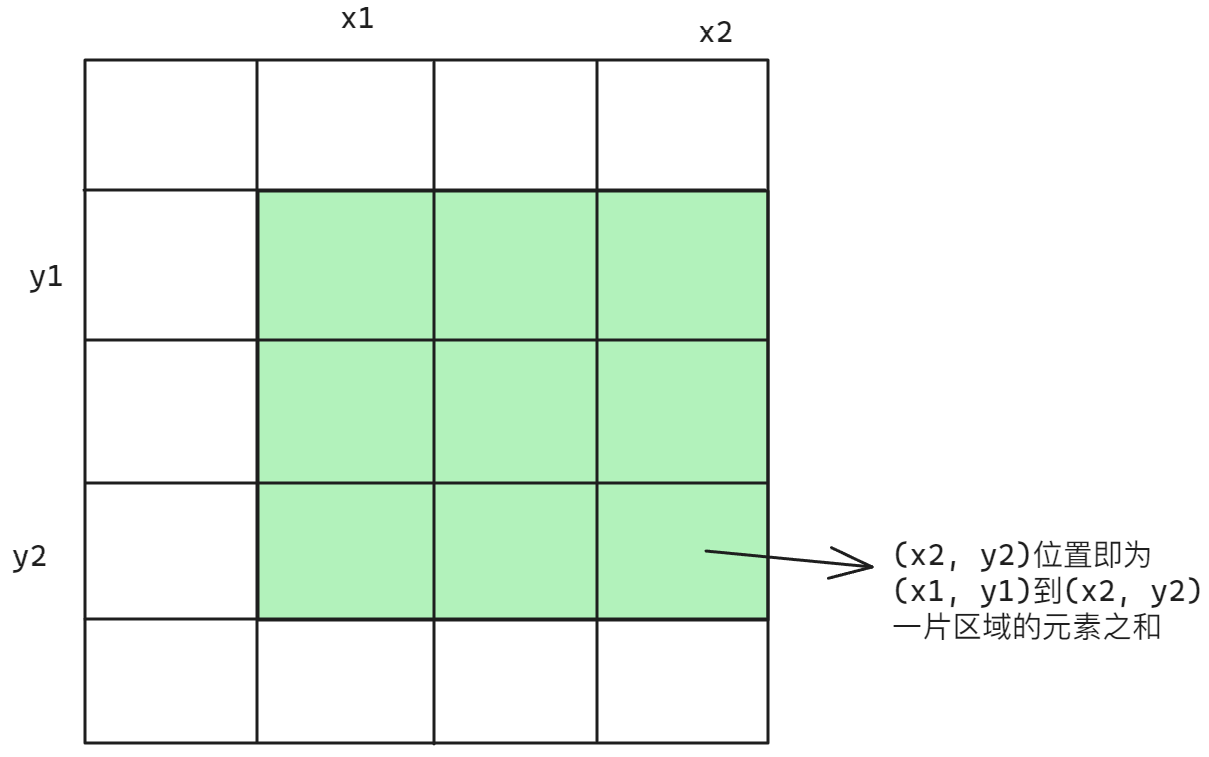
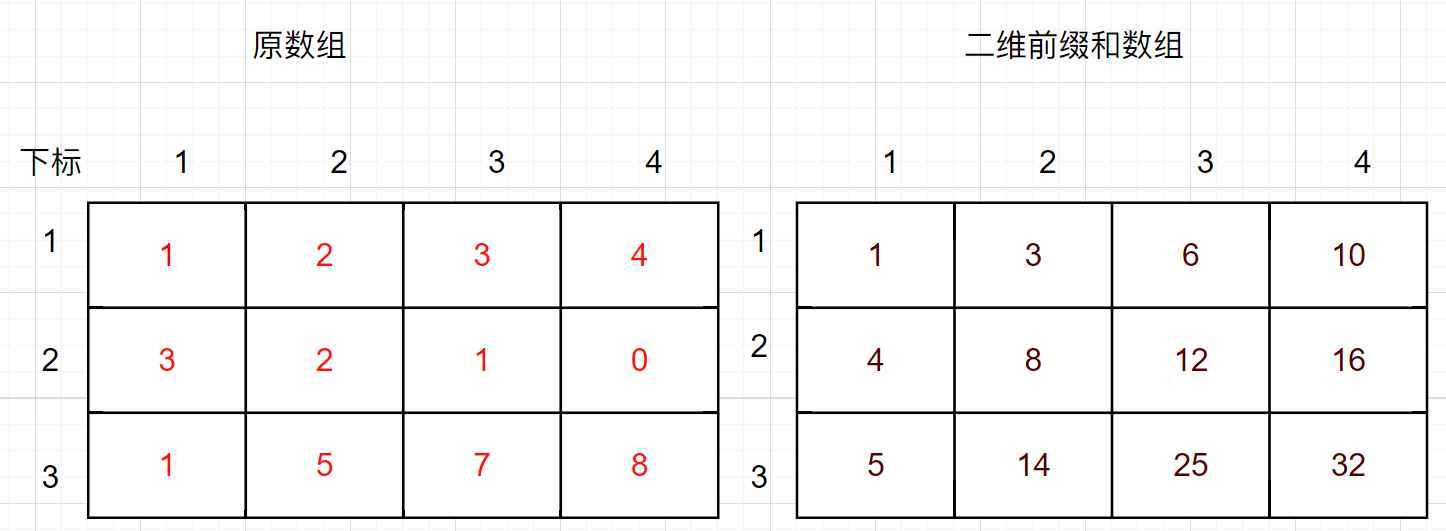
假设二维数组arr的左上角坐标为(x1, y1)，右下角的坐标为(x2, y2)，则在二维前缀和数组中坐标为(x2, y2)的位置即为(x1, y1)和(x2, y2)围成的一片区域对应原数组该区域的所有元素之和，假设原数组和前缀和数组有效元素均从下标1开始，示意图如下：

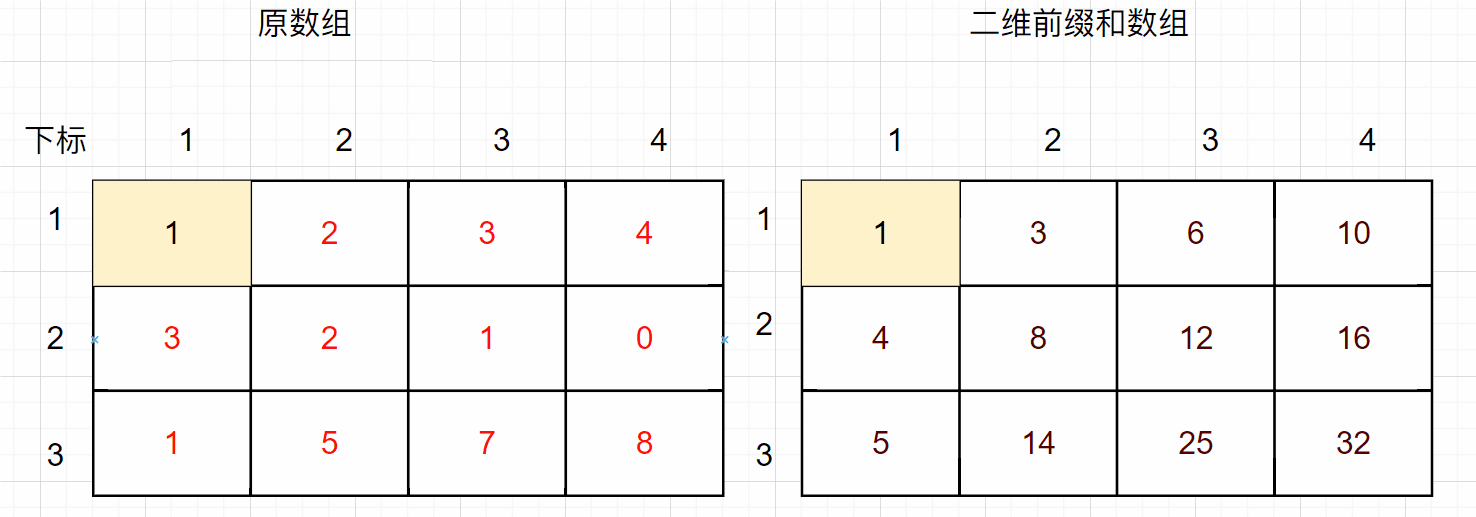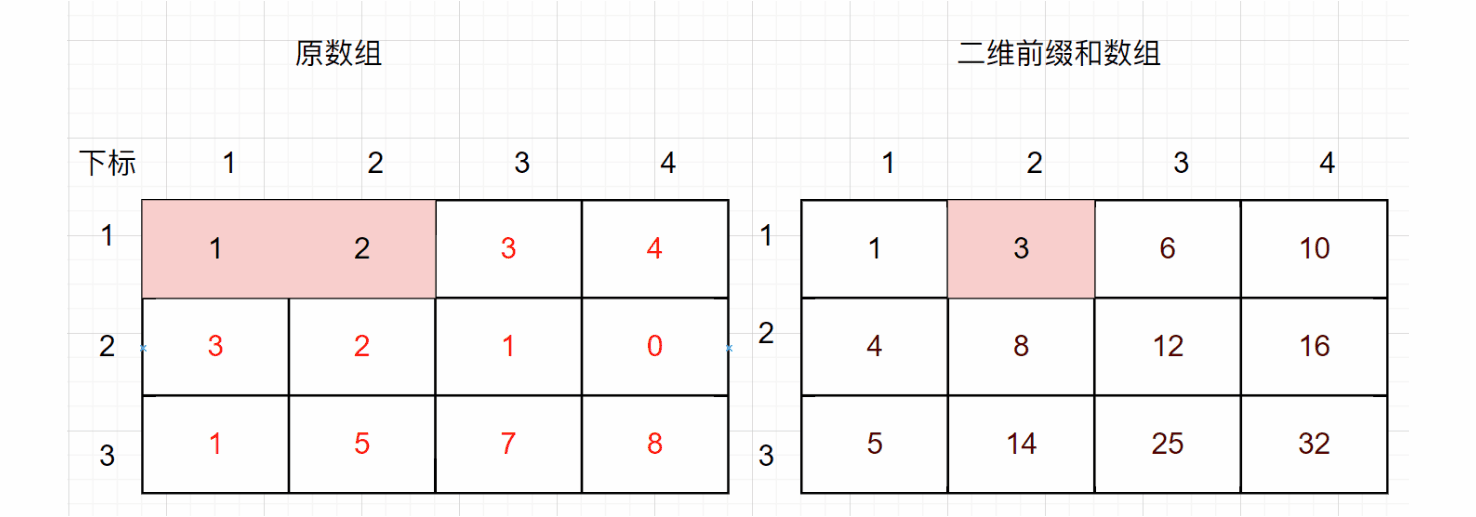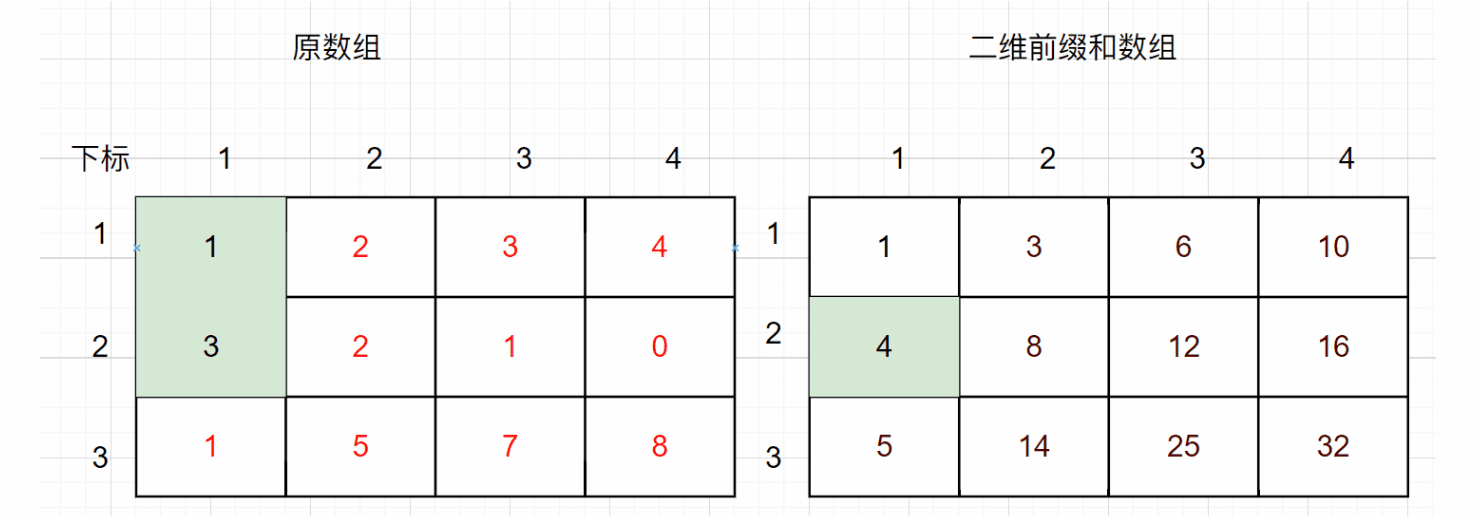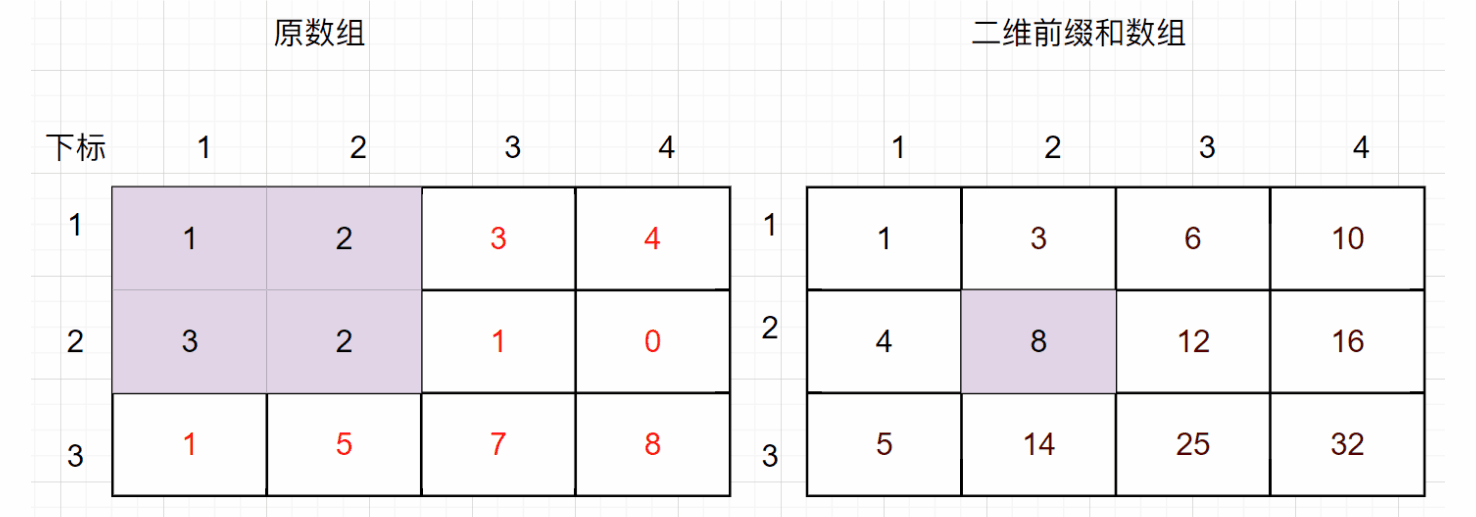
以题目示例为例，给出一个3行4列的数组，数组内容为[[1,2,3,4],[3,2,1,0],[1,5,7,8]]，假设原数组和前缀和数组有效元素均从下标1开始，对应二维前缀和数组中的值为如下，其中给出了部分前缀和数组元素对应的原数组元素之和：

下面给出部分前缀和计算方式的示意图：

理解了如何计算二维前缀和数组，与一维前缀和数组一样，二维数组的前缀和数组也涉及到两个方面：1. 构建二维前缀和数组 2. 使用二维前缀和数组

对于构建二维前缀和数组来说，假设需要计算前缀和数组第i行，第j列的值，计算方式有两种：

  1. 暴力求和

    暴力求和的方式很简单，只需要遍历一遍原二维数组，在遍历过程中处理累加即可，但是这个效率很低，所以不重点考虑

  2. 根据数学规律求和

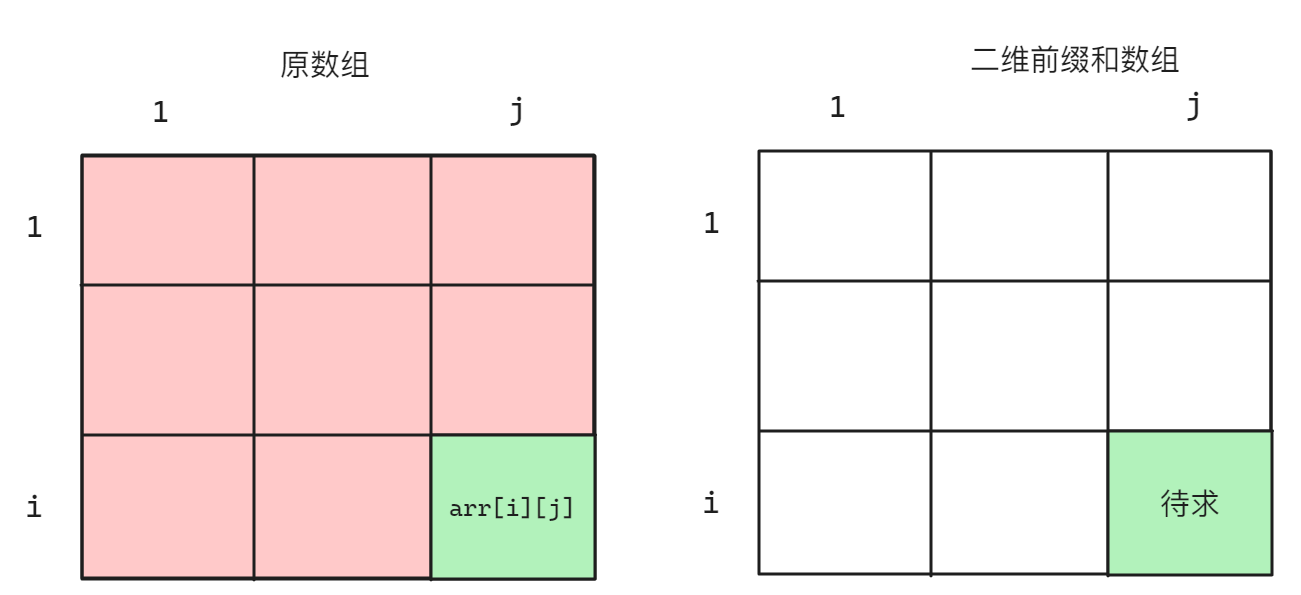
    在二维前缀和数组中，第i行，第j列的数据即为从[1][1]到[i][j]位置所构成的区域中所有元素之和，当前已知原数组第i行第j列的元素为arr[i][j]，而需要计算从[1][1]到[i][j]位置所构成的区域中所有元素之和，只需要将arr[i][j]与前缀和数组sum从sum[1][1]到sum[i][j]位置所构成的区域（不包含sum[i][j]）的元素之和加上arr[i][j]即可

    示意图如下：

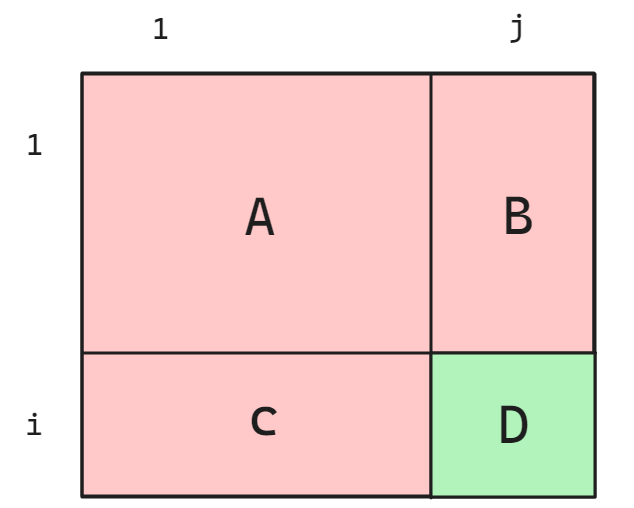
    根据上面的图进行抽象划分可以划分出4个区域，分别表示为A、B、C和D，如下图所示：

    有了抽象图后，将前面的思路转化为sum[i][j] = A+B+C+D

    因为图中B区域和C区域的面积不容易获取，所以考虑先获取A+B区域和A+C区域的元素之和，因为D区域的横坐标为i，纵坐标为j，所以可以得出在二维前缀和数组中A+B区域之和为sum[i-1][j]，同理可以获取到A+C区域元素之和为sum[i][j-1]，计算过程中可以发现，A区域被计算了两次，所以需要再减去一次A区域的元素之和sum[i-1][j-1]

    所以前面的表达式可以转化为：sum[i][j] = A+B+A+C-A+D = sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1] + arr[i][j]。这个表达式也就是求二维前缀和数组每一个元素的通用表达式，但是前提是第一个有效元素的下标为1

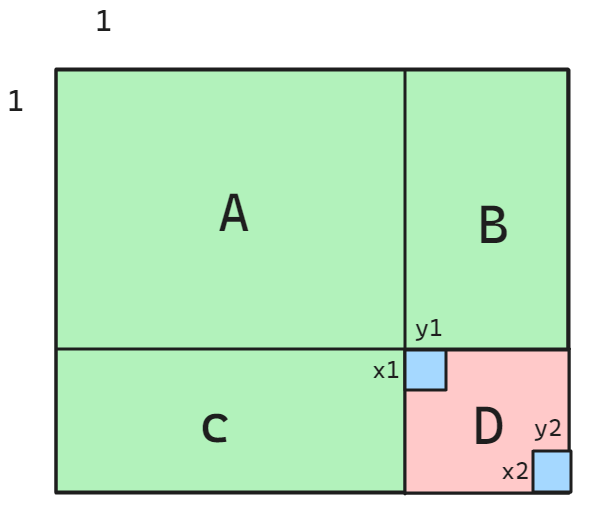
有了二维前缀和数组后，就需要根据具体区间要求使用二维前缀和数组，使用思路与前面构建二维前缀和数组的思路基本一致。根据题目要求，起始位置为(x1, y1)，终止位置为(x2, y2)，同样使用A、B、C和D四个区域，假设D表示待求区域的元素之和，则对问题进行抽象化,如下图所示：

因为D区域表示从arr[1][1]到arr[x2][y2]所围成区域的所有元素之和，所以可以考虑使用总和减去A、B和C区域之和间接获取到D区域的元素之和，所以思路转化为arr[x1][y2]到arr[x2][y2]区域元素之和result=sum[x2][y2] - (A + B) - (A + C) + A，注意因为多减了一次A，所以需要再加上一个A区域

而A+B区域即为sum[x1-1][y2]，A+C区域即为sum[x2][y1-1]，而A区域即为sum[x1-1][y1-1]

所以result化简为sum[x2][y2] - sum[x1-1][y2] - sum[x2][y1-1]+sum[x1-1][y1-1]

思考问题：

  1. 二维前缀和数组的有效元素都是从1开始的，那么如果获取的是sum[0][j]或者sum[i][0]的数据是多少呢？

    与一维前缀和数组一样，在二维前缀和数组中，第0行和第0列的元素均为0

  2. 二维原数组是否一定需要从1号位置开始计数呢？

    其实并不是，与一维前缀和一样，可以满足原数组有效数据从下标0位置开始，而前缀和数组从1位置开始在，只需要将原数组存储位置改变即可，其他不变，包括构建前缀和数组公式和使用前缀和公式

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <iostream>
#include <vector>
using namespace std;

int main() 
{
    int n = 0, m = 0;
    int q = 0;
    while(cin >> n >> m >> q)
    {
        // 原数组
        vector<vector<long long>> arr(n + 1);
        for(auto& v : arr)
        {
            v.resize(m + 1);
        }
        // 和数组
        vector<vector<long long>> sum(n + 1);
        for(auto& v : sum)
        {
            v.resize(m + 1);
        }

        // 读取数组并填充前缀和
        for(int i = 1; i <= n; i++)
        {
            for(int j = 1; j <= m; j++)
            {
                cin >> arr[i][j];

                // 填充前缀和数组
                sum[i][j] = sum[i - 1][j] + sum[i][j - 1] + arr[i][j] - sum[i - 1][j - 1];
            }
        }

        int x1 = 0, x2 = 0, y1 = 0, y2 = 0;
        // 使用前缀和数组
        for(int i = 0; i < q; i++)
        {
            cin >> x1 >> y1 >> x2 >> y2;
            cout << sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1] << endl;
        }
    }
}
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <iostream>
#include <vector>
using namespace std;

int main() 
{
    int n = 0, m = 0;
    int q = 0;
    while(cin >> n >> m >> q)
    {
        // 原数组，从 arr[0][0] 开始
        vector<vector<long long>> arr(n, vector<long long>(m));
        // 和数组，仍从 sum[1][1] 开始
        vector<vector<long long>> sum(n + 1, vector<long long>(m + 1, 0));

        // 读取数组并填充前缀和
        for(int i = 1; i <= n; i++)
        {
            for(int j = 1; j <= m; j++)
            {
                cin >> arr[i-1][j-1];

                // 填充前缀和数组
                sum[i][j] = sum[i - 1][j] + sum[i][j - 1] + arr[i-1][j-1] - sum[i - 1][j - 1];
            }
        }

        int x1 = 0, x2 = 0, y1 = 0, y2 = 0;
        // 使用前缀和数组
        for(int i = 0; i < q; i++)
        {
            cin >> x1 >> y1 >> x2 >> y2;
            cout << sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1] << endl;
        }
    }
}

一维前缀和与二维前缀和公式

一维前缀和：

假设原数组有效元素从0位置开始，则有：

构建前缀和数组公式：

C++
1
sum[i] = sum[i - 1] + arr[i - 1];

假设结果存储到result中，使用前缀和数组公式：

C++
1
result = sum[b] - sum[a - 1];

二维前缀和：

假设原数组有效元素从0位置开始，则有：

构建前缀和数组公式：

C++
1
sum[i][j] = sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1] + arr[i-1][j-1];

假设结果存储到result中，使用前缀和数组公式：

C++
1
result = sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1];

相关题目

卡码网kamaCoder44.开发商购买土地

卡码网kamaCoder44.开发商购买土地

问题描述：

Quote

题目描述

在一个城市区域内，被划分成了n * m个连续的区块，每个区块都拥有不同的权值，代表着其土地价值。目前，有两家开发公司，A公司和B公司，希望购买这个城市区域的土地。

现在，需要将这个城市区域的所有区块分配给A公司和B公司。

然而，由于城市规划的限制，只允许将区域按横向或纵向划分成两个子区域，而且每个子区域都必须包含一个或多个区块。为了确保公平竞争，你需要找到一种分配方式，使得A公司和B公司各自的子区域内的土地总价值之差最小。

注意：区块不可再分。

输入描述

第一行输入两个正整数，代表n和m

接下来的n行，每行输出m个正整数

输出描述

请输出一个整数，代表两个子区域内土地总价值之间的最小差距

输入示例

C++
1
2
3
4
3 3
1 2 3
2 1 3
1 2 3

输出示例

C++
1
0

提示信息

如果将区域按照如下方式划分：

C++
1
2
3
1 2 | 3
2 1 | 3
1 2 | 3

两个子区域内土地总价值之间的最小差距可以达到0

数据范围

1 <= n, m <= 100

n和m不同时为1

思路分析：

根据题意，本题要求两个公司各自可以分得的土地总价值，并且进行两种方向的划分，而所谓总价值就是指定区域的数组元素之和，所以可以考虑使用前缀和。因为本题提到「只允许将区域按横向或纵向划分成两个子区域」，所以就可以不用考虑使用二维前缀和，尽管题目说到是一个「n * m个连续的区块」，所以本题可以考虑先进行横向划分计算出一个较小值，再进行纵向划分计算出一个值与之前的横向划分比较取一个最小值即为结果

关键步骤：

本题并不真的需要构建一个前缀和数组，只需要依次求和先算出当前矩阵所有的元素之和，在横向划分中，先给某一方分一片土地，根据总和减去分给该方的土地就可以得出另一方所获得的土地，取出二者元素之和的最小差值即可，同样的思路应用于纵向划分，最后求出较小差值

需要注意的是，在给一方划土地时，因为题目提到「每个子区域都必须包含一个或多个区块」，也就是说A或者B都至少要获得一个区块，所以在横向划分或者纵向划分中都必须保证至少二者当前所有的区域元素之和不为0

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#include <iostream>
#include <vector>
#include <algorithm>
#include <climits>
using namespace std;

int main()
{
    int n = 0, m = 0;
    while (cin >> n >> m)
    {
        vector<vector<int>> arr(n, vector<int>(m, 0));
        for (int i = 0; i < n; i++)
        {
            for (int j = 0; j < m; j++)
            {
                cin >> arr[i][j];
            }
        }

        int minNum = INT_MAX;
        // 统计总和
        int sum = 0;
        for (int i = 0; i < n; i++)
        {
            for (int j = 0; j < m; j++)
            {
                sum += arr[i][j];
            }
        }

        // 横向划分
        // 注意保证至少有一方有一块区域
        for (int i = 0; i < n - 1; i++)
        {
            int sumA = 0;
            // 给A划分区域
            for (int x = 0; x <= i; x++)
            {
                for (int y = 0; y < m; y++)
                {
                    sumA += arr[x][y];
                }
            }

            int sumB = sum - sumA;
            minNum = min(minNum, abs(sumA - sumB));
        }

        // 纵向划分
        for (int j = 0; j < m - 1; j++)
        {
            int sumA = 0;
            // 给A划分区域
            for (int x = 0; x < n; x++)
            {
                for (int y = 0; y <= j; y++)
                {
                    sumA += arr[x][y];
                }
            }

            int sumB = sum - sumA;
            minNum = min(minNum, abs(sumA - sumB));
        }

        cout << minNum << endl;
    }

    return 0;
}

力扣724.寻找数组的中心下标

力扣724.寻找数组的中心下标

问题描述：

Quote

给你一个整数数组 nums ，请计算数组的 中心下标 。

数组 中心下标 是数组的一个下标，其左侧所有元素相加的和等于右侧所有元素相加的和。

如果中心下标位于数组最左端，那么左侧数之和视为 0 ，因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。

如果数组有多个中心下标，应该返回 最靠近左边 的那一个。如果数组不存在中心下标，返回 -1 。

示例 1：

C++
1
2
3
4
5
6
输入：nums = [1, 7, 3, 6, 5, 6]
输出：3
解释：
中心下标是 3 。
左侧数之和 sum = nums[0] + nums[1] + nums[2] = 1 + 7 + 3 = 11 ，
右侧数之和 sum = nums[4] + nums[5] = 5 + 6 = 11 ，二者相等。

示例 2：

C++
1
2
3
4
输入：nums = [1, 2, 3]
输出：-1
解释：
数组中不存在满足此条件的中心下标。

示例 3：

C++
1
2
3
4
5
6
输入：nums = [2, 1, -1]
输出：0
解释：
中心下标是 0 。
左侧数之和 sum = 0 ，（下标 0 左侧不存在元素），
右侧数之和 sum = nums[1] + nums[2] = 1 + -1 = 0 。

思路分析：

  1. 解法1：暴力解法

    本题的暴力解法很简单，使用两层for循环，第一层循环控制起始位置，第二层计算其左侧元素之和以及右侧元素之和，分别比较二者是否相等即可找出中心元素，但是这种方法的时间复杂度为\(O(N^2)\)

  2. 解法2：一维前缀和

    本题的第二种方法就是利用一维前缀和数组，因为要满足中心元素的左侧元素之和以及右侧元素之和相等，可以考虑遍历前缀和数组，使用前缀和数组的最后一个元素依次减去当前前缀和数组的元素，直到其满足左侧元素之和以及右侧元素之和相等时，对应的下标就是原数组的中心下标

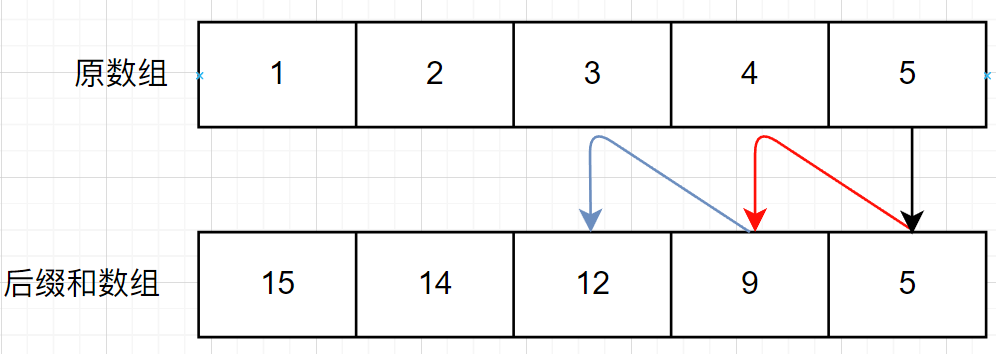
  3. 解法3：前缀和与后缀和

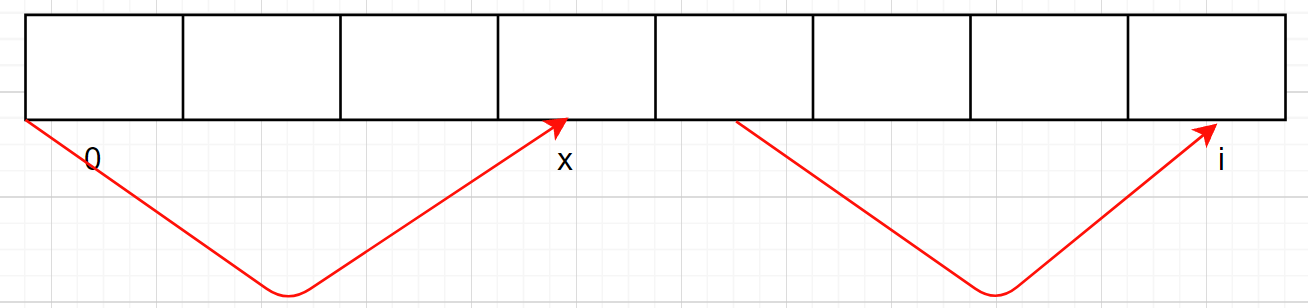
    本题的第三种方法是利用两个和数组，一个表示数组从左向右依次遍历时当前位置及之前的元素之和，另一个数组从右向左依次遍历时当前位置及之前的元素之和，两个数组的作用示意图如下：

    通过两个和数组依次遍历，找到二者相等时元素下标就是整个数组的中心下标

关键步骤：

下面针对后两种解法进行详细讨论；

  1. 解法1：一维前缀和

    直接使用前缀和数组的思路是利用了前缀和数组是存储元素之和的性质，在前缀和数组中，第i个位置的值即为当前及之前所有元素之和，而要判断是否是中心下标元素，就只需要判断当前位置之前的元素之和是否等于其之后的元素之和，所以考虑在遍历前缀和数组的过程中，用数组元素总和减去当前元素及之前的元素之和就可以获取到当前位置及之后的元素之和，而整个过程中只需要判断在前缀和数组中第i-1个位置的元素与元素总和和当前位置元素之差是否相等，从而判断当前i位置是否是中心下标所在位置。

    假设前缀和数组sum从1开始，size表示前缀和数组的长度，根据前面描述可以得出判断是否是中心下标的条件为：sum[size - 1] - sum[i] == sum[i - 1]，如果该条件成立，则i为原数组的中心下标，否则继续遍历前缀和数组直到i到数组结尾。如果i到了前缀和数组结尾也没有遇到中心下标，按照题目要求返回-1即可

  2. 解法2：前缀和与后缀和

    在思路解析部分已经介绍了何为前缀和与何为后缀和，现在就考虑如何利用二者获取到数组的中心下标。数组的中心下标最大的性质就是其之前的元素之和等于其之后的元素之和，但是不论是左侧元素之和还是右侧元素之和，都不包括当前中心下标对应的元素，但是前缀和表示当前位置及其左侧元素之和，后缀和表示当前位置及其右侧元素之和，二者都是计算的和都是包括当前元素，所以在前缀和数组和后缀和数组中可以考虑不加上当前位置的值

    有了上面的思路，接下来根据思路推导出计算公式：

    对于前缀和数组prefix，其有效元素下标从0开始，假设原数组当前位置是i，所以用区间表示法就是[0, i - 1]，其中需要注意的是，当i表示原数组的第一个元素（其下标为0）时，区间变为[0, -1]，是一个不存在的区间，所以需要在遍历原数组之前先将前缀和数组的第一个元素置为0，再从1开始遍历。得出前缀和数组公式为prefix[i] = prefix[i - 1] + nums[i - 1]，其中prefix[i]表示前缀和数组当前位置的元素，prefix[i - 1]表示前缀和数组当前位置之前的元素，nums[i - 1]表示原数组当前位置之前的元素

    同样对于后缀和数组suffix，其有效元素下标从0开始，但是因为后缀和是从后向前遍历，所以第一个被填充的元素是后缀和数组中的最后一个元素，同样，因为不考虑当前元素，假设当前位置为i，则原数组的起始位置应为i+1，而最大值即为原数组的最后一个元素的位置，假设原数组的大小为size，则最后一个元素的位置为size-1，所以有效区间用区间表示法为[i + 1, size - 1]，同样需要注意，当i为size - 1时，区间变为[size, size - 1]也是一个不存在的区间，所以在遍历原数组之前先将后缀和数组的最后一个元素置为0，再从size - 2的位置开始遍历。得出后缀和数组的公式为suffix[i] = suffix[i + 1] + nums[i + 1]，其中suffix[i]表示后缀和数组当前位置的元素，suffix[i + 1]表示后缀和数组当前位置之后的元素，nums[i + 1]表示原数组当前位置之后的元素

    最后，因为前缀和数组和后缀和数组的规模一致，所以只需要一层for循环枚举下标，找到suffix[i] == prefix[i]时的i就是原数组的中心下标

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution724_1
{
public:
    int pivotIndex(vector<int> &nums)
    {
        vector<int> sum(nums.size() + 1);
        // 求出前缀和数组
        for (int i = 1; i <= nums.size(); i++)
        {
            sum[i] = nums[i - 1] + sum[i - 1];
        }

        // 使用前缀和数组
        int index = 0;
        int back = sum[sum.size() - 1];
        for (int i = 1; i < sum.size(); i++)
        {
            if (back - sum[i] == sum[i - 1])
            {
                index = i;
                break;
            }
        }

        return index - 1 == nums.size() ? -1 : index - 1;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution724_2
{
public:
    int pivotIndex(vector<int> &nums)
    {
        vector<int> prefix(nums.size());
        vector<int> suffix(nums.size());

        // 构建前缀和
        // 因为只需要考虑[0, i - 1]区间中的值，所以第i位的值可以不用考虑
        // 当前情况下，前缀和数组的一个元素为0
        // 因为当i=0时，区间为[0, -1]，是一个不存在的区间
        for (int i = 1; i < nums.size(); i++)
            prefix[i] = nums[i - 1] + prefix[i - 1];
        // 构建后缀和
        // 因为只需要考虑[i + 1, size - 1]区间中的值，所以第i位的值可以不用考虑
        // 为了形成错位，需要将suffix[size-1]置为0
        for (int i = nums.size() - 2; i >= 0; i--)
            suffix[i] = nums[i + 1] + suffix[i + 1];

        // 使用前缀和与后缀和
        for (int i = 0; i < nums.size(); i++)
        {
            if (suffix[i] == prefix[i])
            {
                return i;
            }
        }

        return -1;
    }
};

力扣238.除自身以外数组的乘积

力扣238.除自身以外数组的乘积

问题描述：

Quote

给你一个整数数组nums，返回数组answer，其中answer[i]等于nums中除nums[i]之外其余各元素的乘积 。

题目数据 保证 数组nums之中任意元素的全部前缀元素和后缀的乘积都在32位整数范围内。

请不要使用除法，且在O(n)时间复杂度内完成此题。

示例 1:

C++
1
2
输入: nums = [1,2,3,4]
输出: [24,12,8,6]

示例 2:

C++
1
2
输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]

思路分析：

  1. 解法1：暴力解法

    本题的暴力解法就是直接当前位置之前的元素以及其之后的元素相乘即可

  2. 解法2：前缀积和后缀积

    因为不考虑当前元素在内，所以可以通过两个积数组，除了最后处理结果为当前前缀积数组元素和后缀积元素相乘外，其余思路与上一题思路一致

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution238
{
public:
    vector<int> productExceptSelf(vector<int> &nums)
    {
        // 处理结果
        vector<int> ret;

        // 前缀积数组
        vector<int> prefix(nums.size(), 1);
        // 后缀积数组
        vector<int> suffix(nums.size(), 1);

        // 构建前缀积数组
        for (int i = 1; i < nums.size(); i++)
            prefix[i] = prefix[i - 1] * nums[i - 1];

        // 构建后缀积数组
        for (int i = nums.size() - 2; i >= 0; i--)
            suffix[i] = suffix[i + 1] * nums[i + 1];

        // 使用前缀积和后缀积
        for (int i = 0; i < nums.size(); i++)
            ret.push_back(prefix[i] * suffix[i]);

        return ret;
    }
};

力扣560.和为k的子数组

力扣560.和为k的子数组

问题描述：

Quote

给你一个整数数组nums和一个整数k，请你统计并返回该数组中和为k的子数组的个数。

子数组是数组中元素的连续非空序列。

示例 1：

C++
1
2
输入：nums = [1,1,1], k = 2
输出：2

示例 2：

C++
1
2
输入：nums = [1,2,3], k = 3
输出：2

思路分析：

  1. 解法1：暴力解法

    因为是子数组系列的题目，所以暴力解法都是固定一个起始位置和一个终止位置，找到满足条件的区间就记录，否则就不记录，最后返回结果即可

  2. 解法2：前缀和

    本题使用前缀和思路是一种对暴力解法的一种优化，所以先考虑暴力解法的缺陷：多次遍历求和比较，时间复杂度高，为了解决这个问题，就可以考虑使用前缀和先计算出数组元素之和。

关键步骤：

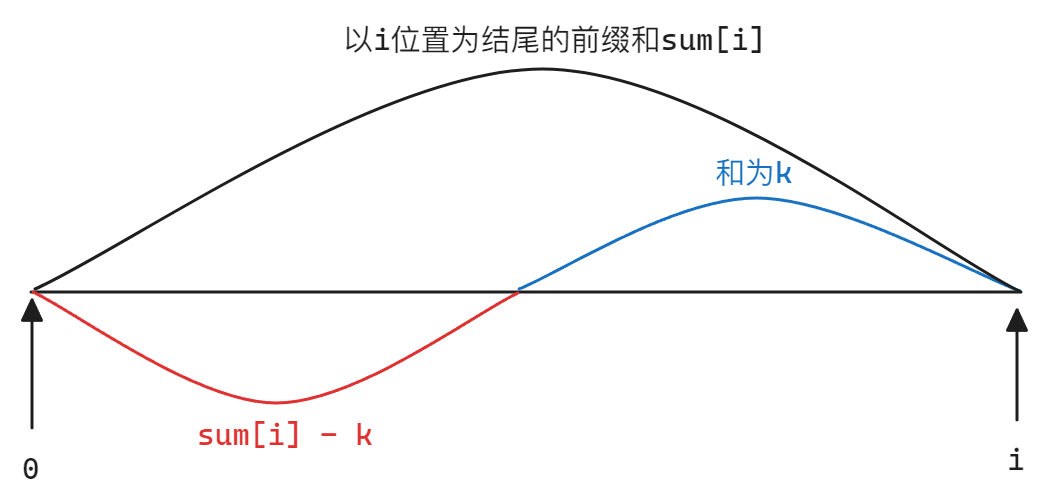
要找到和为k的子数组就需要找到一个指定的区间，但是该区间的起始位置无法确定，如果直接遍历前缀和数组，则还是需要固定一个起始位置和一个终止位置导致时间复杂度退化，此时就可考虑使用正难则反的策略。前面提到前缀和表示当前位置及其之前的元素之和，假设前缀和数组为sum，当前位置为i，那么如果当前位置及其之前元素之和如果存在和为k的区间，则一定就存在sum[i]-k区间，此时就只需要固定终止位置而不需要固定起始位置间接获取到和为k的子数组，也把当前情况下的和为k的子数组称为「以i为结尾和k的子数组」。有了前面的思路，因为sum[i] - k的数量与k的数量是1:1的关系，所以本题就可以转化为「找到一个区间使其和为sum[i] - k」

所谓sum[i] - k就是当前位置去除和为k的部分剩余的连续区间的和，利用一个抽象图表示为如下：

而要求和为sum[i] - k的区间就只需要固定一个起始位置和一个终止位置，使二者构成的区间和为sum[i] - k即可，但是这种做法会使前面的思路前功尽弃，所以考虑另外一种思路，如果将当前区间和看做是tempSum，那么要找和为sum[i] - k的区间，本质就是要找满足tempSum == sum[i] - k的区间，既然涉及到了比较，那么就可以考虑使用一个哈希表进行比较映射，哈希表中存储的就是每一次计算出的前缀和。每一次计算出一个tempSum，就让其进入哈希表，一旦出现一次tempSum == sum[i] - k就说明找到了和为sum[i] - k的区间，此时就只需要更新计数器即可。有了哈希表之后，就只需要考虑计算当前位置及之前的和，也就是当前位置的前缀和即可，而不再需要考虑在计算完所有前缀和完后再通过循环控制区间进行比较，从而保证了时间复杂度

注意问题：

  1. 使用哈希表映射时，在tempSum添加到哈希表和比较tempSum == sum[i] - k两个步骤之间，一定要先进行比较，而不是先添加，因为要保证sum[i] - k和k两个区间的数量关系是1:1，所以在求sum[i] - k时，至少要保证k所在的区间至少有一个元素，所以实际上在求sum[i] - k所在的区间时i的范围为[0, i - 1]。如果先让tempSum添加到哈希表，此时就会出现哈希表本来之前没有出现过sum[i] - k的前缀和，但是因为tempSum先进入了哈希表，导致tempSum == sum[i] - k成立从而更新了计数器。最典型的例子就是原数组为nums = [1], k = 0，如果先添加tempSum，就会导致sum[i] - k值为1，但是这个值原先并不存在，先添加到哈希表并更新计数器就会错误得得到结果为1

  2. 如果整个数组的和为k，此时就会出现sum[i] - k值为0，但是哈希表存储的实际上是当前[0, i - 1]位置的前缀和，所以如果整个数组和为k，则说明[0, i - 1]区间中的所有值的和都是k，此时就意味着sum[i] - k的区间就是[0, i - 1]以外的区间，即一个不存在的区间，所以为了避免这种特殊情况，先在哈希表中存储前缀和为0计数器为1的映射关系

思考问题：

  1. 本题是否可以使用滑动窗口来解决？

    实际上并不可以，因为本题不存在单调性（数据存在负数和0），无法确保一个指向起始位置的指针根据单调性进行移动，而滑动窗口必须要满足单调性才可以使用，所以不能使用滑动窗口

  2. 本题是否一定要创建一个前缀和数组

    实际上并不用，因为有了哈希表的优化，所以就不需要遍历前缀和数组进行比较，而计算前缀和本质就是累加数组的元素，所以只需要一个变量来记录当前位置以及之前的元素之和即可

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution560
{
public:
    int subarraySum(vector<int> &nums, int k)
    {
        // 统计个数
        unordered_map<int, int> cnt;
        // 如果整个数组的元素和为k，则也必须算一次
        cnt[0] = 1;

        int sum = 0;
        int ret = 0;
        for (auto num: nums)
        {
            // 求前缀和
            sum += num;
            // 判断当前前缀和是否等于sum - k
            // 如果等于sum-k代表当前区间内一定存在一个和为k的子数组
            if (cnt.find(sum - k) != cnt.end())
            {
                ret += cnt[sum - k];
            }
            // 记录当前前缀和出现的次数
            cnt[sum]++;
        }

        return ret;
    }
};

力扣974.和可被K整除的子数组

力扣974.和可被K整除的子数组

Note

本题也是蓝桥杯的一道真题：k倍区间

问题分析：

Quote

给定一个整数数组nums和一个整数k，返回其中元素之和可被k整除的非空 子数组 的数目。

子数组是数组中连续`的部分。

示例 1：

C++
1
2
3
4
5
输入：nums = [4,5,0,-2,-3,1], k = 5
输出：7
解释：
有 7 个子数组满足其元素之和可被 k = 5 整除：
[4, 5, 0, -2, -3, 1], [5], [5, 0], [5, 0, -2, -3], [0], [0, -2, -3], [-2, -3]

示例 2:

C++
1
2
输入: nums = [5], k = 9
输出: 0

思路分析：

  1. 解法1：暴力解法

    因为是子数组系列的题目，所以暴力解法都是固定一个起始位置和一个终止位置，找到满足条件的区间就记录，否则就不记录，最后返回结果即可

  2. 解法2：前缀和

    本题可以考虑使用同余定理将题目转化为求一个前缀和满足sum % k == tempSum % k，使用一个哈希表存储余数。剩余的思路与上题思路一致

关键步骤：

需要注意，在C++中，%对应的运算是取余运算，在计算负数对一个正数取余数时会得到一个负数，此时需要进行取余运算修正。与上题一样，如果存在前缀和为0，而0可以整除任何数，所以需要将前缀和0与对应的次数1建立映射关系，并且也不需要真正创建一个前缀和数组

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution974
{
public:
    int subarraysDivByK(vector<int> &nums, int k)
    {
        // 统计前缀和出现的次数
        unordered_map<int, int> cnt;
        cnt[0] = 1;

        int sum = 0;
        int ret = 0;
        for (auto num: nums)
        {
            // 指定区间的前缀和
            sum += num;
            // 取余运算修正
            int rest = (sum % k + k) % k;
            // 如果当前rest存在于哈希表，说明满足sum%k等于之前的余数beforeSum % k
            if (cnt.find(rest) != cnt.end())
            {
                ret += cnt[rest];
            }

            cnt[rest]++;
        }

        return ret;
    }
};

力扣525.连续数组

力扣525.连续数组

问题描述：

Quote

给定一个二进制数组nums, 找到含有相同数量的0和1的最长连续子数组，并返回该子数组的长度。

示例 1:

C++
1
2
3
输入: nums = [0,1]
输出: 2
说明: [0, 1] 是具有相同数量 0 和 1 的最长连续子数组。

示例 2:

C++
1
2
3
输入: nums = [0,1,0]
输出: 2
说明: [0, 1] (或[1, 0]) 是具有相同数量0和1的最长连续子数组。

思路分析：

本题如果直接想使用前缀和会比较难想出思路，但是可以考虑将0看做-1，而要找到数量相等的0和1的最长子数组，就是找到和为0的最长子数组，此时就可以将本题化为「和为k的子数组」，利用「和为k的子数组」的思路即可，但是注意，本次的哈希表的映射关系不再是前缀和与次数，而是前缀和与下标

关键步骤：

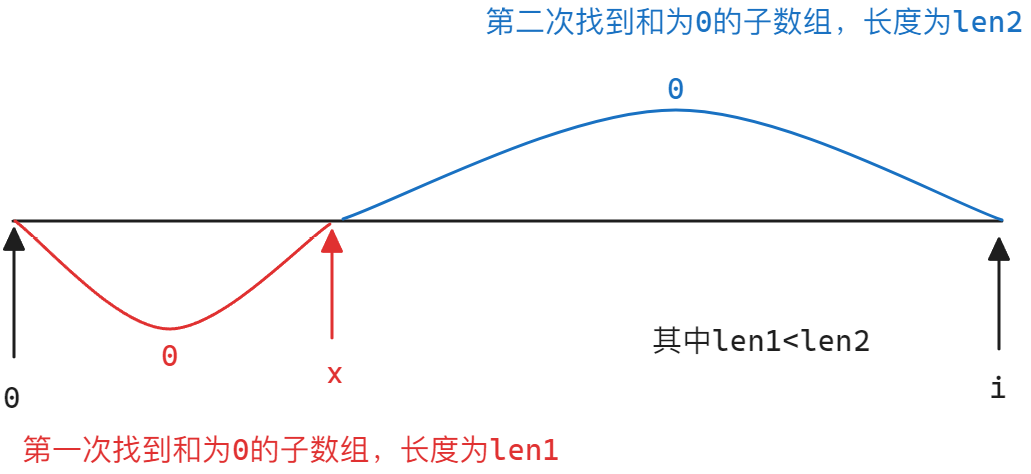
因为要做前缀和与下标的映射，所以需要确定何时进行映射，在前面建立映射关系时，只要前缀和出现就进行映射，但是本题需要注意到要求最长的子数组，如果出现下面抽象图描述的情况时，就不需要更新下标：

因为当前哈希表中存储的是前缀和与下标，而这个前缀和意味着是sum-k，如果sum-k所在的区间长，则对应的和为0的子数组越短，所以在上图中len1<len2，说明len1对应的和为0的子数组长度大于len2对应的和为0的子数组长度

同样，如果前缀和默认为0，此时也需要单独进行特殊处理，但是注意，此时哈希表第二个位置是下标，如果前缀和默认为0，说明整个数组的长度刚好就是最长的子数组，其区间就是[0, n - 1]，所以前缀和默认为0时，映射的下标位置为-1

本题最后需要考虑的就是如何计算长度，同样看下面的示意图：

可以看到如果x位置的前缀和为前四个元素之和，那么后面的4个元素的长度才是需要的子数组的长度，因为整个区间为(x, i]，所以其长度为i - x

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution525
{
public:
    int findMaxLength(vector<int> &nums)
    {
        unordered_map<int, int> cnt;
        cnt[0] = -1;

        // 在数组中找前缀和为sum的最长子数组
        int sum = 0;
        int ret = 0;
        for (int i = 0; i < nums.size(); i++)
        {
            // 求前缀和
            // 注意遇到0时取-1
            sum += nums[i] == 0 ? -1 : 1;

            // 哈希表中存储的是前缀和，当遇到了前缀和为sum时就更新当前长度
            if (cnt.find(sum) != cnt.end())
            {
                ret = max(ret, i - cnt[sum]);
            }
            else 
            {
                // 如果哈希表中不存在，说明是第一次出现，更新映射
                // 第二次找到的和为0子数组长度一定没有第一次找到的和为0子数组长度长
                cnt[sum] = i;
            }
        }

        return ret;
    }
};

力扣1314.矩阵区域和

力扣1314.矩阵区域和

问题描述：

Quote

给你一个\(m \times n\)的矩阵mat和一个整数k，请你返回一个矩阵answer，其中每个answer[i][j]是所有满足下述条件的元素mat[r][c]的和：

  1. i - k <= r <= i + k
  2. j - k <= c <= j + k
  3. (r, c)在矩阵内

示例 1：

C++
1
2
输入：mat = [[1,2,3],[4,5,6],[7,8,9]], k = 1
输出：[[12,21,16],[27,45,33],[24,39,28]]

示例 2：

C++
1
2
输入：mat = [[1,2,3],[4,5,6],[7,8,9]], k = 2
输出：[[45,45,45],[45,45,45],[45,45,45]]

思路分析：

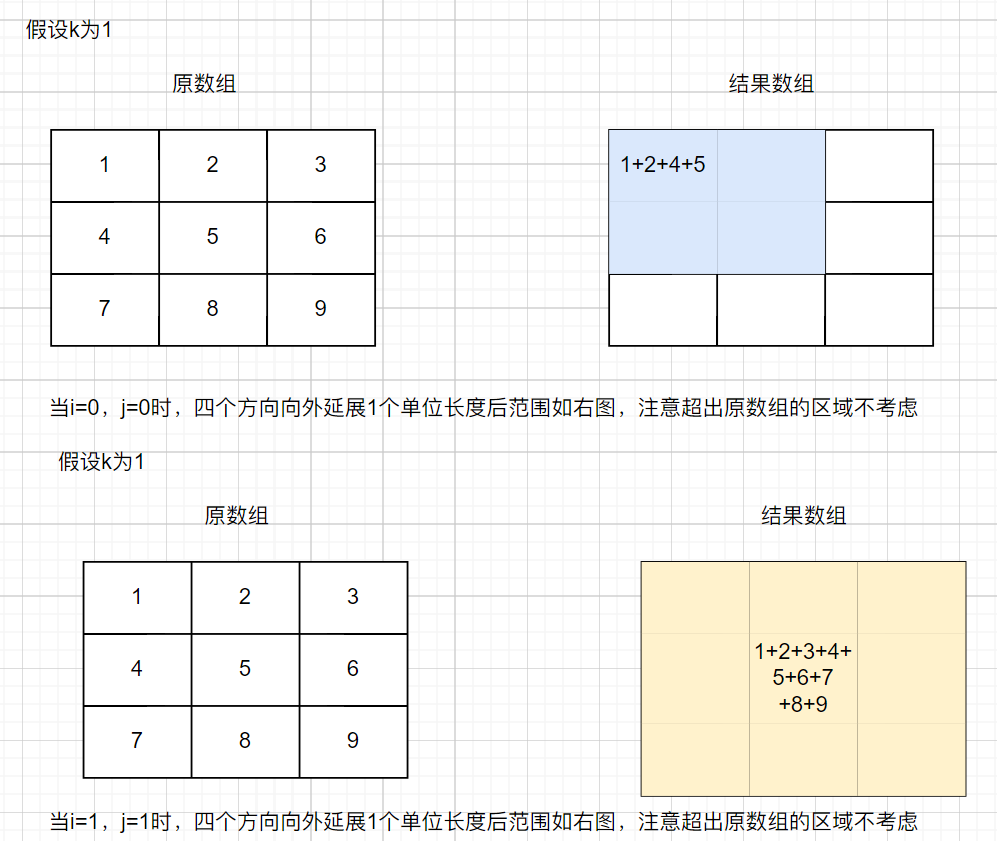
本题的关键就是理解题意以及对边界的处理，剩余的就是二维前缀和的基本构建和使用。本题的题意就是根据k值以当前下标所在位置为基准向四个方向延展k个长度，求出延展后的区域中的所有元素之和放到当前下标的位置

示意图如下：

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution
{
public:
    vector<vector<int>> matrixBlockSum(vector<vector<int>> &mat, int k)
    {
        int m = mat.size();
        int n = mat[0].size();
        // 构建前缀和数组
        vector<vector<int>> sum(m + 1, vector<int>(n + 1));

        for (int i = 1; i <= m; i++)
        {
            for (int j = 1; j <= n; j++)
            {
                sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + mat[i - 1][j - 1];
            }
        }

        // 使用前缀和数组
        int x1 = 0, x2 = 0, y1 = 0, y2 = 0;
        vector<vector<int>> ans(m, vector<int>(n));
        for (int i = 0; i < m; i++)
        {
            for (int j = 0; j < n; j++)
            {
                x1 = max(0, i - k) + 1;
                y1 = max(0, j - k) + 1;
                x2 = min(m - 1, i + k) + 1;
                y2 = min(n - 1, j + k) + 1;

                // 求和
                ans[i][j] = sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1];
            }
        }

        return ans;
    }
};