跳转至

模拟

约 4125 个字 432 行代码 4 张图片 预计阅读时间 19 分钟

介绍

模拟算法就是根据题目描述构建思路，通过代码实现题目描述的效果，模拟类题目最考验的就是做题者的代码能力。一般模拟类的题目分为两种：

  1. 暴力模拟
  2. 找规律

示例题目

力扣1576.替换所有的问号

问题描述：

Quote

给你一个仅包含小写英文字母和?字符的字符串s，请你将所有的?转换为若干小写字母，使最终的字符串不包含任何连续重复的字符。

注意：你不能修改非'?'字符。

题目测试用例保证 除?字符 之外，不存在连续重复的字符。

在完成所有转换（可能无需转换）后返回最终的字符串。如果有多个解决方案，请返回其中任何一个。可以证明，在给定的约束条件下，答案总是存在的。

示例 1：

C++
1
2
3
输入：s = "?zs"
输出："azs"
解释：该示例共有 25 种解决方案，从 "azs" 到 "yzs" 都是符合题目要求的。只有 "z" 是无效的修改，因为字符串 "zzs" 中有连续重复的两个 'z' 。

示例 2：

C++
1
2
3
输入：s = "ubv?w"
输出："ubvaw"
解释：该示例共有 24 种解决方案，只有替换成 "v" 和 "w" 不符合题目要求。因为 "ubvvw" 和 "ubvww" 都包含连续重复的字符。

思路分析：

分析本题的题意，模拟题的第一步就是先弄清题目的要求，本题题意就是将所有的问号替换成一个小写字母，但是这个小写字母必须不能与其左侧的字符（如果存在）相同或者其右侧的字符相同（如果存在）

接着就是第二步，在草稿纸上分析本题是暴力模拟还是找规律，从一般情况入手：例如字符串bac?zabc，对于?来说，可以替换的字符有a、b、d、……、y，可以看到本题只需要遍历一遍字符串，在出现?位置再依次枚举26个小写字母，判断其与前一个字符或后一个字符是否相等，如果不相等，则表示该字符可以作为替换字符

但是，在比较过程中需要注意两种特殊情况：第一种是?出现在字符串开始，第二种是?出现在字符串末尾。对于第一种情况来说，只需要使枚举的字符比较后一个字符即可；对于第二种情况，只需要让枚举的字符比较前一个字符即可

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution1576
{
public:
    string modifyString(string s)
    {
        for (int i = 0; i < s.size(); i++)
        {
            if (s[i] == '?')
            {
                for (char j = 'a'; j <= 'z'; j++)
                {
                    if ((i - 1 < 0 || j != s[i - 1]) && (i + 1 >= s.size() || j != s[i + 1]))
                    {
                        s[i] = j;
                        break;
                    }
                }
            }
        }

        return s;
    }
};

相关题目

力扣495.提莫攻击

力扣495.提莫攻击

问题描述：

Quote

在《英雄联盟》的世界中，有一个叫 “提莫” 的英雄。他的攻击可以让敌方英雄艾希（编者注：寒冰射手）进入中毒状态。

当提莫攻击艾希，艾希的中毒状态正好持续duration秒。

正式地讲，提莫在t发起攻击意味着艾希在时间区间[t, t + duration - 1]（含t和t + duration - 1）处于中毒状态。如果提莫在中毒影响结束 前 再次攻击，中毒状态计时器将会重置，在新的攻击之后，中毒影响将会在duration秒后结束。

给你一个非递减的整数数组timeSeries，其中timeSeries[i]表示提莫在timeSeries[i]秒时对艾希发起攻击，以及一个表示中毒持续时间的整数 duration。

返回艾希处于中毒状态的总秒数。

示例 1：

C++
1
2
3
4
5
6
输入：timeSeries = [1,4], duration = 2
输出：4
解释：提莫攻击对艾希的影响如下：
- 第 1 秒，提莫攻击艾希并使其立即中毒。中毒状态会维持 2 秒，即第 1 秒和第 2 秒。
- 第 4 秒，提莫再次攻击艾希，艾希中毒状态又持续 2 秒，即第 4 秒和第 5 秒。
艾希在第 1、2、4、5 秒处于中毒状态，所以总中毒秒数是 4 。

示例 2：

C++
1
2
3
4
5
6
输入：timeSeries = [1,2], duration = 2
输出：3
解释：提莫攻击对艾希的影响如下：
- 第 1 秒，提莫攻击艾希并使其立即中毒。中毒状态会维持 2 秒，即第 1 秒和第 2 秒。
- 第 2 秒，提莫再次攻击艾希，并重置中毒计时器，艾希中毒状态需要持续 2 秒，即第 2 秒和第 3 秒。
艾希在第 1、2、3 秒处于中毒状态，所以总中毒秒数是 3 。

思路分析：

分析本题的题意，本题的目标是获取到艾希一共受到的中毒时长，但是这个时长并不是简单得累加，根据题目描述，如果在中毒过程中提莫又一次攻击，中毒时长会重置（即中毒时长计数重新从1开始）

根据前面的分析，本题根据「是否在中毒过程中又一次受到攻击」分为两种情况：

  1. 相邻攻击差值大于等于duration
  2. 相邻攻击差值小于duration

对于第一种情况来说，因为相邻攻击差值大于等于duration，所以一定不会重置中毒时长，所以只需要简单累加技能持续时间duration即可

对于第二种情况来说，因为相邻攻击差值小于duration，所以一定存在重置中毒时长，而重置中毒时长的位置就是紧接着发动攻击的时间点，此时计时器会被重新更新为1，假设这个计时器为count，所以可以推出count=下一次发动攻击的时间点-上一次发动攻击的时间点，所以可以推出在中毒时长重置的时间点到上一次发动攻击的时间点中间的间隔就是中毒时长

最后，不论是第一种情况还是第二种情况，在最后一次受到攻击后，中毒效果会一直持续到结束

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution495_1
{
public:
    int findPoisonedDuration(vector<int> &timeSeries, int duration)
    {
        int time = 0;
        for (int i = 0; i < timeSeries.size(); i++)
        {
            if (i + 1 < timeSeries.size() && timeSeries[i + 1] - timeSeries[i] >= duration)
            {
                time += duration;
            }
            else if (i + 1 < timeSeries.size() && timeSeries[i + 1] - timeSeries[i] < duration)
            {
                time += timeSeries[i + 1] - timeSeries[i];
            }
        }

        // 最后一次攻击会持续到结尾
        time += duration;

        return time;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution495_2
{
public:
    int findPoisonedDuration(vector<int> &timeSeries, int duration)
    {
        int time = 0;
        for (int i = 1; i < timeSeries.size(); i++)
        {
            if (timeSeries[i] - timeSeries[i - 1] >= duration)
            {
                // 第一种情况
                time += duration;
            }
            else
            {
                time += timeSeries[i] - timeSeries[i - 1];
            }
        }

        // 最后一种情况
        time += duration;

        return time;
    }
};

力扣6.Z字形变换

力扣6.Z字形变换

问题描述：

Quote

将一个给定字符串s根据给定的行数numRows，以从上往下、从左到右进行Z字形排列。

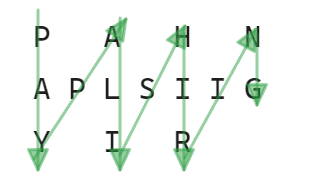
比如输入字符串为"PAYPALISHIRING"行数为3时，排列如下：

C++
1
2
3
P   A   H   N
A P L S I I G
Y   I   R
之后，你的输出需要从左往右逐行读取，产生出一个新的字符串，比如：PAHNAPLSIIGYIR

请你实现这个将字符串进行指定行数变换的函数：

string convert(string s, int numRows);

示例 1：

C++
1
2
输入：s = "PAYPALISHIRING", numRows = 3
输出："PAHNAPLSIIGYIR"

示例 2：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
输入：s = "PAYPALISHIRING", numRows = 4
输出："PINALSIGYAHRPI"
解释：
P     I    N
A   L S  I G
Y A   H R
P     I
```c++

示例 3：

```c++
输入：s = "A", numRows = 1
输出："A"

思路分析：

分析题目，本题所谓的Z字形排列，实际上如下图所示：

将排列后的结果依次遍历得到一个新字符串PAHNAPLSIIGYIR

  1. 解法1：暴力模拟

    观察模拟过程，首先需要构建一个二维矩阵，先第一列从上向下一次存储字符，再从下向斜上存储字符，接着重复前面的两个操作直到字符全部用完，可以看到整个过程中涉及到一种周期性的问题，其中前面两个步骤就是一个周期，计算出周期数就可以确定二维矩阵的列数。但是如果不想计算周期，也可以简单粗暴得将列的个数设置为字符串的长度，因为字符串会蜿蜒，所以原始字符串的长度一定会比存储需要的列多。这个题目字符串最长的长度为1000，所以最多需要1000列。具体分析见下面的单独分析

  2. 解法2：找规律

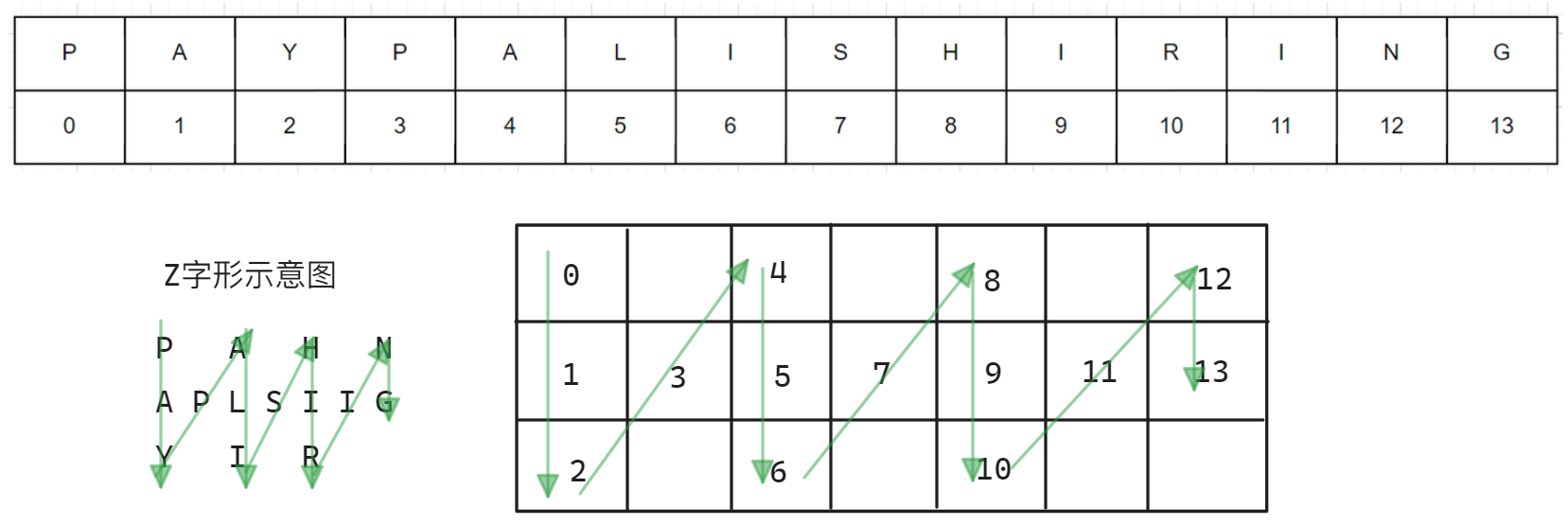
    对于这种复杂的题目，一般都会存在某一种规律，本题就是如此。在草稿纸上构建出Z字形排列后的矩阵，但是矩阵中并不实际填写字符，而是用对应的下标代替，如下图所示：

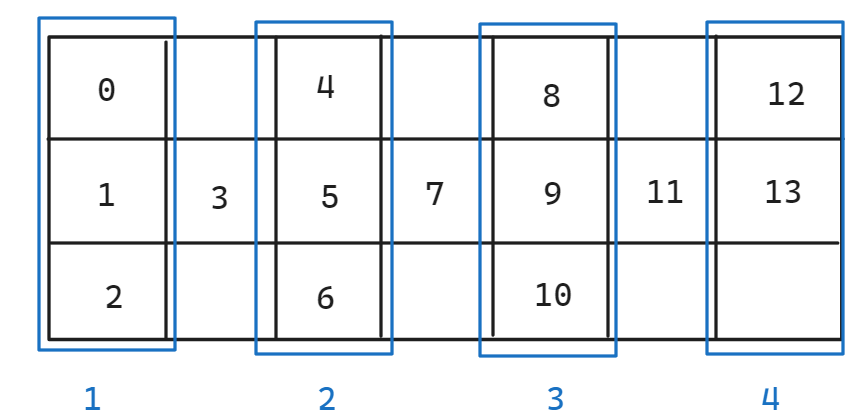
    从下标可以看到，第一行和最后一行的每一列数值间隔为4，如下图所示：

    为了通用性，考虑将其使用一个表达式表示，假设该值为d，先观察矩阵的第1列和第2列，第1行第2列的4就是前面出现的字符个数，而这个字符个数根据模拟的过程可以推出：图中蓝色相邻两列（框选的第1列和第2列）间隔中的一列总会有上下各一格空出，所以可以得出矩阵相邻两列的元素总和为\(2 \times 3 - 2\)，其中第一个2表示矩阵相邻两列一行两个元素，3表示矩阵总行数，第二个2表示上下各空出的一个空格。根据前面的规律推出公差公式为\(2 \times 总共行数 - 2\)

    根据上面的公差公式和字符总个数就可以一次枚举出第一行和最后一行的字符

    接着考虑除了第一行和最后一行的中间行，对于框选的列来说，其相差公差d的列与第一行和最后一行规律一致，而框选两列中间的数值也各自相差公差d，假设中间行为第k行，则有起始位置分别为k和d-k，再各自增加公差d即可。注意在填充过程中需要考虑当前下标是否超过字符总个数

    本题最后还需要注意，如果给的参数numRows为1，则直接返回原字符串

暴力模拟思路（了解）

有了上面的规律，可以直到矩阵第一列和第二列一共存储的字符个数是\(num = 2 \times 总共行数 - 2\)个，而因为从上向下，从下斜向上为一个周期，所以对于整个字符串来说，假设字符串元素个数为n，一共存在\(\lceil \frac{n}{num} \rceil\)（其中的\(\lceil \text{ } \rceil\)为向上取整符号），而因为每一次周期为numRows - 1列，所以得出最后二维矩阵需要的列数col为\(\lceil \frac{n}{num} \rceil \cdot (numRows - 1)\)

根据前面的描述，暴力解法需要依次填充矩阵，首先就需要构建矩阵，接着按照下面的规律进行，假设行下标为i，列下标为j：

  1. 竖向填充列，i++，直到i == numRows - 1
  2. 斜向上填充，i--, j++，直到i >= 1
  3. 重复前面的两步，直到遍历完所有的字符串
  4. 按行按列打印矩阵

Note

注意，此处假设最后一个周期也是一个完整周期

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
class Solution6_1
{
public:
    string convert(string s, int numRows)
    {
        if(numRows == 1)
        {
            return s;
        }
        // 获取字符串的长度
        int sz = s.size();
        // 获取周期
        int cycle = ceil((float)sz / (2 * numRows - 2)) * (numRows - 1);
        // 构建二维矩阵
        vector<vector<char>> matrix(numRows, vector<char>(cycle));

        int i = 0;
        int j = 0;
        int k = 0;
        // 填充二维矩阵
        while (k < sz)
        {
            // 填充竖向列
            while (i < numRows)
            {
                if (k >= sz)
                    break;
                matrix[i][j] = s[k++];
                i++;
            }

            i -= 2;
            // 填充斜向上
            while (i > 0)
            {
                if (k >= sz)
                    break;
                j++;
                matrix[i][j] = s[k++];
                i--;
            }

            j++;
        }

        // 遍历二维矩阵
        string ret;
        for (auto &v : matrix)
        {
            for (auto &ch : v)
            {
                if (ch == '\0')
                    continue;
                ret += ch;
            }
        }

        return ret;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution6_2
{
public:
    string convert(string s, int numRows)
    {
        if (numRows == 1)
        {
            return s;
        }

        // 获取字符串长度
        int sz = s.size();
        // 获取公差
        int d = 2 * numRows - 2;

        string ret;
        // 处理第一行
        for (int i = 0; i < sz; i += d)
        {
            ret += s[i];
        }

        // 处理中间行
        for (int k = 1; k < numRows - 1; k++)
        {
            for (int x = k, y = d - k; x < sz || y < sz; x += d, y += d)
            {
                if (x < sz)
                {
                    ret += s[x];
                }
                if (y < sz)
                {
                    ret += s[y];
                }
            }
        }

        // 处理最后一行
        for (int i = numRows - 1; i < sz; i += d)
        {
            ret += s[i];
        }

        return ret;
    }
};

力扣59.螺旋矩阵 II

力扣59.螺旋矩阵 II

问题描述：

Quote

给你一个正整数n，生成一个包含1到\(n^2\)所有元素，且元素按顺时针顺序螺旋排列的\(n \times n\)正方形矩阵matrix。

示例 1：

C++
1
2
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2：

C++
1
2
输入：n = 1
输出：[[1]]

思路分析：

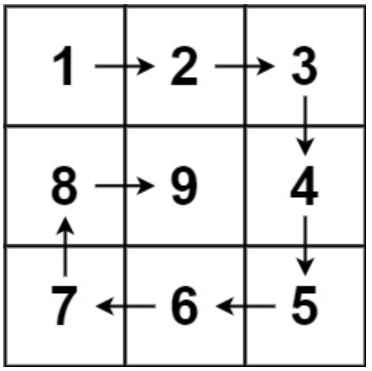
分析本题，可以看到本题需要根据给定的数值生成一个按照顺时针方向填充的矩阵，再返回该矩阵

本题就是暴力模拟的过程，但是要找到一定的规律，首先看正方形最外圈，上边缘就是改变列，但是不改变行，接着就是改变行不改变列，再接着就是改变列不改变行，最后改变行不改变列，从而构成一个正方形的四条边。所以根据这个思路只需要编写循环依次模拟即可，但是这个问题的难点就在于边界处理，一定要保证在整个填充过程中不重复填充某一个位置

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution59
{
public:
    vector<vector<int>> generateMatrix(int n)
    {
        // 处理结果
        vector<vector<int>> ret(n);
        for (auto &v: ret)
            v.resize(n);
        int count = 1;
        int left = 0, top = 0;
        int right = n - 1, bottom = n - 1;
        while (left <= right && top <= bottom)
        {
            // 上边缘
            for (int i = left; i <= right; i++)
                ret[top][i] = count++;
            top++;
            // 右边缘
            for (int i = top; i <= bottom; i++)
                ret[i][right] = count++;
            right--;
            // 下边缘
            for (int i = right; i >= left; i--)
                ret[bottom][i] = count++;
            bottom--;
            // 左边缘
            for (int i = bottom; i >= top; i--)
                ret[i][left] = count++;
            left++;
        }

        return ret;
    }
};

力扣54.螺旋矩阵

类似于力扣59题：力扣54.螺旋矩阵

关键步骤：

注意本题因为没有固定是正方形，所以需要判断是否存在下一行以及下一列

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
class Solution54
{
public:
    vector<int> spiralOrder(vector<vector<int>> &matrix)
    {
        // 处理结果
        vector<int> ret;
        // 获取行和列
        int m = matrix.size();
        int n = matrix[0].size();
        // 定义上下左右边
        int left = 0;
        int right = n - 1;
        int top = 0;
        int bottom = m - 1;

        while (top <= bottom && left <= right)
        {
            // 处理第一行
            for (int i = left; i <= right; i++)
            {
                ret.push_back(matrix[left][i]);
            }
            // 第一行处理完毕
            top++;

            // 处理第一列
            for (int i = top; i <= bottom; i++)
            {
                ret.push_back(matrix[i][right]);
            }
            // 第一列处理完毕
            right--;

            // 处理第二行
            // 需要判断是否还有第二行
            if (top <= bottom)
            {
                for (int i = right; i >= left; i--)
                {
                    ret.push_back(matrix[bottom][i]);
                }
                // 第二行处理完毕
                bottom--;
            }

            // 处理第二列
            // 需要判断是否还有第二列
            if (left <= right)
            {
                for (int i = bottom; i >= top; i--)
                {
                    ret.push_back(matrix[i][left]);
                }
                left++;
            }
        }

        return ret;
    }
};

力扣38.外观数列

力扣38.外观数列

Quote

「外观数列」是一个数位字符串序列，由递归公式定义：

countAndSay(1) = "1"

countAndSay(n)是countAndSay(n-1)的行程长度编码。

行程长度编码（RLE）是一种字符串压缩方法，其工作原理是通过将连续相同字符（重复两次或更多次）替换为字符重复次数（运行长度）和字符的串联。例如，要压缩字符串3322251，我们将33用23替换，将222用32替换，将5用15替换并将1用11替换。因此压缩后字符串变为23321511。

给定一个整数n，返回外观数列的第n个元素。

示例 1：

C++
1
2
3
4
5
6
7
输入：n = 4
输出："1211"
解释：
countAndSay(1) = "1"
countAndSay(2) = "1" 的行程长度编码 = "11"
countAndSay(3) = "11" 的行程长度编码 = "21"
countAndSay(4) = "21" 的行程长度编码 = "1211"

示例 2：

C++
1
2
3
4
输入：n = 1
输出："1"
解释：
这是基本情况。

思路分析：

本题首先需要知道何为「行程长度编码」，根据题目的描述，在按照「行程长度编码」编写的字符串中，相邻的两个字符中第一个字符表示第二个字符出现的个数

明白了「行程长度编码」之后再看题目要求的结果：「给定一个整数n，返回外观数列的第n个元素」，其本质就是返回将字符串s = "1"进行4次编码，返回第4次编码的结果

关键步骤：

因为本题需要统计相同字符的个数，所以可以考虑使用双指针遍历，假设字符串为s，两个指针分别是left和right，当s[left] == s[right]时，只需要改变right，否则让left到right的位置，而要计算right和left中间的字符个数，只需要使用right-left即可，因为right在每一次找到第一个与left位置不同的字符时才会停下，所以本质就是左闭右开区间，即[left, right)

需要注意，在遍历过程中需要拼接使用编码后的字符串，对于数值来说，可以考虑使用一个to_string()函数对个数转换

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution38_1
{
public:
    string countAndSay(int n)
    {
        if (n == 1)
        {
            return "1";
        }

        string ret = countAndSay(n - 1);
        string temp;
        temp.clear();
        for (int left = 0, right = 0; right < ret.size(); left = right)
        {
            while (ret[left] == ret[right])
            {
                right++;
            }

            temp += to_string(right - left) + ret[left];
        }

        ret = temp;

        return ret;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution38_2
{
public:
    string countAndSay(int n)
    {
        string ret = "1";
        for (int i = 1; i < n; i++)
        {
            string temp;
            // 统计个数
            for (int left = 0, right = 0; right < ret.size(); left = right)
            {
                // 持续寻找相同的字符
                while (right < ret.size() && ret[left] == ret[right])
                {
                    right++;
                }

                // 更新字符串
                temp += to_string(right - left) + ret[left];
            }
            ret = temp;
        }
        return ret;
    }
};

力扣1419.数青蛙

力扣1419.数青蛙

问题描述：

Quote

给你一个字符串croakOfFrogs，它表示不同青蛙发出的蛙鸣声（字符串croak）的组合。由于同一时间可以有多只青蛙呱呱作响，所以croakOfFrogs中会混合多个croak。

请你返回模拟字符串中所有蛙鸣所需不同青蛙的最少数目。

要想发出蛙鸣croak，青蛙必须依序输出c, r, o, a, k这 5 个字母。如果没有输出全部五个字母，那么它就不会发出声音。如果字符串 croakOfFrogs 不是由若干有效的croak`字符混合而成，请返回-1。

示例 1：

C++
1
2
3
输入：croakOfFrogs = "croakcroak"
输出：1 
解释：一只青蛙 “呱呱” 两次

示例 2：

C++
1
2
输入：croakOfFrogs = "crcoakroak"
输出：2
解释：最少需要两只青蛙，“呱呱” 声用黑体标注

第一只青蛙"crcoakroak"

第二只青蛙"crcoakroak"

示例 3：

C++
1
2
3
输入：croakOfFrogs = "croakcrook"
输出：-1
解释：给出的字符串不是 "croak" 的有效组合。

思路分析：

先了解题目意思，每一只青蛙都会叫croak，但是并不是必须一只青蛙叫完，另外一只青蛙才能叫，比如题目的示例2，在示例2中的字符串中，可以拆出两个croak，代表有两只青蛙同时叫

除了示例2的情况外，还存在一种情况，因为青蛙叫完croak后可以再接着叫，所以如果存在一个字符串s = crcoakroakcroak，因为题目要求青蛙的最少树木，则此时依旧是两只青蛙在叫，因为第一只青蛙在第一次叫完croak后，第二只青蛙还在叫，所以第一只青蛙可以接着叫最后一个croak

最后，对于示例3，如果字符串中存在一个非croak的子字符串，则说明并没有青蛙在叫，返回-1

根据上面的题目分析，可以得出本题需要一个哈希表来统计croak中的每一个字符在所给字符串中出现的次数，以此来判断某一个子字符串是否匹配croak，但是，这里不是先遍历整个字符串进行计数，观察示例2，当一个青蛙开始叫了，其叫声开始的第一个字符c就是一个标志，接着依次遍历所给的字符串判断当前字符的前一个字符是否存在且只出现一次，如果存在且出现一次就说明有青蛙在叫，否则就说明没有青蛙在叫，所以哈希表中本质存储的就是所给字符串的当前字符的上一个字符出现的次数

根据上面的思路，此时就可以分出两种情况：

  1. 当青蛙叫到了r、o、a和k，则说明需要判断其前一个字符是否出现，如果出现让前一个字符的个数减1，当前字符加1，否则返回-1
  2. 当青蛙叫到了c，则说明有一只青蛙开始叫。但是此时需要注意，这个青蛙可以是一只新的青蛙，也可以是上一个已经叫完的青蛙，所以还需要判断c的前一个字符k出现的次数是否为0，如果为0，说明是一只新青蛙，如果不为0，则说明可以有一只已经叫完的青蛙继续叫，这样才可以确保返回的青蛙数目最小

在上面的两种情况中，因为需要访问上一个字符，所以可以考虑将croak与其对应的下标映射到一个哈希表中方便查找

最后，如果除了k字符存储着青蛙的最少数目外，其他字符如果数目不为0，说明不为0的字符一定出现了两次及以上，此时就说明该字符串一定存在非croak的子串

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution
{
public:
    int minNumberOfFrogs(string croakOfFrogs)
    {
        string s = "croak";
        int sz = s.size();
        // 创建哈希表用于字符个数的映射
        vector<int> hash(sz);

        // 创建哈希表用于下标映射
        unordered_map<char, int> index;
        for (int i = 0; i < s.size(); i++)
        {
            index[s[i]] = i;
        }

        // 遍历所给字符串
        for (auto ch : croakOfFrogs)
        {
            if (ch == 'c')
            {
                // 判断k字符个数是否为0
                if (hash[index[ch] + sz - 1])
                {
                    hash[index[ch] + sz - 1]--;
                }
                hash[index[ch]]++;
            }
            else
            {
                // 其他四个字符
                if (hash[index[ch] - 1] == 0)
                    return -1;
                hash[index[ch] - 1]--;
                hash[index[ch]]++;
            }
        }

        // 结束后判断是否存在除k以外的字符的个数非0
        for (int i = 0; i < hash.size() - 1; i++)
            if (hash[i] != 0)
                return -1;

        return hash[index['k']];
    }
};