跳转至

位运算

约 4206 个字 578 行代码 15 张图片 预计阅读时间 21 分钟

介绍

在部分算法题中，使用位运算可能可以更好得达到题目的要求，在C/C++中，常见的位运算符有下面几种：

  1. 左移运算<<
  2. 右移运算>>
  3. 按位与&
  4. 按位或|
  5. 按位异或^
  6. 按位取反~

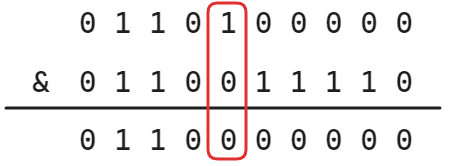
其中，对于按位与来说，其规律就是「有0则0」；对于按位或来说，其规律就是「有1则1」；对于按位异或来说，其基本规律就是「相同则0，相异则1」，实际上按位异或还可以理解为「无进位相加」

下面重点解释一下按位异或的「无进位相加」

在二进制加法计算中，1 + 1 = 10，此时结果10的高位1属于进位的结果，在上图中1 ^ 1 = 0，而其他的计算都不改变，例如1 ^ 0 = 1，0 ^ 0 = 0且都等于1 + 0和0 + 0

所以按位异或可以理解为没有进位版本的加法，即「无进位相加」

常见的位运算操作

介绍完常见的位运算符后，下面介绍常见的位运算操作：

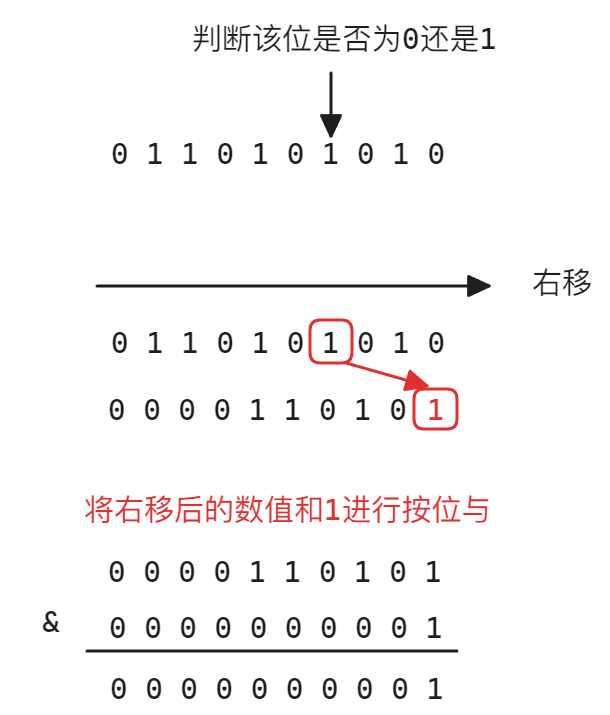
  1. 给定一个数n，确定其二进制表示中的第i位是0还是1

    思路：(n >> i) & 1

    原理：

    Note

    注意，二进制最低位下标为0，依次向左增大，所以当i为0时，则上面的计算式(n >> i) & 1就变为n & 1，即原数值，所以当i为1时，就是移动低第二位

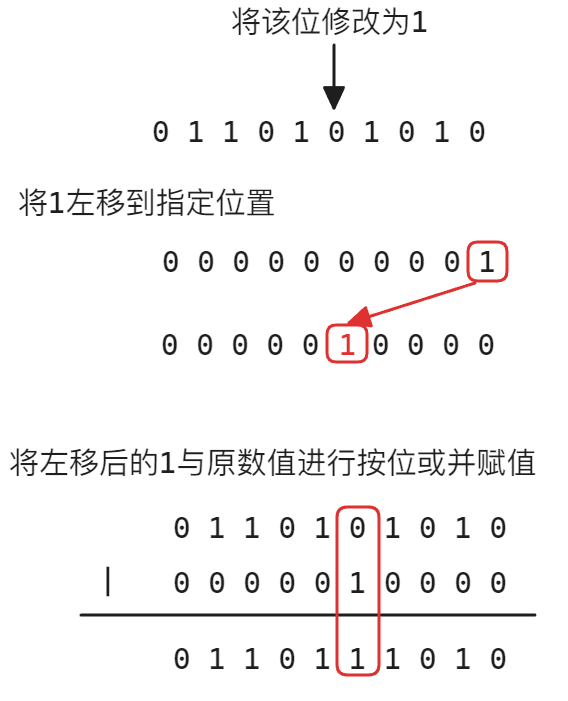
  2. 给定一个数n，将其二进制表示中的第i位的修改为1

    思路：n |= (1 << i)

    原理：

  3. 给定一个数n，将其二进制表示中的第i位的修改为0

    思路：n &= (~(1 << i))

    原理：

  4. 位图思想：前面的三种方式如果看过位图部分就会感觉很熟悉，其实就是位图的基本操作

  5. 提取一个数n的二进制表示中最右侧的1（也被称为lowbit）

    思路：n & (-n)

    原理：

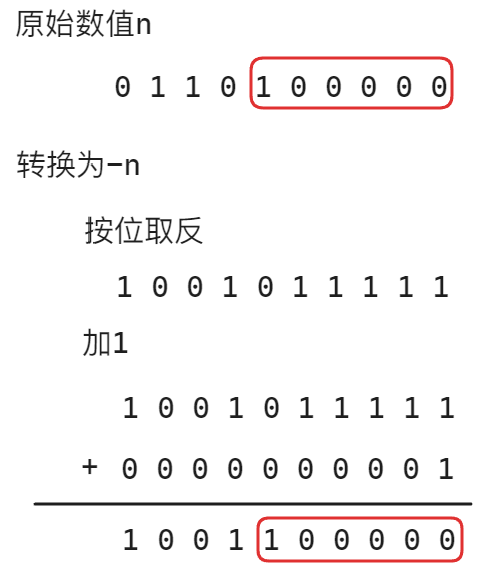
    理解本思路的原理，就需要理解-n的原理，计算一个正数的负数的方式为按位取反加1，过程如下：

    可以看到，-n的结果中，从某一位开始，该位左侧的二进制与原数值刚好是按位取反的结果，该位右侧的二进制与原数值相同

    接着将-n与原数值按位与就可以得到下面的结果：

    可以看到，原数值n二进制表示中最低位的1因为其-n左侧的二进制是原数值的按位取反结果，所以按位与之后结果只会为0，而右侧不变，既然是最低位的1，所以该1的右侧绝对都是0，最后获取到的数值只会在原数值的二进制表示中最低位为1的位置为1

  6. 将一个数n的二进制表示中最右侧的1变为0（Brian Kernighan算法）

    思路：n & (n - 1)

    原理：

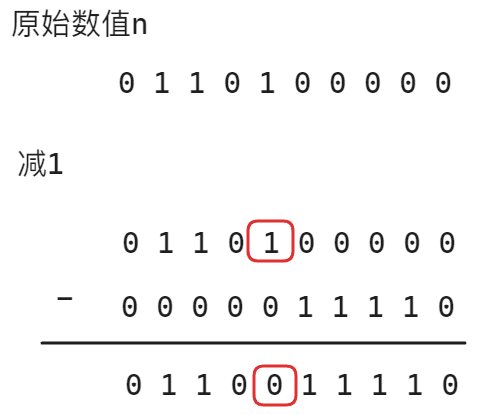
    理解本思路的原理，就需要理解n - 1的原理，一个数值减1，就代表其二进制最低位需要减1，但是如果最右侧的1不在原数值二进制表示中的最低位，此时就需要向前借位，一直会借到最右侧的1为止，过程如下：

    所以n - 1的本质就是让最右侧的1因为借位变为0，达到从被借位的位置开始，其左侧的二进制与原数的二进制相同，其右侧的二进制位与原数的二进制刚好为按位取反的结果

    接着再与原数值按位与，就可以保证最右侧的1变为0，而其右侧的0因为是按位与，使得最后的结果依旧为0，左侧因为保持不变，所以按位与也不会改变原数值的二进制，过程如下：

    关于Brian Kernighan算法

    Brian Kernighan算法发布在1988年出版的The C Programming Language (Second Edition)的练习中（由Brian W. Kernighan和 Dennis M. Ritchie 编写），但是 Donald Knuth在2006年4月19日指出，该方法第一次是由Peter Wegner在1960年的CACM3上出版。可以在上述书籍中找到更多位操作的技巧

  7. 异或相关操作，假设一个数值为a

    1. a ^ a = 0
    2. a ^ 0 = a
    3. a ^ b ^ c = a ^ (b ^ c)（异或运算的结合律）

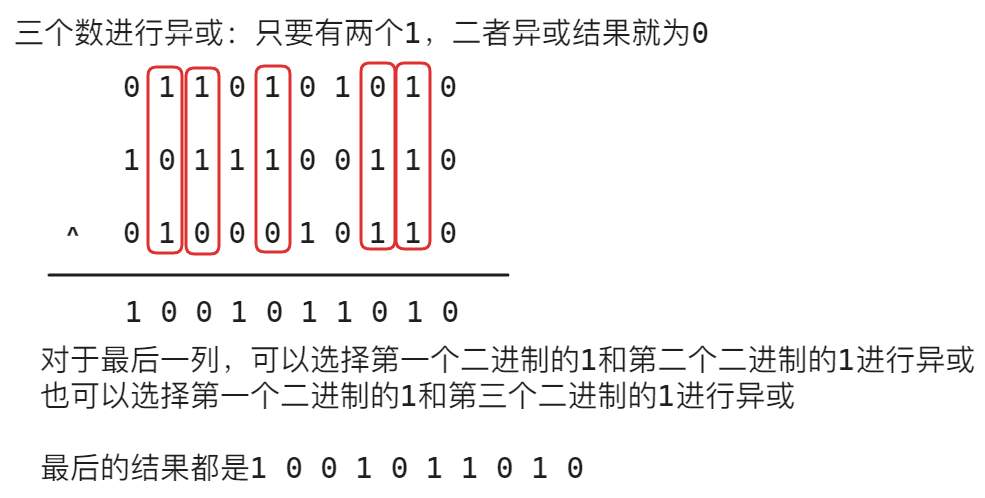
    其中，前面两个操作是异或运算的基本操作，而第三种，正是因为有结合律，就可以确保多个数值异或运算过程中不需要考虑计算顺序，其原理就是利用了异或运算的「无进位加法」的特点，例如下面的过程：

Note

上面因为涉及到各种运算符的结合，所以少不了需要考虑运算符的优先级，但是直接记优先级表就会很繁琐，为了减轻工作量可以直接对需要先计算的表达式用括号包裹

示例题目

力扣461.汉明距离

问题描述：

Quote

两个整数之间的汉明距离指的是这两个数字对应二进制位不同的位置的数目。

给你两个整数x和y，计算并返回它们之间的汉明距离。

示例 1：

C++
1
2
3
4
5
6
7
输入：x = 1, y = 4
输出：2
解释：
1   (0 0 0 1)
4   (0 1 0 0)
    ↑   ↑
上面的箭头指出了对应二进制位不同的位置。

示例 2：

C++
1
2
输入：x = 3, y = 1
输出：1

思路分析：

本题要求的是两个数字对应的二进制位不同的位置的个数，所以可以考虑使用异或运算，因为异或运算的结果是相异为1，相同为0，对于二进制位不同时，该位结果就会为1，否则就为0，最后统计异或运算结果中1的个数即可

  1. 解法1：内置库函数统计异或运算结果中1的个数
  2. 解法2：移位判断指定位是否为0

  3. 解法3：利用n&(n-1)结合计数器

    解法3本质是尽可能减少统计1的过程的时间消耗，基本思路与解法2还是一致的，下面看解法3如何优化解法2的时间消耗：

    在解法2中，如果两个1中有非常多的0，则需要一直移位，实际上只需要判断每一个1的位置就可以

    使用n&(n-1)本质就是利用其会将指定数的二进制表示中的1改变为0，如果所有1变为了0，则结果十进制为0，而每一次更改就代表遇到一个1，更新计数器，整个过程可以发现是个循环，而循环的终止条件就是判断n是否为0

Note

注意，第一种解法中使用的库函数是int __builtin_popcount(size_t num)，这个函数是GCC提供的一个内建函数，用于计算一个整数的二进制表示中有多少个1（即计算汉明重量或人口计数）。这个函数可以用于优化代码，因为它通常会被编译为高效的硬件指令。

其基本使用如下：

C++
1
2
3
4
5
6
7
8
9
#include <iostream>
using namespace std;

int main() {
    int num = 29; // 二进制表示为11101
    int count = __builtin_popcount(num);
    cout << count << endl;  // 4
    return 0;
}

参考代码：

C++
1
2
3
4
5
6
7
8
class Solution461_1
{
public:
    int hammingDistance(int x, int y)
    {
        return __builtin_popcount(x ^ y);
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution461_2
{
public:
    int hammingDistance(int x, int y)
    {
        // 统计个数
        int count = 0;
        // 二者异或
        int ans = x ^ y;

        // 找出一共多少个1
        for (int i = 0; i < 32; i++)
        {
            if ((ans >> i) & 1)
            {
                count++;
            }
        }
        return count;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution461_3
{
public:
    int lowbit(int num)
    {
        return num & (num - 1);
    }

    int hammingDistance(int x, int y)
    {
        // 统计个数
        int count = 0;
        // 二者异或
        int ans = x ^ y;

        // 找出一共多少个1
        while (ans)
        {
            ans = lowbit(ans);
            count++;
        }
        return count;
    }
};

相关题目

力扣338.比特位计数

类似于461题：力扣338.比特位计数

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution338
{
public:
    vector<int> countBits(int n)
    {
        vector<int> ret;
        for (int i = 0; i <= n; i++)
        {
            int count = 0;
            int temp = i;
            // 位运算
            while (temp)
            {
                temp = temp & (temp - 1);
                count++;
            }

            ret.push_back(count);
        }

        return ret;
    }
};

力扣191.位1的个数

类似于461题：力扣191.位1的个数

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution191
{
public:
    int lowbit(int num)
    {
        return num & (num - 1);
    }

    int hammingWeight(int n)
    {
        int count = 0;

        while (n)
        {
            n = lowbit(n);
            count++;
        }

        return count;
    }
};

力扣136.只出现一次的数字

力扣136.只出现一次的数字

问题描述：

Quote

给你一个非空整数数组nums，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

你必须设计并实现线性时间复杂度的算法来解决此问题，且该算法只使用常量额外空间。

示例 1 ：

C++
1
2
输入：nums = [2,2,1]
输出：1

示例 2 ：

C++
1
2
输入：nums = [4,1,2,1,2]
输出：4

示例 3 ：

C++
1
2
输入：nums = [1]
输出：1

思路分析：

根据题意，只有一个元素出现一次，其他均出现两次，所以可以考虑使用位运算中的异或运算的a ^ a = 0、a ^ 0 = a和结合律三个性质，将数组所有的元素进行整体异或放到一个结果result中，结果中最后只会保留只出现一次的数字

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
class Solution136
{
public:
    int singleNumber(vector<int> &nums)
    {
        int ans = 0;
        // 使用异或运算的结合律和异或运算的性质
        for (auto num: nums)
        {
            ans ^= num;
        }

        return ans;
    }
};

力扣260.只出现一次的数字Ⅲ

力扣260.只出现一次的数字Ⅲ

问题描述：

Quote

给你一个整数数组nums，其中恰好有两个元素只出现一次，其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按任意顺序返回答案。

你必须设计并实现线性时间复杂度的算法且仅使用常量额外空间来解决此问题。

示例 1：

C++
1
2
3
输入：nums = [1,2,1,3,2,5]
输出：[3,5]
解释：[5, 3] 也是有效的答案。

示例 2：

C++
1
2
输入：nums = [-1,0]
输出：[-1,0]

示例 3：

C++
1
2
输入：nums = [0,1]
输出：[1,0]

思路分析：

本题是力扣136题的变体，本题中有两个只出现一次的数字，第一步还是一样，先通过异或运算取出只出现一次的两个数字的异或结果，但是接下来就需要该结果进行拆分，考虑取出两个数异或结果中最低位的1，之所以要这样做，是因为异或运算本质就是找不同，对于只出现一次两个数字来说，一定存在某一位是不同的，根据这一点就可以将原数组中的数字根据这一位是否相同拆分为两类，以数组[1,2,1,3,2,5]为例，示意图如下：

根据前面位运算的常见技巧，可以使用n&(-n)取出最右侧的1，根据这个1的位置就可以通过按位与取出与该位相同的数字和不同的数字，从而将原数组的数据分离为两组，因为存在两个只出现一次的数字，所以需要两个变量，对分类后的数字进行整体异或（利用异或运算的结合律）就可以实现将只出现一次的两个数字的异或结果进行拆分

需要注意，本题存在有符号整型溢出情况，考虑将异或结果存在一个无符号整型变量中

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution260_1
{
public:
    vector<int> singleNumber(vector<int> &nums)
    {
        size_t ans = 0;
        // 先获取到两个出现一次的数字
        for (auto n : nums)
        {
            ans ^= n;
        }

        // 根据结果ans对原数据进行分组
        vector<int> ret(2);
        // 取出最低位的1所在的位置
        int pos = ans & (-ans);
        // 分组
        for (int i = 0; i < nums.size(); i++)
        {
            if (nums[i] & pos)
            {
                ret[0] ^= nums[i];
            }
            else
            {
                ret[1] ^= nums[i];
            }
        }

        return ret;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution260_2
{
public:
    vector<int> singleNumber(vector<int> &nums)
    {
        size_t ans = 0;
        // 先获取到两个出现一次的数字
        for (auto n : nums)
        {
            ans ^= n;
        }

        // 根据结果ans对原数据进行分组
        vector<int> ret(2);
        // 取出最低位的1所在的位置
        int pos = ans & (-ans);
        // 分组
        for (auto n : nums)
        {
            ret[(n & pos) != 0] ^= n;
        }

        return ret;
    }
};

力扣268.丢失的数字

类似于力扣LCR173题：力扣268.丢失的数字

本题只考虑力扣LCR173题中的哈希表、等差数列和异或运算的思路

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution268_1
{
public:
    int missingNumber(vector<int> &nums)
    {
        // 数组哈希
        vector<int> hash(nums.size() + 1);
        for (auto n: nums)
        {
            hash[n]++;
        }

        int index = 0;
        for (int i = 0; i <= nums.size() + 1; i++)
        {
            if (!hash[i])
            {
                index = i;
                break;
            }
        }

        return index;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
class Solution268_2
{
public:
    int missingNumber(vector<int> &nums)
    {
        // 等差数列
        int sum = (0 + nums.size()) * (nums.size() + 1) / 2;

        return sum - accumulate(nums.begin(), nums.end(), 0);
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution268_3
{
public:
    int missingNumber(vector<int> &nums)
    {
        int xorSum = 0;
        // 异或运算结合律
        for (auto n: nums)
        {
            xorSum ^= n;
        }

        // 枚举长度个数字
        for (int i = 0; i <= nums.size(); i++)
        {
            xorSum ^= i;
        }

        return xorSum;
    }
};

力扣137.只出现一次的数字II

力扣137.只出现一次的数字II

问题描述：

Quote

给你一个整数数组nums，除某个元素仅出现一次外，其余每个元素都恰出现三次 。请你找出并返回那个只出现了一次的元素。

你必须设计并实现线性时间复杂度的算法且使用常数级空间来解决此问题。

示例 1：

C++
1
2
输入：nums = [2,2,3,2]
输出：3

示例 2：

C++
1
2
输入：nums = [0,1,0,1,0,1,99]
输出：99

思路分析：

  1. 解法1：排序+双指针

  2. 解法2：位运算

    对于「只出现一次的数字」系列的题目，基本都可以直接考虑使用位运算，本题也不例外，但是直接使用异或运算就会取出数组中所有不同的数字异或的结果，这样肯定是无法求出最后需要的只出现一次的数字。考虑下面的思路：

    只出现一次的数字也是一个单独的数字，其二进制表示肯定存在一定个数的1和0，而对于其他数字来说，因为其出现了3次，所以假如只考虑某一位二进制位，则数组中所有的数字中，出现三次的数字其该位二进制一定会出现3次，而只出现一次的数字其该位二进制不是0就是1，以数组[0,1,0,1,0,1,99]，所以就有下面的组合：

    因为整型为32位二进制位，则每一个二进制位都有上面的组合情况，那么上面的组合就变为了下面的情况：

    如果对上面的每一种组合的总和来说，其结果总会存在3的倍数，所以每一种组合都对3进行取余，最后就会剩下只出现一次的数字的二进制位，如下图所示：

    利用上面的思路就可以得出只出现一次的数字

关键步骤：

有了上面的思路，下面考虑如何编写代码。

首先因为整型有32为比特位，因为需要考虑每一位，所以需要一层循环控制当前二进制位

接着因为要获取某一位是1还是0，所以需要使用到(n>>i)&1，如果该表达式结果为真，则证明n当前位置为1，在图中表现就是4种情况，此时需要计算增加其中一种组合的总和用于代表某一个数字当前二进制位置是否为1，而因为要计算整个数组中所有的数值同一个二进制位的总和，所以需要循环遍历整个数组

上面的步骤结束后，此时sum中存储的就是其中一种情况下对应组合的总和，接下来进行对3取余的操作判断当前位是否为1，如果为1，证明该位一定是只出现一次的数字的对应二进制位，通过一个变量result，将该变量中对应的位置变为1

一直重复上面的步骤最后result中存储的就是只出现一次的数字

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution137_1
{
public:
    int singleNumber(vector<int> &nums)
    {
        int slow = 0;
        int fast = 0;
        sort(nums.begin(), nums.end());
        if (nums.size() == 1)
        {
            return nums[slow];
        }
        while (fast < nums.size())
        {
            if (nums[slow + 1] == nums[fast])
            {
                fast++;
            }
            else
            {
                slow = fast;
                fast++;
                if (fast < nums.size() && nums[fast] != nums[slow])
                {
                    break;
                }
            }
        }
        return nums[slow];
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution137_2
{
public:
    int singleNumber(vector<int> &nums)
    {
        int ret = 0;
        // 枚举32次依次填充ret使得ret中存储只出现一次的元素
        for (int i = 0; i < 32; i++)
        {
            // 计算每一位的和
            int sum = 0;
            for (auto n: nums)
            {
                if ((n >> i) & 1)
                {
                    sum++;
                }
            }

            // 取出只出现一次的元素的比特位
            sum %= 3;

            // 将ret对应的位置标记为sum的值
            // 如果sum为1，代表只出现一次的元素当前位为1
            if (sum)
            {
                ret |= (1 << i);
            }
        }

        // ret中存储的就是结果
        return ret;
    }
};

力扣面试题01.01.判定字符是否唯一

力扣面试题01.01.判定字符是否唯一

问题描述：

Quote

实现一个算法，确定一个字符串s的所有字符是否全都不同。

示例 1：

C++
1
2
输入: s = "leetcode"
输出: false

示例 2：

C++
1
2
输入: s = "abc"
输出: true

限制：

  • 0 <=len(s)<= 100
  • s[i]仅包含小写字母
  • 如果你不使用额外的数据结构，会很加分。

思路分析：

  1. 解法1：哈希表

  2. 解法2：位图思想

    因为字符只有26个，并且「是否唯一」可以转化为「是否已经存在」，如果已经存在，则说明该字符重复，否则不重复

优化思路：

根据鸽巢原理，因为小写字母一共26个，在不保证不重复的情况下，字符串s最多只有26个字符，如果大于26，则说明一定有重复

鸽巢原理

鸽巢原理：有n个鸽子巢，有n+1个鸽子，如果将鸽子放入鸽子巢中，那么至少会存在一个鸽子巢中的鸽子数量大于或等于1

参考资料：鸽巢原理

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution0101_1_1
{
public:
    bool isUnique(string astr)
    {
        int hash[128] = {0};
        // 统计个数
        for (auto ch: astr)
        {
            hash[ch]++;
        }

        // 判断是否存在某一个字符出现个数大于1
        for (auto num: hash)
        {
            if (num > 1)
            {
                return false;
            }
        }

        return true;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
class Solution0101_1_2
{
public:
    bool isUnique(string astr)
    {
        int hash[26] = {0};

        for (auto ch: astr)
        {
            // 如果已经存在，则说明一定出现重复
            if (hash[ch - 'a'] != 0)
            {
                return false;
            }
            hash[ch - 'a']++;
        }

        return true;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution0101_2_1
{
public:
    bool isUnique(string astr)
    {
        int ans = 0;

        // 位图思想
        for (auto ch: astr)
        {
            // 判断指定位置是否已经为1
            if ((ans >> ((int) (ch - 'a'))) & 1)
            {
                return false;
            }
            // 将指定位置置为1
            ans |= (1 << (int) (ch - 'a'));
        }

        return true;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution0101_2_2
{
public:
    bool isUnique(string astr)
    {
        // 使用鸽巢原理
        // 字符串长度大于26一定存在重复
        if (astr.size() > 26)
        {
            return false;
        }
        int ans = 0;

        // 位图思想
        for (auto ch: astr)
        {
            // 判断指定位置是否已经为1
            if ((ans >> ((int) (ch - 'a'))) & 1)
            {
                return false;
            }
            // 将指定位置置为1
            ans |= (1 << (int) (ch - 'a'));
        }

        return true;
    }
};

力扣371.两整数之和

力扣371.两整数之和

问题描述：

Quote

给你两个整数a和b，不使用运算符+和-​​​​​​​，计算并返回两整数之和。

示例 1：

C++
1
2
输入：a = 1, b = 2
输出：3

示例 2：

C++
1
2
输入：a = 2, b = 3
输出：5

思路分析：

  1. 解法1：直接加法（笔试时可用）

  2. 解法2：位运算

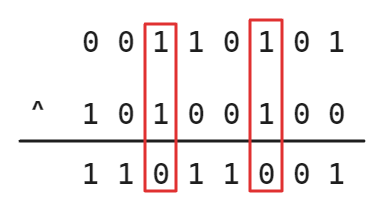
    本题位运算的思路利用到了异或运算的「无进位相加」性质，但是因为是无进位，所以还需要考虑进位问题。观察下面的示意图：

    可以看到只有同时出现1的时候才会进位，而进位的结果为1，那么就需要得到这个进位1，考虑使用按位与运算，因为按位与运算的性质是「有0则0，同时为1才为1」，所以刚好满足同时为1时结果为1，但是进位是向前进位，所以还需要将按位与运算的结果向左移动1位，示意图如下：

    获取到了进位和无进位结果，接下来就是将二者合并，合并过程本质还是一次加法，所以依旧需要使用异或运算。但是，这一次合并并不就是最后一次加法运算，因为进位和无进位异或可能还会存在一次进位过程，所以这整个过程就是一个循环，接下来就是判断何时结束循环，因为获取进位是通过按位与运算，如果进位和无进位按位与按位与刚好没有进位，则此时的进位就为0，所以可以通过进位是否为0来判断循环何时结束

参考代码：

C++
1
2
3
4
5
6
7
8
class Solution371_1
{
public:
    int getSum(int a, int b)
    {
        return a + b;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution371_2
{
public:
    int getSum(int a, int b)
    {
        // 异或运算：无进位相加
        int xorSum = a ^ b;
        // 获取进位
        // int carry = (a & b) << 1;
        // 防止移动负数左移未定义行为可以将原数值类型改为无符号
        size_t carry = size_t(a & b) << 1;
        while (carry)
        {
            a = xorSum;
            b = carry;
            xorSum = a ^ b;
            carry = size_t(a & b) << 1;
        }

        return xorSum;
    }
};

力扣面试题17.19.消失的两个数字

力扣面试题17.19.消失的两个数字

问题描述：

Quote

给定一个数组，包含从1到N所有的整数，但其中缺了两个数字。你能在O(N)时间内只用O(1)的空间找到它们吗？

以任意顺序返回这两个数字均可。

示例 1:

C++
1
2
输入: [1]
输出: [2,3]

示例 2:

C++
1
2
输入: [2,3]
输出: [1,4]

思路分析：

  1. 解法1：哈希表

  2. 解法2：位运算

    本题位运算可以考虑结合力扣268题和力扣260题的思路，具体如下：

    因为缺失两个数字，可以用力扣268题的思路，将数组中的数据和不缺失数字的数据进行整体异或放到结果result中，此时result中存储的就是缺失的两个数字异或的结果，再使用力扣260题的思路，将异或结果中的数据进行分组从而拆分出缺失的两个数字

关键步骤：

因为本题每个数字都只出现一次，所以在分组时如果仅使用数组中的数字进行整体异或依旧无法得出最后答案，所以分组时除了对数组中的数字进行整体异或外还需要对不缺失数字的集合再进行一次整体异或

如果觉得上面的步骤复杂，也可以考虑将不缺失数字的集合的数字依次插入到原数组，这样就可以直接将题目转化为力扣260题

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution17_19_1
{
public:
    vector<int> missingTwo(vector<int> &nums)
    {
        int sz = nums.size();
        vector<int> hash(sz + 3);
        vector<int> ret;

        for (auto n: nums)
        {
            hash[n]++;
        }

        // 注意不缺失数字的集合一共有sz+2个数字
        for (int i = 1; i < sz + 3; i++)
        {
            if (!hash[i])
            {
                ret.push_back(i);
            }
        }

        return ret;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class Solution17_19_2_1
{
public:
    vector<int> missingTwo(vector<int> &nums)
    {
        int sz = nums.size();
        int ans = 0;
        // 先获取到两个出现一次的数字
        for (auto n: nums)
        {
            ans ^= n;
        }
        for (int i = 1; i <= nums.size() + 2; i++)
        {
            ans ^= i;
        }

        // 根据结果ans对原数据进行分组
        vector<int> ret(2);
        // 取出最低位的1所在的位置
        // int pos = ans & (-ans);
        // 注意防止溢出
        int pos = (ans == INT_MIN) ? ans : ans & (-ans);
        // 分组
        for (int i = 0; i < nums.size(); i++)
        {
            if (nums[i] & pos)
            {
                ret[0] ^= nums[i];
            }
            else
            {
                ret[1] ^= nums[i];
            }
        }

        for (int i = 1; i <= nums.size() + 2; i++)
        {
            if (i & pos)
            {
                ret[0] ^= i;
            }
            else
            {
                ret[1] ^= i;
            }
        }

        return ret;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution17_19_2
{
public:
    vector<int> missingTwo(vector<int> &nums)
    {
        int sz = nums.size();
        int ans = 0;
        for (int i = 1; i <= sz + 2; i++)
        {
            nums.push_back(i);
        }
        // 先获取到两个出现一次的数字
        for (auto n: nums)
        {
            ans ^= n;
        }

        // 根据结果ans对原数据进行分组
        vector<int> ret(2);
        // 取出最低位的1所在的位置
        // int pos = ans & (-ans);
        // 注意防止溢出
        int pos = (ans == INT_MIN) ? ans : ans & (-ans);
        // 分组
        for (int i = 0; i < nums.size(); i++)
        {
            if (nums[i] & pos)
            {
                ret[0] ^= nums[i];
            }
            else
            {
                ret[1] ^= nums[i];
            }
        }

        return ret;
    }
};