栈和队列基础练习¶
约 5507 个字 1380 行代码 4 张图片 预计阅读时间 36 分钟
本篇介绍¶
栈和队列在其工作逻辑的特殊性可以让某些题目的解答更简单,下面是最基础或最典型的栈和队列的使用题目。本篇将根据这些题目加深对栈和队列的使用熟练度
力扣225.用队列实现栈¶
问题描述:
Quote
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和empty)。
实现MyStack类:
void push(int x)将元素 x 压入栈顶。 int pop()移除并返回栈顶元素。 int top()返回栈顶元素。 boolean empty()如果栈是空的,返回true;否则,返回false。
注意:
你只能使用队列的标准操作 —— 也就是push to back、peek/pop from front、size和is empty这些操作。 你所使用的语言也许不支持队列。你可以使用list(列表)或者deque(双端队列)来模拟一个队列,只要是标准的队列操作即可。
示例:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 | |
思路分析:
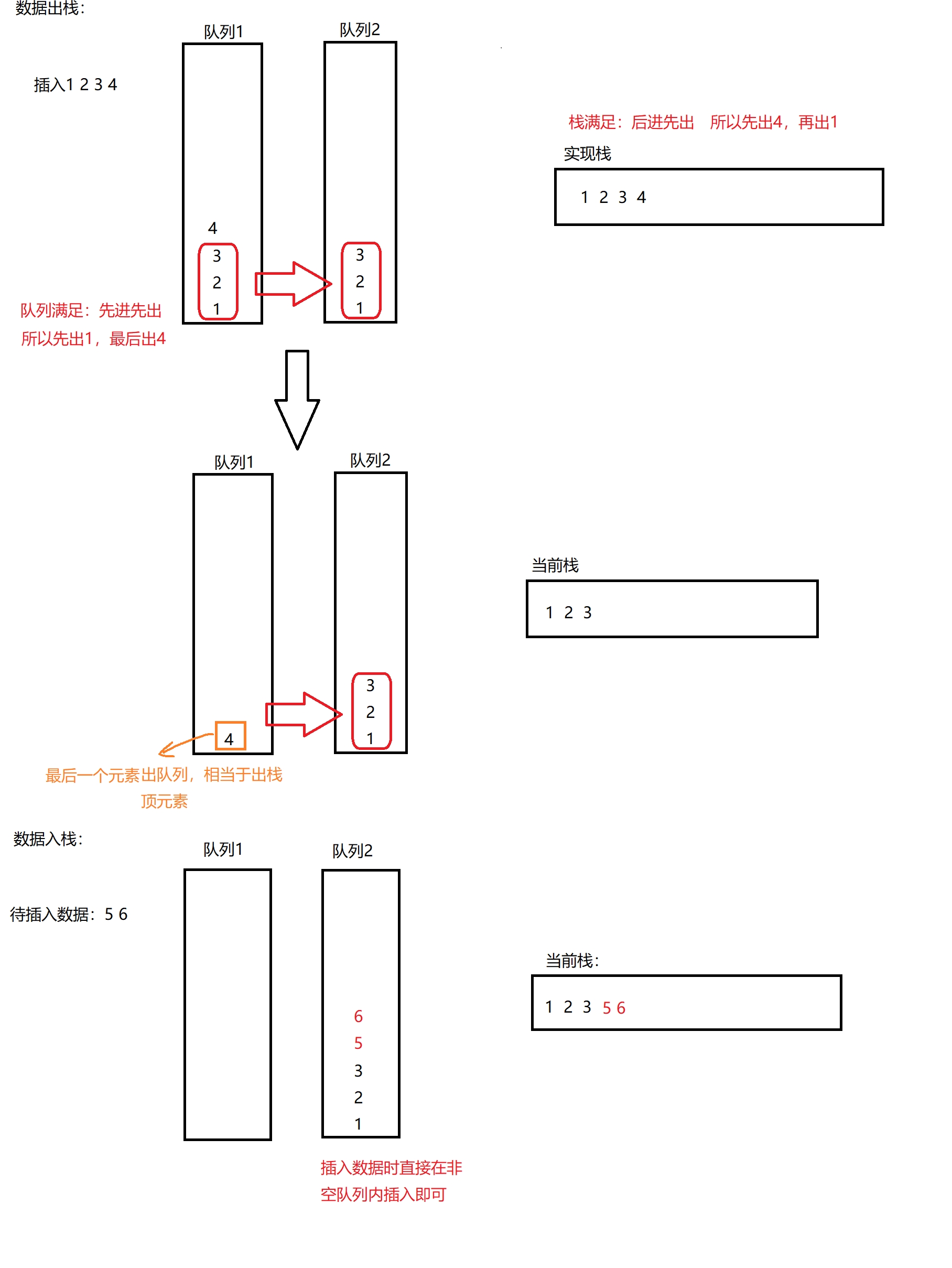
本题要求用两个队列实现一个栈,队列的入队和出队顺序为先进先出,而栈的入栈和出栈顺序为后进先出,则在设计时可以参考以下思路:
因为队列满足先进先出,所以一个队列中的数据转移到另一个队列时不改变原来队列中数据的排列顺序,但是栈的数据是后进先出,所以当非空队列向空队列转移数据时只需要保留非空队列中的最后一个数据,再让该数据出队即可,而栈和队列的添加数据顺序相同,都是放在最后一个数据后的位置,所以插入数据只需要插入到当前非空队列的尾部即可
思路优化:
本题也可以考虑使用一个队列实现栈,可以考虑:遍历过程中,将元素从尾部弹出,再从头部插入直到最后一个元素为止。因为需要确保队列中至少还有一个数,该数值代表的就是栈顶元素,所以还需要的一个变量用于统计当前队列的元素个数,当该变量值为1时就停止前面的操作,此时队头元素就是栈顶元素
参考代码:
| C | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 | |
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 | |
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 | |
力扣232.用栈实现队列¶
问题描述:
Quote
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):
实现MyQueue类:
void push(int x)将元素 x 推到队列的末尾 int pop()从队列的开头移除并返回元素 int peek()返回队列开头的元素 boolean empty()如果队列为空,返回true;否则,返回false 说明:
你只能使用标准的栈操作 —— 也就是只有push to top, peek/pop from top, size, 和is empty操作是合法的。 你所使用的语言也许不支持栈。你可以使用list或者deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。
示例 1:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 | |
思路分析:
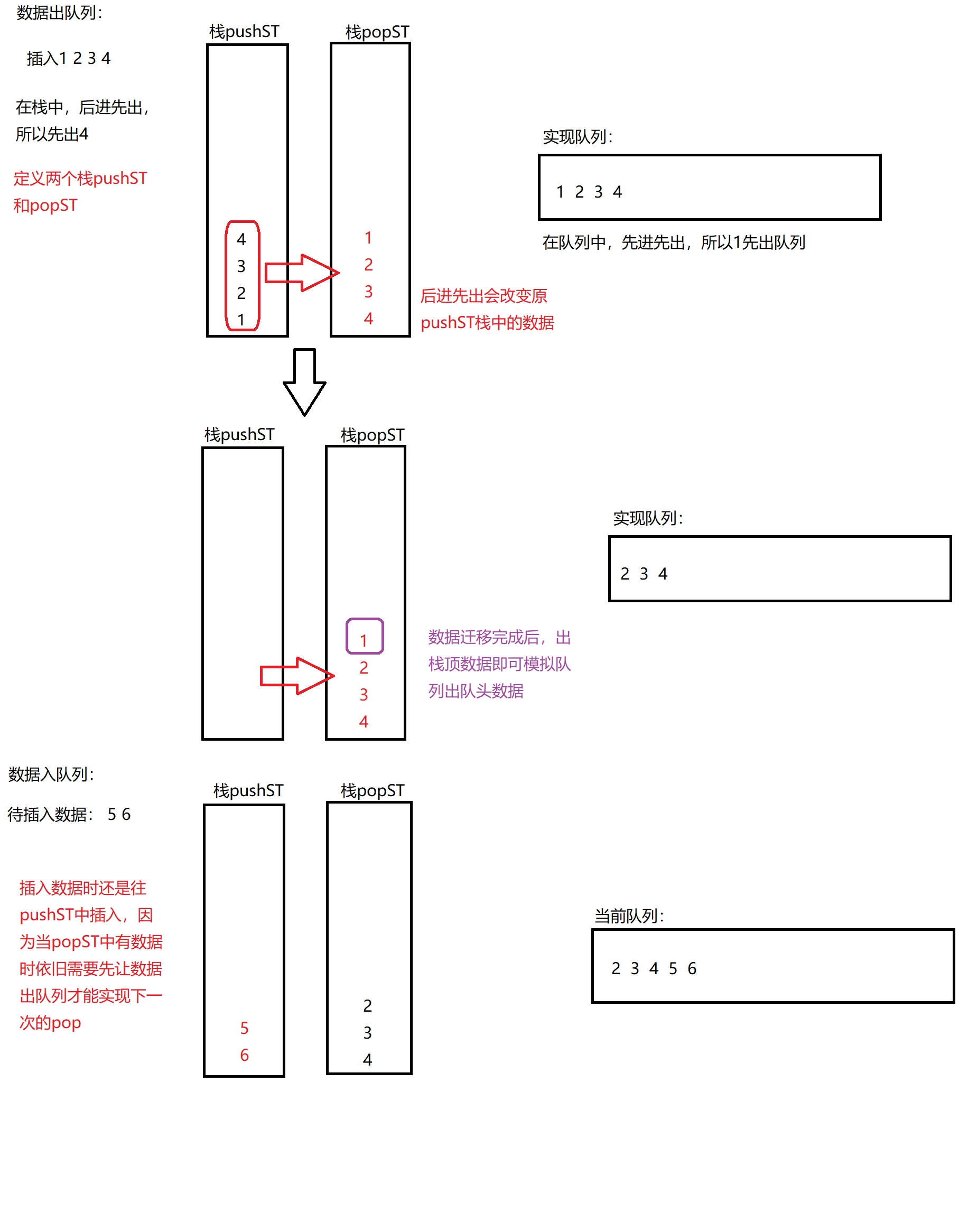
定义两个栈,但是不同于上题的两个队列(两个队列没有区分),本题中的两个栈需要作区分,一个栈作为数据出模拟队列的栈,称为pushSt,另一个作为数据入模拟队列的栈,称为popSt
因为数据出栈顺序为后进先出,所以在pushSt中的数据转移到popSt中后会改变原数据的顺序,而改变后的顺序中数据出栈刚好和队列中的数据出队相同,所以可以区分两个不同的栈,一个专用为存储进队列的数据,另一个专用为存储出队列的数据,当popSt数据全部出完后再将pushSt中数据转移到popSt进行下一次的数据出队
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 | |
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 | |
力扣622.设计循环队列¶
问题描述:
Quote
设计你的循环队列实现。循环队列是一种线性数据结构,其操作表现基于FIFO(先进先出)原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。
循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里,一旦一个队列满了,我们就不能插入下一个元素,即使在队列前面仍有空间。但是使用循环队列,我们能使用这些空间去存储新的值。
你的实现应该支持如下操作:
MyCircularQueue(k):构造器,设置队列长度为k。 Front:从队首获取元素。如果队列为空,返回-1。 Rear:获取队尾元素。如果队列为空,返回-1。 enQueue(value):向循环队列插入一个元素。如果成功插入则返回真。 deQueue():从循环队列中删除一个元素。如果成功删除则返回真。 isEmpty():检查循环队列是否为空。 isFull():检查循环队列是否已满。
示例:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 | |
思路分析:
-
C语言思路:
设计一个循环队列时需要考虑如何区分什么时候代表队列为满和队列为空,因为本题可以用数组来实现,故可以考虑当最后一个数据的位置的下一个位置为第一个元素所在的位置即为队列满状态,同样,可以定义一个记录有效数据的变量,当有效数据值为0时说明循环队列为空(注意不要使用该变量判断是否未满,因为数据在存储到数组中的最后一个有效位置时,还可以因为是循环回到数组的第一个有效位置开始继续存),下面是本题的每一个函数的基本思路:
-
循环队列的结构体设计
在循环队列中,需要有一个队列存在,故需要一个指向数组的指针
data,另外需要一个数据的位置的下一个位置,故需要一个变量rear记录该位置,而因为需要获取队头数据,故需要一个变量front记录该位置(切忌认为数组的第一个数据即为队头数据),再者需要一个变量记录当前队列中的有效数据个数size,最后因为题目并未固定循环队列的大小,故需要一个变量k来确定数组在开辟时的大小 -
循环队列的初始化
在循环队列的初始化函数
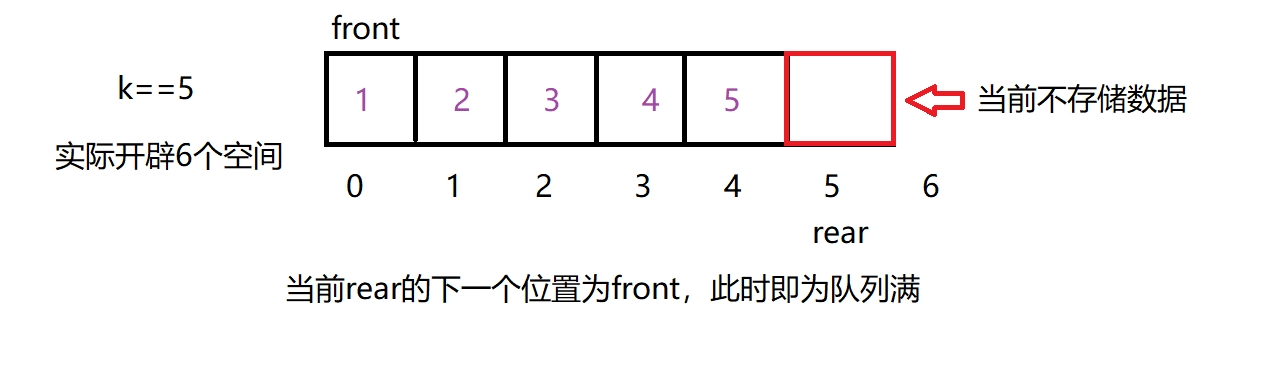
MyCircularQueue *myCircularQueueCreate(int k)中,函数参数为循环队列的大小,所以初始化过程中不可遗忘将该k给结构中的k,另外在初始化过程中,开辟的数组大小为k+1,但是数组的最后一个有效位置(即第k个位置)在队头指针front为数组的第一个元素的位置时不存储数据,其作用是在判断数组的下一个数据的位置时不会是因为循环回到了front的位置从而使rear == front因为数组本身的物理结构是不可循环的(即数组下标不会在下一次访问越界时直接回到开头位置,需要人为控制),所以本题的主要思路是通过求余运算结果来代替数组的下标,而因为当前数组的有效大小为
k+1,此时数组最后一个有效数据下一个位置的下标为k(也即当前的rear位置),那么构成循环队列就是让rear指针指向的下一个有效数据位置为数组第一个元素的位置,那么因为数组实际开辟了6个空间,最后一个位置的下标为5,则有规律:小于6的数值取6的模可以得到原来被除数(即余数),大于等于6的数值取6的模可以得到被除数大于6的部分(即余数),此时直接用rear当做被除数,而k+1为除数来使下标构成循环,从而达到循环队列的目的,特殊情况例如,当rear越界为6时取6的模可以直接回到数组的第一个元素的位置,即rear % (k+1) -
判断队列为空和判断队列为满
队列为空说明
size == 0(或者front == rear时(注意这个判断用在开辟的空间为k+1时)); 队列为满说明front == (rear + 1) % (k + 1),即当前rear所在位置的下一个位置 -
数据入队和数据出队
数据入队时,首先需要判断是否队列为满,如果队列为满直接返回
false,不为满时向rear % (k + 1)的位置添加数据,同时更新rear = (rear + 1) % (k + 1)和size;数据出队时,需要判断队列是否为空,如果队列为空则直接放回false,不为空才可以删除数据,队列删除数据时会改变头的位置,所以需要更新front,即front = (front + 1) % (k + 1),同时需要更新size -
获取队列头数据和获取队列尾数据
如果队列不为空,则队列头数据即为
front所在的位置的数据,否则无数据返回-1;如果队列不为空,则队列尾数据为rear所在位置的前一个位置的数据,但是注意rear为有效数据的下一个位置,所以需要获取rear的上一个位置的下标,参考取模思路,因为数组的最后一个元素下标为k,而模为k + 1,此时被除数取k + 1的模可以得到0 ~ k值,因为rear % (k + 1)可以取到的范围已经是0 ~ k,所以此时需要加最大模值使被除数增大才可以使模从0开始,而最大增加数为k,所以此时取(rear + k) % (k + 1)即可返回到rear上一个元素的位置 -
循环队列空间释放
释放空间需要先释放数组的空间,再释放循环队列结构的空间
-
-
C++思路:
所需成员:
- 使用
vector<int>作为循环队列的底层结构,在初始化时使用resize函数提前开辟k个空间。 front和back:因为需要找到队列的队尾元素和队头元素,所以使用front成员和back成员作为循环队列的两个属性分别指向队头元素和队尾元素maxLen:需要注意,因为vector<int>在空间不够时会进行扩容,但是在本题的循环队列中不能出现扩容的情况,所以考虑使用一个成员maxLen记录当前循环队列最多能存储的元素个数,就算出现扩容,只要元素个数大于maxLen都不允许插入。- 最后就是一个成员
num记录当前循环队列中的元素个数
总体思路:当
num == maxLen时代表当前循环队列已经插满,需要注意,初始状态下front和back也指向同一个位置,所以不可以仅仅判断front和back都指向同一个位置时循环队列已满- 插入元素时,先判断循环队列是否已满,接着判断
back是否已经到达最后一个元素的下一个位置,如果已经到达则需要使用取余进行修正,此时只需要使用back % maxLen即可,剩下的就是插入元素的逻辑 - 删除元素时,先判断循环队列是否为空,接着因为是数组,只需要移动
front即可。注意删除的元素有可能是当前数组的最后一个元素,此时向后front就导致front越界,按照循环队列的特点,此时front应该在数组第一个元素的位置 - 取出队头元素时,先判断循环队列是否为空。因为
front指向的就是当前元素,所以直接返回front对应的元素即可 - 取出队尾元素时,先判断循环队列是否为空。因为
back指向的是当前元素的下一个元素(但是除去第一个元素),所以对于第一个元素来说,直接取出back对应的元素即可,否则取出back - 1对应的元素 - 判断循环队列是否为空只需要判断有效数据个数
num是否为0即可,判断循环队列是否已满只需要判断有效数据个数是否满足num == maxLen即可
- 使用
Note
注意上面的两个思路都可以使用任何一个语言都可以实现,上面的分类只是思路对应的代码使用的语言不同而已
参考代码:
| C | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 | |
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 | |
力扣20.有效的括号¶
问题描述:
Quote
定一个只包括'(',')','{','}','[',']'的字符串s,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。 左括号必须以正确的顺序闭合。 每个右括号都有一个对应的相同类型的左括号。
示例 1:
| C++ | |
|---|---|
1 2 3 | |
示例 2:
| C++ | |
|---|---|
1 2 3 | |
示例 3:
| C++ | |
|---|---|
1 2 3 | |
示例 4:
| C++ | |
|---|---|
1 2 3 | |
思路分析:
本题可以使用栈来解决,当括号为左侧括号时,将括号存入栈内,当括号为右侧括号时,将该括号与栈顶的括号进行比较,比较一次进行一次出栈操作
错误思路:哈希表
本题不可以使用哈希表,所谓有效的括号是指左括号中指定括号的顺序必须和右括号中指定括号出现的顺序刚好匹配, 例如,左括号先为"([",那么此时右括号的顺序应该就是"])",而不是")]"。可以理解为右括号翻转后与左括号个数相同且刚好是回文串就属于有效括号,根据上面的理解,此时哈希表就不可以使用,因为哈希表主要是判断个数是否存在,但是不会考虑出现顺序
参考代码:
| C | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 | |
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 | |
力扣1047.删除字符串中的所有相邻重复项¶
问题描述:
Quote
给出由小写字母组成的字符串s,重复项删除操作会选择两个相邻且相同的字母,并删除它们。
在s上反复执行重复项删除操作,直到无法继续删除。
在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。
示例:
| C++ | |
|---|---|
1 2 3 4 | |
思路分析:
本题可以使用栈结构,遍历原字符串,依次向栈内插入字符,如果即将插入的字符与栈顶的字符相同,那么就不插入当前字符并且弹出当前栈顶的字符,一直持续到字符串遍历结束。最后栈内的字符就是结果,只需要逆序存储到原字符串中即可
代码优化:
因为C++中的string也支持push_back和pop_back,所以可以直接string模拟栈结构
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | |
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | |
力扣150.逆波兰表达式求值¶
力扣239.滑动窗口最大值¶
问题描述:
Quote
给你一个整数数组nums,有一个大小为k的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的k个数字。滑动窗口每次只向右移动一位。
返回滑动窗口中的最大值。
示例 1:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 | |
示例 2:
| C++ | |
|---|---|
1 2 | |
思路分析:
-
解法1:暴力解法
两次
for循环,第一层for循环遍历原数组,第二层for循环遍历对应的窗口找出最大值 -
解法2:单调队列
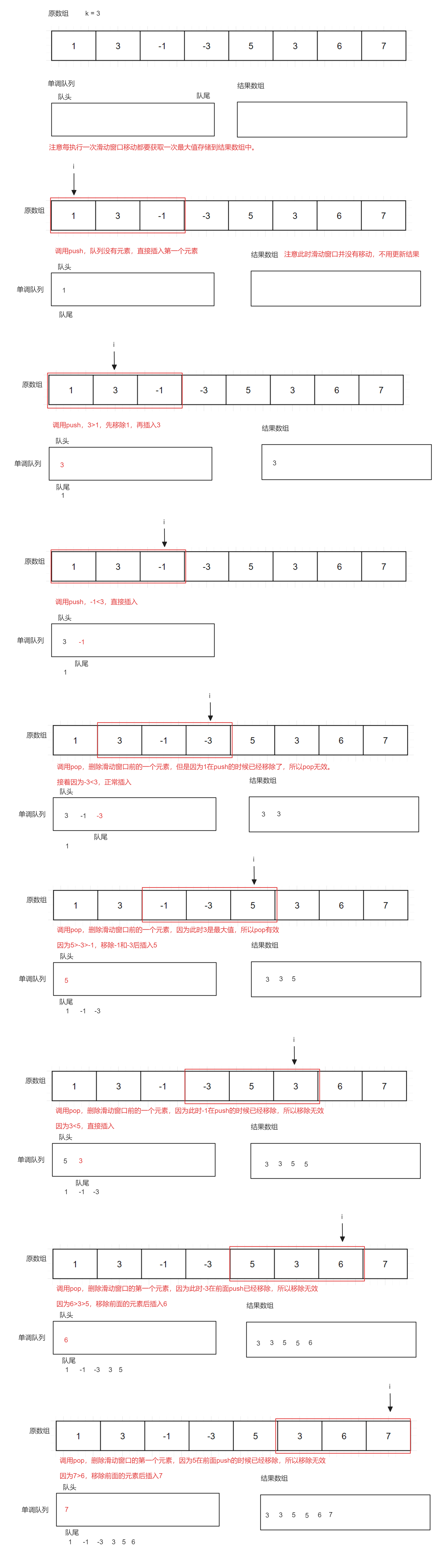
所谓单调队列,就是队列中的元素满足某一种单调性,一般为单调递增或者单调递减。单调队列也是一种队列,但是这个队列比较特殊,其队头和队列都会存在移除元素,所以不能直接使用queue作为底层结构。在C++中,支持队头插入元素和删除元素以及队尾插入元素和删除元素,并且高效的结构是deque,本次实现单调队列同样使用到deque而不是queue
在本题中,因为要找到滑动窗口中的最大值,所以可以考虑如果待插入的元素大于当前队头元素就移除队头元素一直到队头元素大于待插入的元素,此时队尾一定就是滑动窗口的最大值,这就是单调队列插入元素的思路。当下一个最大值要插入时,因为要保证一直从队尾中取到新的最大值,就需要在插入下一个最大值之前移除之前的最大值,这就是单调队列移除元素的思路。还可以实现一个函数表示获取到最大值,最大值就是队尾的元素,直接返回队尾元素即可
以示例1为例,下面是单调队列的执行过程:
在执行上面的过程中就可以看到单调队列中,从队尾开始到队头,单调队列的元素都是单调递减的,因为最大值在队尾
关键步骤:
本题使用单调队列一定要注意何时获取最大值,因为k至少为1,所以在i<=k时,滑动窗口一定不会移动,此时单独处理即可。后面的过程中,先弹出已有的元素,如果是最大值就会正常弹出,接着插入元素,因为插入元素会涉及到移除原来的最大值,所以下一步就可以获取一次最大值保证每一次获取最大值都在移动窗口之前
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 | |
力扣347.前K个高频元素¶
问题描述:
Quote
给你一个整数数组nums和一个整数k,请你返回其中出现频率前k高的元素。你可以按任意顺序返回答案。
示例 1:
| C++ | |
|---|---|
1 2 | |
示例 2:
| C++ | |
|---|---|
1 2 | |
思路分析:
-
解法1:map+排序:
使用map用于统计元素出现的次数,接着根据元素出现的次数进行排序,最后取出前k个即可
-
解法2:map+priority_queue
本题就是典型的TopK问题,可以直接使用堆解决,在C++中,优先级队列priority_queue底层就是堆结构。但是本题需要注意,堆中的比较基准是按照出现的频次,所以要单独实现一个比较仿函数
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 | |
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 | |
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 | |
力扣692.前K个高频单词¶
问题描述:
Quote
给定一个单词列表words和一个整数k,返回前k个出现次数最多的单词。
返回的答案应该按单词出现频率由高到低排序。如果不同的单词有相同出现频率,按字典顺序排序。
示例 1:
| C++ | |
|---|---|
1 2 3 4 | |
示例 2:
| C++ | |
|---|---|
1 2 3 4 | |
思路分析:
-
解法1:map+排序
思路和上一题基本一致,但是需要注意一个题目要求如果不同的单词有相同出现频率,按字典顺序排序,如果本题直接照搬前一题的思路,最后会出现一个问题:当出现相同出现频率的单词时,会因为
sort的不稳定性导致排序之后的出现相同出现频率的单词顺序发生了改变,在map插入统计的过程中其实已经按照了字典顺序排序,只是因为排序的不稳定导致,所以可以考虑两种方案:1. 使用稳定的排序函数stable_sort()2. 改变排序的逻辑:按照出现频率进行比较,出现频率大的排在前面,如果出现频率相同,则按照ASCII码进行比较排序 -
解法2:map+priority_queue
思路和上一题基本一致,但是需要注意一个题目要求如果不同的单词有相同出现频率,按字典顺序排序
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 | |
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 | |
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 | |
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 | |
力扣215.数组中的第K个最大元素¶
问题描述:
Quote
给定整数数组nums和整数k,请返回数组中第k个最大的元素。
请注意,你需要找的是数组排序后的第k个最大的元素,而不是第k个不同的元素。
你必须设计并实现时间复杂度为O(n)的算法解决此问题。
示例 1:
| C++ | |
|---|---|
1 2 | |
示例 2:
| C++ | |
|---|---|
1 2 | |
思路分析:
本题并不是单纯得获取到前K个最大元素,而是第前K个最大元素,还需要考虑如何取到第前K个。可以考虑使用数组元素个数减去k代表优先级队列需要弹出的元素,最后留下的堆顶元素就是第前K个最大元素
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | |