递归介绍¶

本篇介绍¶

在C语言函数部分已经简单介绍过递归。递归的本质就是函数自己调用自己，对于其概念和特点已经在该部分提及，本篇主要解决下面个问题：

1. 什么样的问题需要用递归
2. 学习递归的三个阶段
3. 如何写好一个递归
4. 循环与递归
5. 前序遍历和后序遍历

什么样的问题需要用递归¶

在前面的数据结构部分，一共遇到了三种用递归解决的问题，分别是：二叉树、快速排序和归并排序

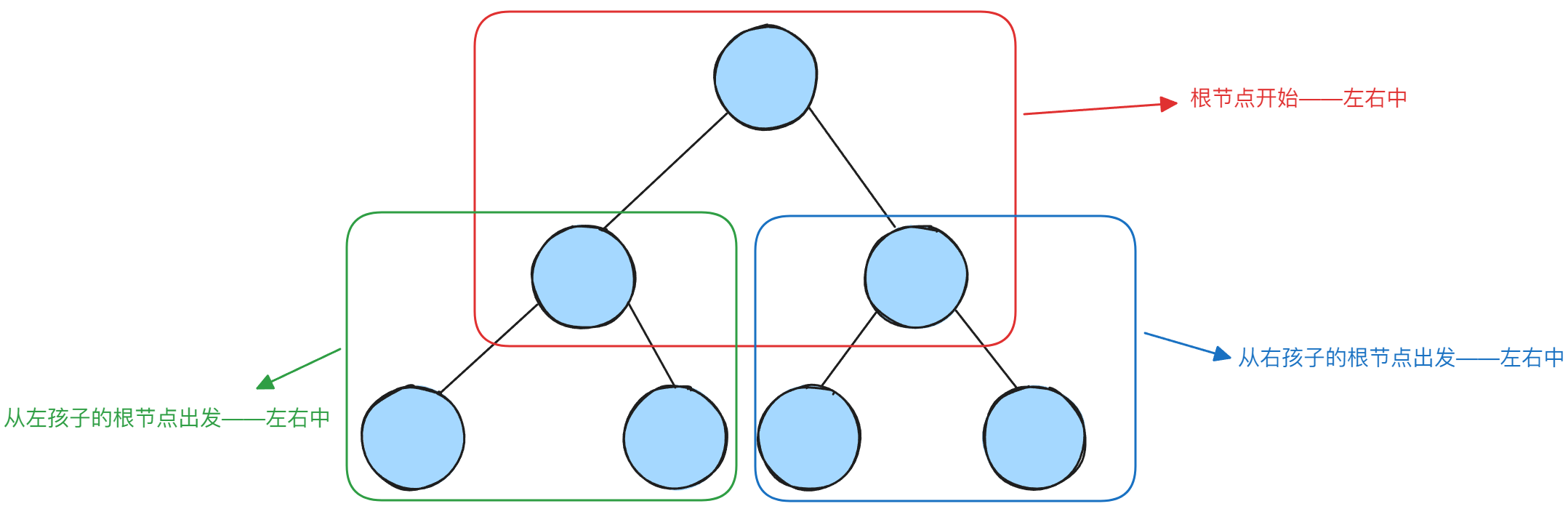
对于二叉树来说，以二叉树的后序遍历「左右中」为例，对于一棵普通的二叉树的根节点来说，就是先访问其左孩子节点，再访问其右孩子节点，最后访问根节点。在访问到根节点的左孩子节点或者右孩子节点时，也是接着按照前面同样的访问过程进行，示意图如下：

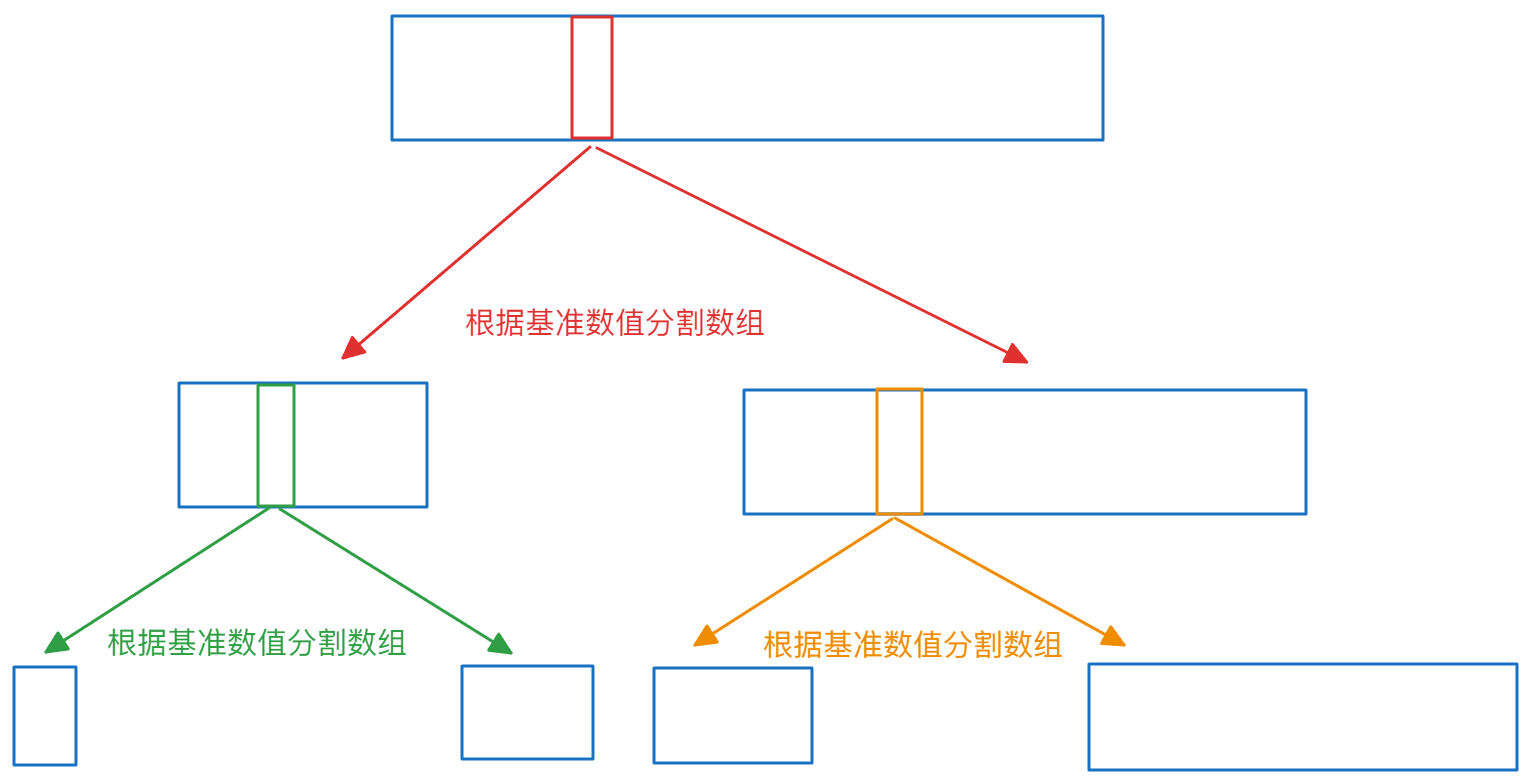
对于快速排序来说，需要对整个数组进行排序时，就根据一个基准数值，将数组分为两部分：一部分小于基准数值，另一部分大于基准数值，分为两部分后再进行排序，对于这两部分的排序过程来说又是选取一个基准数值继续同样的步骤，示意图如下：

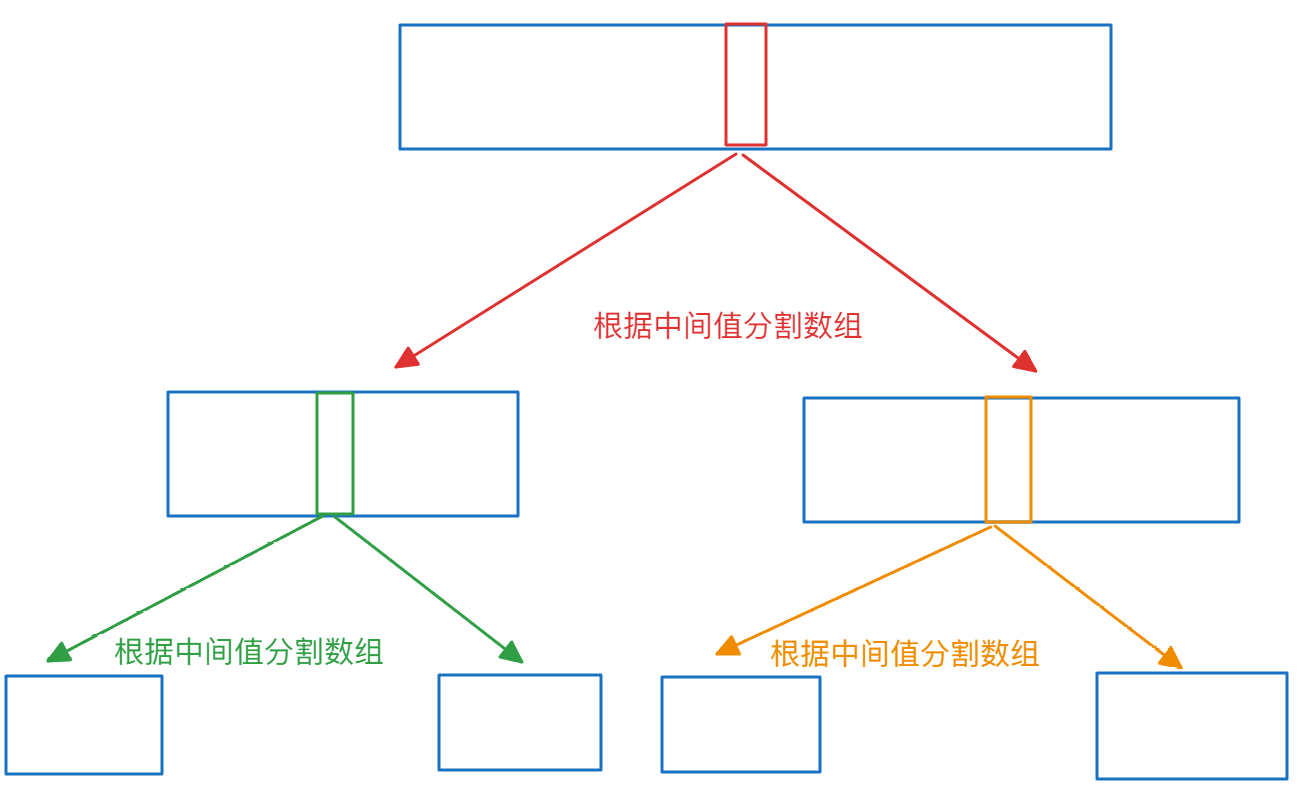
对于归并排序来说，其与快速排序非常类似，但是归并排序是直接选取中间节点作为切入点分割数组，对于分割后的两部分数组来说，其排序过程又是选取中间数值继续分割，示意图如下：

从上面三个例子可以看出，当主问题处理的逻辑和第二个子问题乃至第\(n\)个子问题的处理逻辑都是相同的情况下时就可以使用递归：

1. 对于二叉树后序遍历来说，根节点开始遍历的逻辑可以应用到其左孩子的遍历和右孩子的遍历
2. 对于快速排序和归并排序来说，主数组的切割逻辑可以应用到分割后的两个数组

学习递归的三个阶段¶

理解一个递归最直观的就是画递归展开图，在数据结构：二叉树（基础）部分已经提到过多次递归展开图，此处不再赘述。但是，递归展开图都有一个特点，那就是必须写完代码才能画递归展开图，所以在初学递归时可以使用递归展开图辅助理解递归，在接下来使用递归解题时，就必须想到在脱离根据代码画递归展开图时写出一个递归

通过递归展开图对递归的执行过程和特性有了一定的了解后，就进入了理解递归的第一个阶段，接下来就是以二叉树题目的辅佐完成从看懂递归到写出递归的转化，最后就是将递归应用于一些可以用递归解决的普通题目

当前已经完成了第一个阶段，现在准备迈进第二阶段，所以需要二叉树的大量练习，后面的题目先是关于二叉树的题目，再是关于递归在普通题目中的应用

如何写好一个递归¶

要写好一个递归，首先就必须知道递归的三要素：

1. 递归函数的参数和返回值设计：主问题和子问题都要用到的参数以及递归函数结束时需要向调用层返回的内容
2. 递归函数的终止条件：防止无限递归
3. 递归函数的单层逻辑：单个问题如何进行处理

以二叉树的后序遍历为例，根据上面的三要素写出二叉树的后序遍历代码：

首先分析二叉树后序遍历函数的参数，前面提到二叉树的后序遍历本质就是从一个根节点出发找到左孩子和右孩子，所以参数只需要一个节点的指针就可以了，而对于递归函数的返回值，对于二叉树后序遍历来说，如果只是为了查看节点的值，那么就不需要向调用层返回任何内容，因为这个过程已经被递归函数的单层逻辑给处理完了；接下来设计递归函数的终止条件，二叉树后序遍历何时结束最直观的答案就是没有节点时结束，而当一个节点为nullptr时就代表递归结束，所以如果当前节点为空节点，说明递归就可以结束了；最后考虑递归函数的单层逻辑，二叉树后序遍历的单层逻辑可以是任意逻辑，如果只是为了查看后序遍历的结果，那么就可以将直接打印这个节点的值作为递归函数的单层逻辑

根据上面的分析，假设一个二叉树节点的结构为TreeNode，就可以写出下面的代码：

1. 递归函数的参数设计：void postOrderTraversal(TreeNode* root)
2. 递归函数的终止条件：if(root == nullptr) return;
3. 递归函数的单层逻辑：std::cout << root->val << std::endl;

即：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

void postOrderTraversal(TreeNode* root)
{
    // 递归终止条件
    if(root == nullptr)
        return;

    // 遍历左节点
    postOrderTraversal(root->left);
    // 遍历右节点
    postOrderTraversal(root->right);

    // 单层处理逻辑
    std::cout << root->val << std::endl;
}

以一个实际的题目为例，假设需要后序遍历[1,2,3,4,5]这棵树，就可以考虑下面的分析过程：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

      1
   2     3
4     5

1->左->2->左->4->左->nullptr，返回到4的函数栈帧空间
             4->右->nullptr，返回到4的函数栈帧空间
            打印当前节点，返回到2的函数栈帧空间
       2->右->5->左->nullptr，返回到5的函数栈帧空间
             5->右->nullptr，返回到5的函数栈帧空间
            打印当前节点，返回到2的函数栈帧空间
       打印当前节点，返回到1的函数栈帧空间
1->右->3->左->nullptr，返回到3的函数栈帧空间
       3->右->nullptr，返回到3的函数栈帧空间
       打印当前节点，返回到1的函数栈帧空间
打印当前节点，结束函数

深度优先遍历/搜索与广度优先遍历/搜索¶

遍历可以理解为「经过」，搜索可以理解为「查看」，只有经过了某个位置才可以查看该位置的详细信息，所以遍历更强调行为，搜索更强调结果，但是要进行搜索就必须进行遍历，所以一般二者是同时出现的，即搜索包括遍历

所谓深度优先遍历/搜索（Depth First Search，简称DFS）就是递归式得获取到每一个节点，其中涉及到栈、递归和回溯

所谓广度优先遍历/搜索（Breadth First Search，简称BFS）就是从一层的角度出发获取到每一个节点，其中涉及到队列

实际上，深度优先遍历/搜索和广度优先遍历/搜索都是搜索（或者暴搜）的分支，本质都是枚举到每一个节点

上面的两种方式如果对应于一棵二叉树，那么就有：

1. 深度优先遍历/搜索：前序遍历、中序遍历和后序遍历
2. 广度优先遍历/搜索：层序遍历

在解决全排列问题时，如果需要枚举每一种情况，在数学中可以使用树状图的形式解决，此处也称为这种树为决策树，对于这种树来说，其枚举方式也是通过深度优先搜索和广度优先搜索

循环与递归¶

所谓循环，就是重复执行某一段逻辑，这与递归的解决思路大体是一致的，所以循环的代码也可以转换为递归，同理，递归的代码也可以转化为循环。但是，并不是所有的循环代码转换为递归都比较高效和容易，也并不是所有的递归转换为循环都比较方便，一般情况下，当递归转向循环时，如果涉及到使用数据结构辅助才能做到，那么此时的循环就不是很占优势了，同理可得递归

此时代入一下二叉树的遍历，在二叉树的遍历过程中，除了一条路走到黑的情况外，还有可能存在分支，但是何处有分支并不能确定，所以还需要根据当前节点判断是否存在左孩子或者右孩子，如果是递归，那么在返回时就可以接着回到上一层调用位置判断该位置是否有分支，因为递归向下走肯定是要返回的，但是循环不同，执行了就是执行了，一旦执行就代表当前这一次的逻辑全部执行完毕，所以要使用循环实现二叉树的遍历就必须借助栈

但是对于数组的遍历，假设数组为nums，如果使用循环，代码如下：

1
2
3
4

for(int i = 0; i < nums.size(); i++)
{
    cout << nums[i] << " ";
}

而之所以可以这样写循环，本质就是因为数组是单分支的，即可以一条路走到黑，那么对于这种情况，使用递归也可以解决：

1
2
3
4
5
6
7
8

void dfs(vector<int>& nums, int i)
{
    if(nums.size() == i)
        return;

    cout << nums[i] << " ";
    dfs(nums, i + 1);
}

可以看到，只要当前逻辑能一次性处理完毕，那么递归和循环的代码都会比较简单易懂

前序遍历和后序遍历¶

此处就会引申出一个问题：使用递归倒序遍历数组，实际上只需要更改代码逻辑即可，既然是倒着遍历，那么就需要让函数先找到最后一个节点，在寻找的过程中不进行处理，直到最后一个节点的时候再开始处理就行了，所以代码可以写为：

1
2
3
4
5
6
7
8

void dfs(vector<int>& nums, int i)
{
    if(nums.size() == i)
        return;

    dfs(nums, i + 1);
    cout << nums[i] << " ";
}

从上面遍历数组的两个递归代码可以看出，前序遍历和后序遍历的本质区别就是处理目标的时机不同，在二叉树中也会提到：处理中间节点的时机不同，但是这里不会讨论中序遍历，因为中序遍历只适用于二叉树，对于多叉树以及单叉链，实际上只有前序遍历和后序遍历