跳转至

二叉树遍历相关题目

约 2628 个字 570 行代码 16 张图片 预计阅读时间 16 分钟

本篇介绍

二叉树主要考察的还是根据具体的遍历方式实现问题，所以在完成后面的题目之前先熟悉二叉树的遍历方式是非常重要的，与数据结构：二叉树（基础）篇不同，本次除了会包含递归解法外，还会包含迭代法

二叉树的遍历主要分为深度优先搜索和广度优先搜索，深度优先一般就是前中后序三个遍历方式，深度优先就是层序遍历，在下面的题目中，也主要考察这两种遍历方式

二叉树的深度优先搜索

力扣144.二叉树的前序遍历

力扣144.二叉树的前序遍历

问题描述：

Quote

给你二叉树的根节点root，返回它节点值的前序遍历。

示例 1：

C++
1
2
输入：root = [1,null,2,3]
输出：[1,2,3]

解释：

示例 2：

C++
1
2
输入：root = [1,2,3,4,5,null,8,null,null,6,7,9]
输出：[1,2,4,5,6,7,3,8,9]

解释：

示例 3：

C++
1
2
输入：root = []
输出：[]

示例 4：

C++
1
2
输入：root = [1]
输出：[1]

思路分析：

  1. 解法1：递归

    二叉树的前序遍历在数据结构：二叉树（基础）部分已经提过基本的递归思路，本题最简单的思路也就是递归写法，此处不再赘述

  2. 解法2：迭代

    二叉树前序遍历的迭代写法的主要思路就是用栈模拟递归的过程，因为前序遍历的顺序是：中左右，所以根节点是第一个被处理的节点，此时栈内的数据就是当前子树的根节点。如果栈不为空说明还没有走完整棵二叉树，否则每一次遍历时，先取出当前栈顶的元素，该元素就是当前子树的根节点，取出后弹出当前元素，接着走向右子树，注意不是左子树，因为栈是先进后出，而下一次是左子树先被去除，所以右子树先进才能保证左子树在栈顶

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution144_1
{
public:
    void _preorderTraversal(TreeNode *root, vector<int> &ret)
    {
        if (root == nullptr)
            return;

        // 处理节点
        ret.push_back(root->val);
        _preorderTraversal(root->left, ret);
        _preorderTraversal(root->right, ret);
    }

    vector<int> preorderTraversal(TreeNode *root)
    {
        vector<int> ret;
        _preorderTraversal(root, ret);
        return ret;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution144_2
{
public:
    vector<int> preorderTraversal(TreeNode *root)
    {
        // 用栈模拟
        stack<TreeNode *> st;
        // 先插入根节点
        st.push(root);
        vector<int> ret;

        while (!st.empty())
        {
            // 获取栈顶节点
            TreeNode *cur = st.top();
            st.pop();
            // 处理逻辑
            if (cur != nullptr)
                ret.push_back(cur->val);
            else
                continue;

            // 先插入右节点
            st.push(cur->right);
            // 再插入左节点
            st.push(cur->left);
        }

        return ret;
    }
};

力扣94.二叉树的中序遍历

力扣94.二叉树的中序遍历

问题描述：

Quote

给定一个二叉树的根节点root，返回它的中序遍历。

示例 1：

C++
1
2
输入：root = [1,null,2,3]
输出：[1,3,2]

示例 2：

C++
1
2
输入：root = []
输出：[]

示例 3：

C++
1
2
输入：root = [1]
输出：[1]

思路分析：

  1. 解法1：递归

    二叉树的中序遍历在数据结构：二叉树（基础）部分已经提过基本的递归思路，本题最简单的思路也就是递归写法，此处不再赘述

  2. 解法2：迭代

    二叉树中序遍历的迭代写法相对比较简单，先找到左子树，再取出当前节点，当取出左节点后，下一个节点一定是根节点，所以只需要将root更新为nullptr就可以防止重复走到原来的节点。考虑到如果左节点是叶子，那么此时root->right一定为nullptr，所以可以更新为root = root->right，如果存在右节点，则下一次又会走右侧子树重复前面的步骤。如果不存在右节点，则下一次取出的就是根节点

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution94_1
{
public:
    void _inorderTraversal(TreeNode *cur, vector<int> &ret)
    {
        if (cur == nullptr)
            return;

        _inorderTraversal(cur->left, ret);
        ret.push_back(cur->val);
        _inorderTraversal(cur->right, ret);
    }

    vector<int> inorderTraversal(TreeNode *root)
    {
        vector<int> ret;
        _inorderTraversal(root, ret);

        return ret;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution94_2
{
public:
    vector<int> inorderTraversal(TreeNode *root)
    {
        stack<TreeNode *> st;
        vector<int> ret;

        TreeNode *prev = nullptr;

        while (!st.empty() || root != nullptr)
        {
            // 先找到最左节点
            while (root)
            {
                st.push(root);
                root = root->left;
            }

            // 获取当前节点
            root = st.top();
            st.pop();
            ret.push_back(root->val);

            // 不论是否为空都要走右子树，一旦右为空，下一次就会取到当前子树的根节点
            root = root->right;
        }

        return ret;
    }
};

力扣145.二叉树的后序遍历

力扣145.二叉树的后序遍历

问题描述：

Quote

给你一棵二叉树的根节点root，返回其节点值的后序遍历。

示例 1：

C++
1
2
3
输入：root = [1,null,2,3]

输出：[3,2,1]

解释：

示例 2：

C++
1
2
3
输入：root = [1,2,3,4,5,null,8,null,null,6,7,9]

输出：[4,6,7,5,2,9,8,3,1]

解释：

示例 3：

C++
1
2
3
输入：root = []

输出：[]

示例 4：

C++
1
2
3
输入：root = [1]

输出：[1]

思路分析：

  1. 解法1：递归

    二叉树的后序遍历在数据结构：二叉树（基础）部分已经提过基本的递归思路，本题最简单的思路也就是递归写法，此处不再赘述

  2. 解法2：迭代

    二叉树后序遍历的迭代写法有两种，一种是变向的前序遍历，另外一种就是常规意义上的后序遍历

    对于变向的前序遍历，其实就是根据后序遍历的顺序「中右左」的前序遍历的反向「左右中」，所以只需要将前序遍历的「中左右」改为「中右左」，再反向结果集即可。但是注意，这个方法只是完成了遍历的结果，遍历的方法基本上是不太严谨的，或者说是异构的前序遍历（即利用了两次反转：先反转为中右左，再反转结果集）

    常规意义上的后序遍历就是按照「左右中」的顺序进行，基本思路和中序遍历很类似，先一直走左子树，直到找到最左节点，这个过程中也要记录遍历过的节点。接着获取到当前节点，与中序不同的是，此时需要判断是否存在右孩子，因为后序遍历处理中间节点的逻辑是在遍历完右子树之后，如果右子树存在，那么还需要继续遍历，即将右子树节点压栈，否则当前节点就是当前子树的最后一个节点

关键步骤：

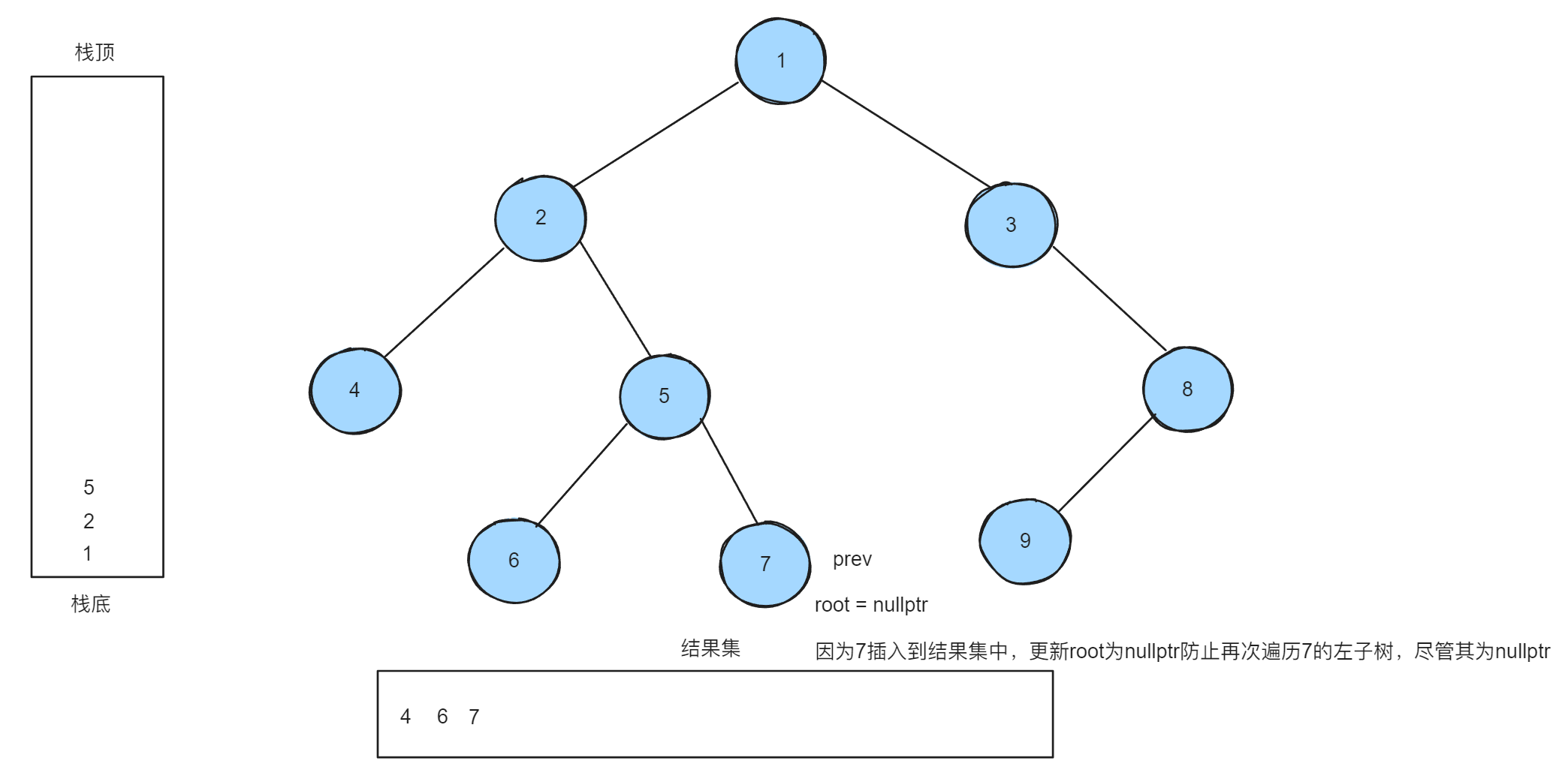
后序遍历的常规迭代法需要注意，要使用到一个变量prev表示前一个节点，如果当前节点的右孩子等于prev，说明当前子树的右子树遍历完毕，当前及诶点就是当前子树的根节点，并且还需要在插入节点到结果集之后将root置为空，防止多次走向同一棵左子树

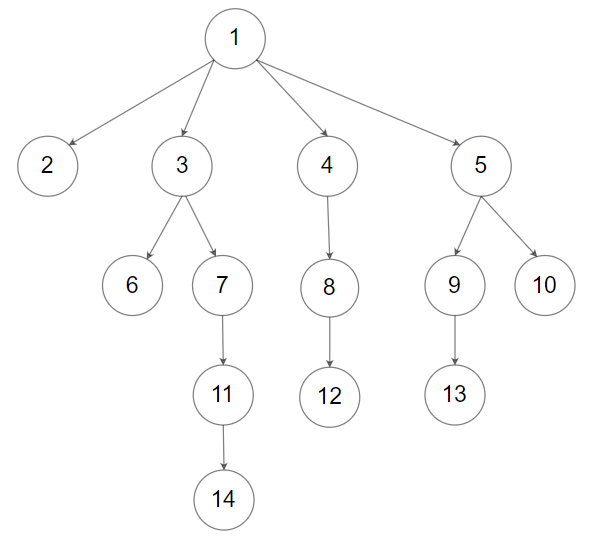
例如下面的例子中，prev当前指向的是7节点：

下一次循环中，首先会从栈内取出元素，当前栈顶元素为5，所以当前节点就是5，如果没有判断5的右子树是否等于prev，那么就会出现再一次走到右子树将5再次插入到栈内并再次走向同一棵右子树的情况

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution145_1
{
public:
    void _postOrderTraversal(TreeNode *cur, vector<int> &ret)
    {
        if (cur == nullptr)
            return;

        // 访问左节点
        _postOrderTraversal(cur->left, ret);
        // 访问右节点
        _postOrderTraversal(cur->right, ret);
        // 处理当前节点
        ret.push_back(cur->val);
    }

    vector<int> postorderTraversal(TreeNode *root)
    {
        vector<int> ret;
        _postOrderTraversal(root, ret);

        return ret;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class Solution145_2_1
{
public:
    vector<int> postorderTraversal(TreeNode *root)
    {
        vector<int> ret;
        // 使用栈模拟
        stack<TreeNode *> st;
        // 根节点为空直接返回空
        if (root == nullptr)
            return ret;

        // 防止满二叉子树死循环
        TreeNode *prev = nullptr;
        while (!st.empty() || root != nullptr)
        {
            // 一直找到最左节点
            while (root)
            {
                // 在循环中已经插入一次根节点
                // 此时循环上的判断root!=nullptr可以防止两个相同的根节点同时插入栈中
                st.push(root);
                root = root->left;
            }

            // 获取到当前节点
            root = st.top();
            st.pop();

            // 如果当前节点不存在右子树
            // 或者已经获取过同一个右子树
            // 说明已经遍历完成，当前节点就是子树根节点
            if (root->right == nullptr || root->right == prev)
            {
                ret.push_back(root->val);
                prev = root;
                // 将root置为空防止再一次获取最左节点
                root = nullptr;
            }
            else
            {
                // 存在右子树就还需要继续找
                st.push(root); // 将弹出的根节点再插入到栈中
                // 此时肯定不存在或者已经判断完左子树，所以直接走向右子树
                root = root->right;
            }
        }

        return ret;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution145_2_2
{
public:
    vector<int> postorderTraversal(TreeNode *root)
    {
        // 用栈模拟
        stack<TreeNode *> st;
        // 先插入根节点
        st.push(root);
        vector<int> ret;

        while (!st.empty())
        {
            // 获取栈顶节点
            TreeNode *cur = st.top();
            st.pop();
            // 处理逻辑
            if (cur != nullptr)
                ret.push_back(cur->val);
            else
                continue;

            // 中右左
            // 先插入左节点
            st.push(cur->left);
            // 再插入右节点
            st.push(cur->right);
        }

        reverse(ret.begin(), ret.end());

        return ret;
    }
};

二叉树的广度优先搜索

力扣102.二叉树的层序遍历

力扣102.二叉树的层序遍历

问题描述：

Quote

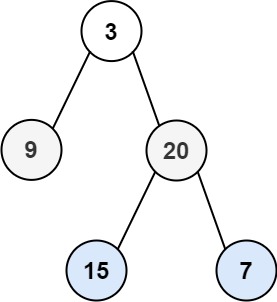
给你二叉树的根节点root，返回其节点值的层序遍历。（即逐层地，从左到右访问所有节点）。

示例 1：

C++
1
2
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

示例 2：

C++
1
2
输入：root = [1]
输出：[[1]]

示例 3：

C++
1
2
输入：root = []
输出：[]

思路分析：

二叉树的层序遍历就是利用队列，基本思路已经在数据结构：二叉树（基础）中提及，此处不再赘述，但是本题除了实现层序遍历二叉树外，还需要确定每一个节点所在的层，此时就需要使用到计数器，计数器由队列的大小进行初始化，起始是计数器为1，代表第一层只有一个节点，以此类推

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution102
{
public:
    vector<vector<int>> levelOrder(TreeNode *root)
    {
        // 记录当前层节点的个数
        int count = 0;
        vector<vector<int>> ret;

        queue<TreeNode *> que;

        que.push(root);
        while (!que.empty() && root != nullptr)
        {
            // 确定当前层节点的个数
            count = que.size();
            // 存储当前层的节点
            vector<int> temp;

            while (count--)
            {
                TreeNode *cur = que.front();
                que.pop();
                temp.push_back(cur->val);

                if (cur->left)
                    que.push(cur->left);
                if (cur->right)
                    que.push(cur->right);
            }

            ret.push_back(temp);
        }

        return ret;
    }
};

根据上面的层序遍历，可以完成下面类似的题目：

Info

下面的题目是部分与层序遍历相关的题目，后面也会有其他题目会使用到层序遍历的思路，代码也可能基本类似

力扣107.二叉树的层序遍历Ⅱ

力扣107.二叉树的层序遍历Ⅱ

问题描述：

Quote

给你二叉树的根节点root，返回其节点值自底向上的层序遍历。（即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）

示例 1：

C++
1
2
输入：root = [3,9,20,null,null,15,7]
输出：[[15,7],[9,20],[3]]

示例 2：

C++
1
2
输入：root = [1]
输出：[[1]]

示例 3：

C++
1
2
输入：root = []
输出：[]

思路分析：

本题就是将正常层序遍历的结果集反转即可

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution107
{
public:
    vector<vector<int>> levelOrderBottom(TreeNode *root)
    {
        // 记录当前层节点的个数
        int count = 0;
        vector<vector<int>> ret;

        queue<TreeNode *> que;

        que.push(root);
        while (!que.empty() && root != nullptr)
        {
            count = que.size();
            // 存储当前层的节点
            vector<int> temp;

            while (count--)
            {
                TreeNode *cur = que.front();
                que.pop();
                temp.push_back(cur->val);

                if (cur->left)
                    que.push(cur->left);
                if (cur->right)
                    que.push(cur->right);
            }

            ret.push_back(temp);
        }

        reverse(ret.begin(), ret.end());

        return ret;
    }
};

力扣199.二叉树的右视图

力扣199.二叉树的右视图

问题描述：

Quote

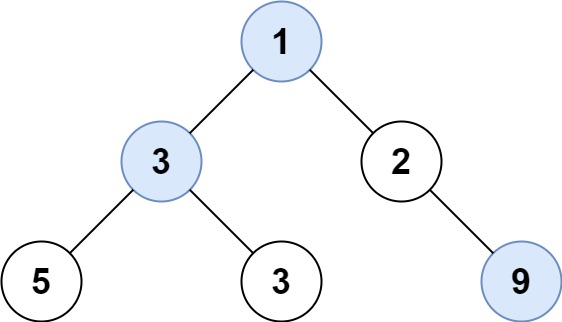
给定一个二叉树的根节点root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值

示例 1：

C++
1
2
输入：root = [1,2,3,null,5,null,4]
输出：[1,3,4]

解释：

示例 2：

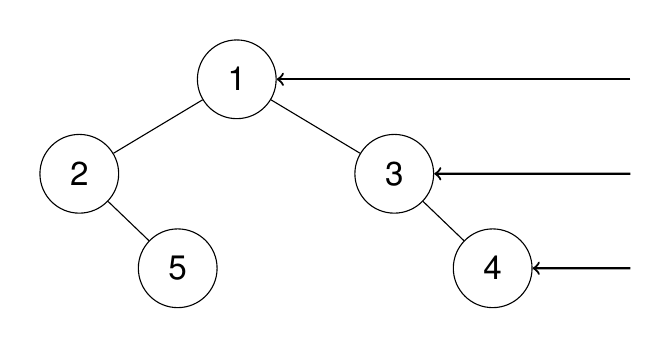
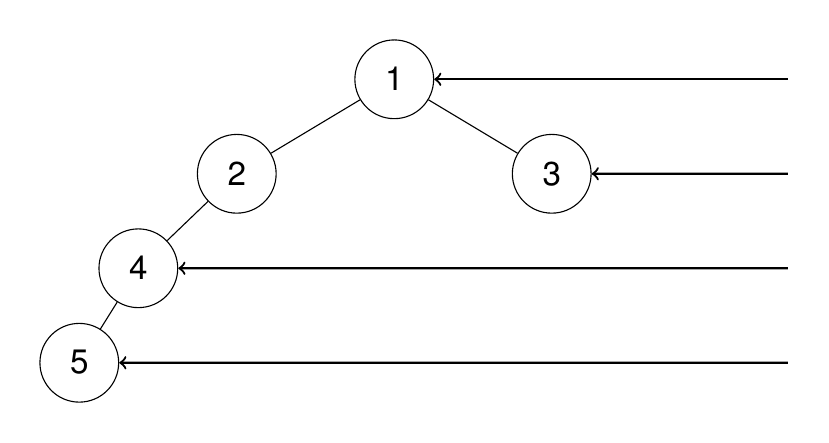
输入：root = [1,2,3,4,null,null,null,5]

输出：[1,3,4,5]

解释：

示例 3：

C++
1
2
输入：root = [1,null,3]
输出：[1,3]

示例 4：

C++
1
2
输入：root = []
输出：[]

思路分析：

所谓右视图，就是只看得到最右侧的节点，所以从层序遍历的角度来看，只需要取出每一层的最后一个节点即可

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution199
{
public:
    vector<int> rightSideView(TreeNode *root)
    {
        int count = 0;
        vector<int> ret;

        queue<TreeNode *> que;
        que.push(root);

        while (!que.empty() && root != nullptr)
        {
            count = que.size();
            while (count)
            {
                TreeNode *cur = que.front();
                que.pop();
                count--;
                // 当前层最后一个节点就是右视图可以看到的唯一节点
                if (count == 0)
                    ret.push_back(cur->val);

                if (cur->left)
                    que.push(cur->left);
                if (cur->right)
                    que.push(cur->right);
            }
        }

        return ret;
    }
};

力扣637.二叉树的层平均值

力扣637.二叉树的层平均值

问题描述：

Quote

给定一个非空二叉树的根节点root, 以数组的形式返回每一层节点的平均值。与实际答案相差\(10^{-5}\)以内的答案可以被接受。

示例 1：

C++
1
2
3
4
输入：root = [3,9,20,null,null,15,7]
输出：[3.00000,14.50000,11.00000]
解释：第 0 层的平均值为 3,第 1 层的平均值为 14.5,第 2 层的平均值为 11 。
因此返回 [3, 14.5, 11] 。

示例 2:

C++
1
2
输入：root = [3,9,20,15,7]
输出：[3.00000,14.50000,11.00000]

思路分析：

只需要在层序遍历中计算总和，最后在进入下一层之前计算当前层的平均值即可

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution637
{
public:
    vector<double> averageOfLevels(TreeNode *root)
    {
        // 记录每一层的总和
        double sum = 0;
        // 记录每一层节点的个数
        int count = 0;

        vector<double> ret;
        queue<TreeNode *> que;

        que.push(root);

        while (!que.empty())
        {
            count = que.size();
            int temp = count;
            while (temp--)
            {
                TreeNode *cur = que.front();
                que.pop();

                sum += cur->val;

                if (cur->left)
                    que.push(cur->left);
                if (cur->right)
                    que.push(cur->right);
            }

            // 计算平均值
            ret.push_back(sum / count);

            sum = 0;
        }

        return ret;
    }
};

力扣429.N叉树的层序遍历

力扣429.N叉树的层序遍历

问题描述：

Quote

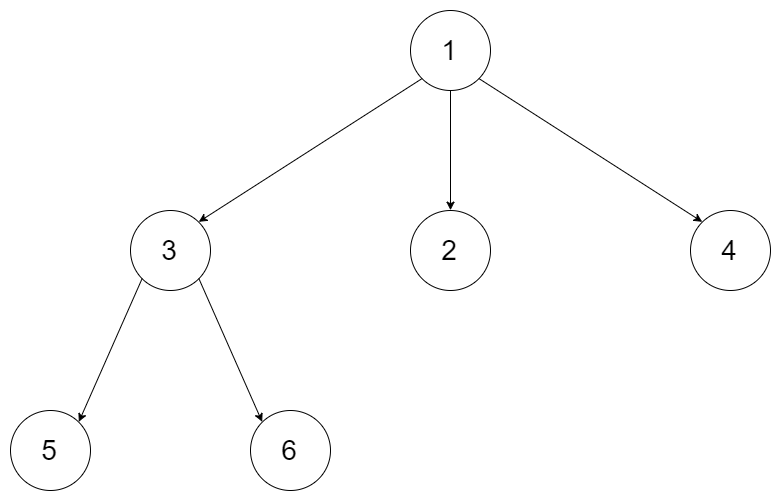
给定一个N叉树，返回其节点值的层序遍历。（即从左到右，逐层遍历）。

树的序列化输入是用层序遍历，每组子节点都由null值分隔（参见示例）。

示例 1：

C++
1
2
输入：root = [1,null,3,2,4,null,5,6]
输出：[[1],[3,2,4],[5,6]]

示例 2：

C++
1
2
输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：[[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]

思路分析：

基本思路还是层序遍历，但是注意，每一个孩子都存储在vector中，所以需要遍历vector将节点插入到队列

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution429
{
public:
    vector<vector<int>> levelOrder(Node* root)
    {
        int count = 0;

        vector<vector<int>> ret;
        queue<Node*> que;
        que.push(root);

        while(!que.empty() && root != nullptr)
        {
            count = que.size();
            vector<int> temp;
            while(count--)
            {
                Node* cur = que.front();
                que.pop();

                temp.push_back(cur->val);
                for(auto node : cur->children)
                    que.push(node);
            }

            ret.push_back(temp);
        }

        return ret;
    }
};

力扣515.在每个树行中找最大值

力扣515.在每个树行中找最大值

问题描述：

Quote

给定一棵二叉树的根节点root，请找出该二叉树中每一层的最大值。

示例1：

C++
1
2
输入: root = [1,3,2,5,3,null,9]
输出: [1,3,9]

示例2：

C++
1
2
输入: root = [1,2,3]
输出: [1,3]

思路分析：

使用层序遍历，在每一层中找出最大值即可

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution515
{
public:
    vector<int> largestValues(TreeNode* root)
    {
        int count = 0;

        vector<int> ret;

        queue<TreeNode*> que;
        que.push(root);

        while(!que.empty() && root != nullptr)
        {
            count = que.size();

            // 本题存在负数，初始值不可以为0
            // 否则当前层全是负数情况下无法找到最大值
            int maxVal = INT_MIN;
            while(count--)
            {
                TreeNode* cur = que.front();
                que.pop();

                maxVal = max(maxVal, cur->val);

                if(cur->left)
                    que.push(cur->left);

                if(cur->right)
                    que.push(cur->right);
            }
            ret.push_back(maxVal);
        }

        return ret;
    }
};

力扣116.填充每个节点的下一个右侧节点指针

力扣116.填充每个节点的下一个右侧节点指针

问题描述：

Quote

给定一个完美二叉树，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

C++
1
2
3
4
5
6
struct Node {
    int val;
    Node *left;
    Node *right;
    Node *next;
}

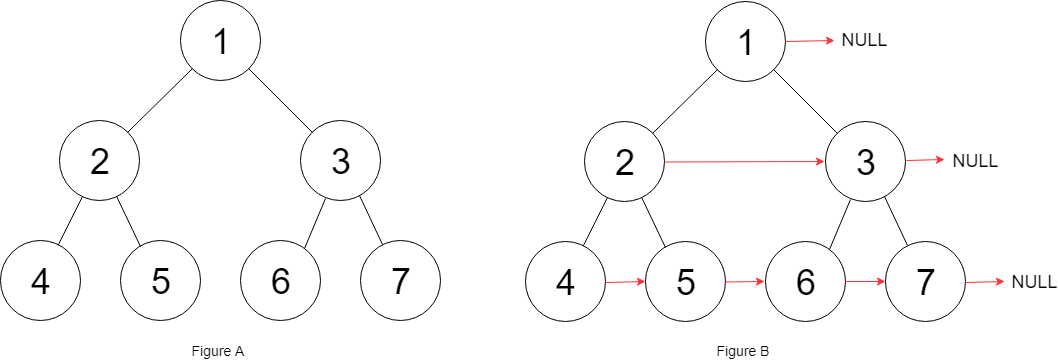
填充它的每个next指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将next指针设置为NULL。

初始状态下，所有next指针都被设置为NULL。

示例 1：

C++
1
2
3
输入：root = [1,2,3,4,5,6,7]
输出：[1,#,2,3,#,4,5,6,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化的输出按层序遍历排列，同一层节点由 next 指针连接，'#' 标志着每一层的结束。

示例 2:

C++
1
2
输入：root = []
输出：[]

思路分析：

使用层序遍历，将每一层的节点直接相连，除了每一层的最后一个节点需要指向空

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution116
{
public:
    Node *connect(Node *root)
    {
        int count = 0;

        queue<Node *> que;

        que.push(root);

        while (!que.empty() && root != nullptr)
        {
            count = que.size();

            while (count)
            {
                count--;
                Node *cur = que.front();
                que.pop();
                if (count == 0)
                    cur->next = nullptr;
                else
                    cur->next = que.front();

                if (cur->left)
                    que.push(cur->left);
                if (cur->right)
                    que.push(cur->right);
            }
        }

        return root;
    }
};

力扣117.填充每个节点的下一个右侧节点指针Ⅱ

类似力扣116.力扣117填充每个节点的下一个右侧节点指针Ⅱ

本题和116题不一样的是，本题是普通的二叉树，但是使用层序遍历不需要考虑这个问题，所以可以直接使用116题的代码：

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution117
{
public:
    Node *connect(Node *root)
    {
        int count = 0;

        queue<Node *> que;

        que.push(root);

        while (!que.empty() && root != nullptr)
        {
            count = que.size();

            while (count)
            {
                count--;
                Node *cur = que.front();
                que.pop();
                if (count == 0)
                    cur->next = nullptr;
                else
                    cur->next = que.front();

                if (cur->left)
                    que.push(cur->left);
                if (cur->right)
                    que.push(cur->right);
            }
        }

        return root;
    }
};