常规题目中的递归¶

本篇介绍¶

为了更好得理解应用递归，除了需要熟悉二叉树中使用递归外，还需要在一些普通的题目中能发现重复的子问题从而尝试应用递归解决，接下来的题目都是可以用迭代解决的题目，但是同样可以使用递归，做题的步骤应该从发现重复的子问题开始逐步思考如何用递归

力扣面试题08.06.汉诺塔问题¶

力扣面试题08.06.汉诺塔问题

问题描述：

1
2

输入：A = [2, 1, 0], B = [], C = []
输出：C = [2, 1, 0]

1
2

输入：A = [1, 0], B = [], C = []
输出：C = [1, 0]

思路分析：

本题的基本思路就是先结合移动限制模拟移动过程，找出移动中的规律，具体过程如下：

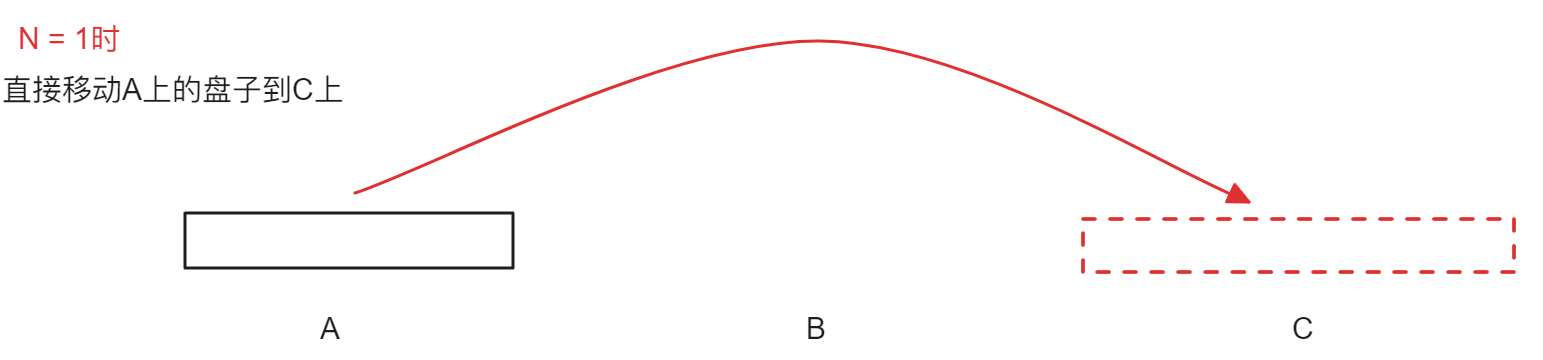
当N等于1时，考虑直接将A上的盘子移动到C上：

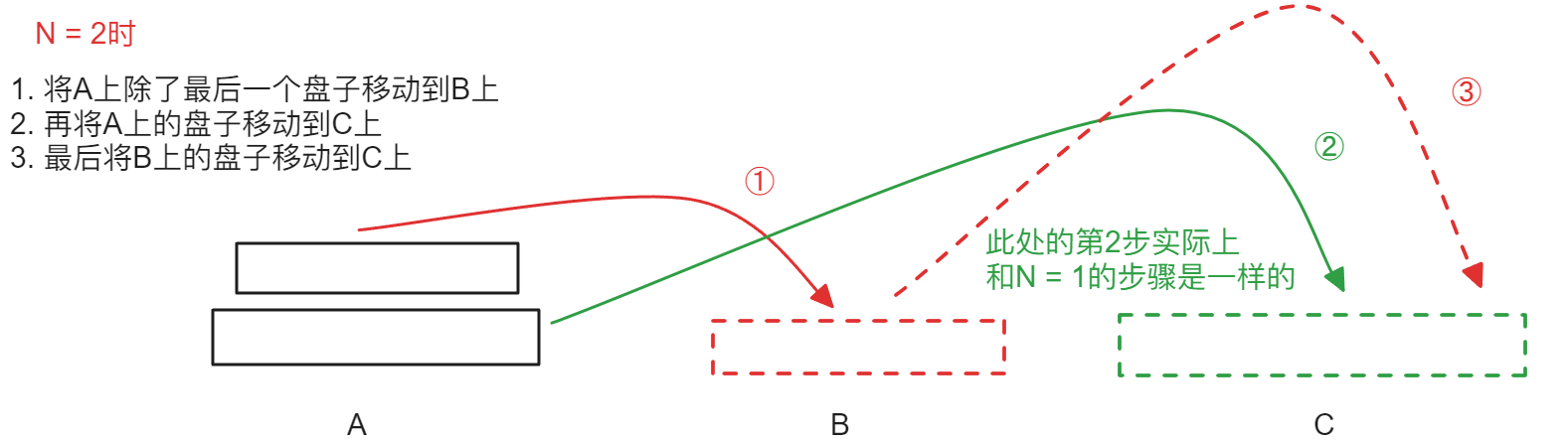
当N等于2时，先将A上除了最后一个盘子外的盘子移动到B上，再将A上的盘子移动到C上，最后将B上的盘子移动到C上

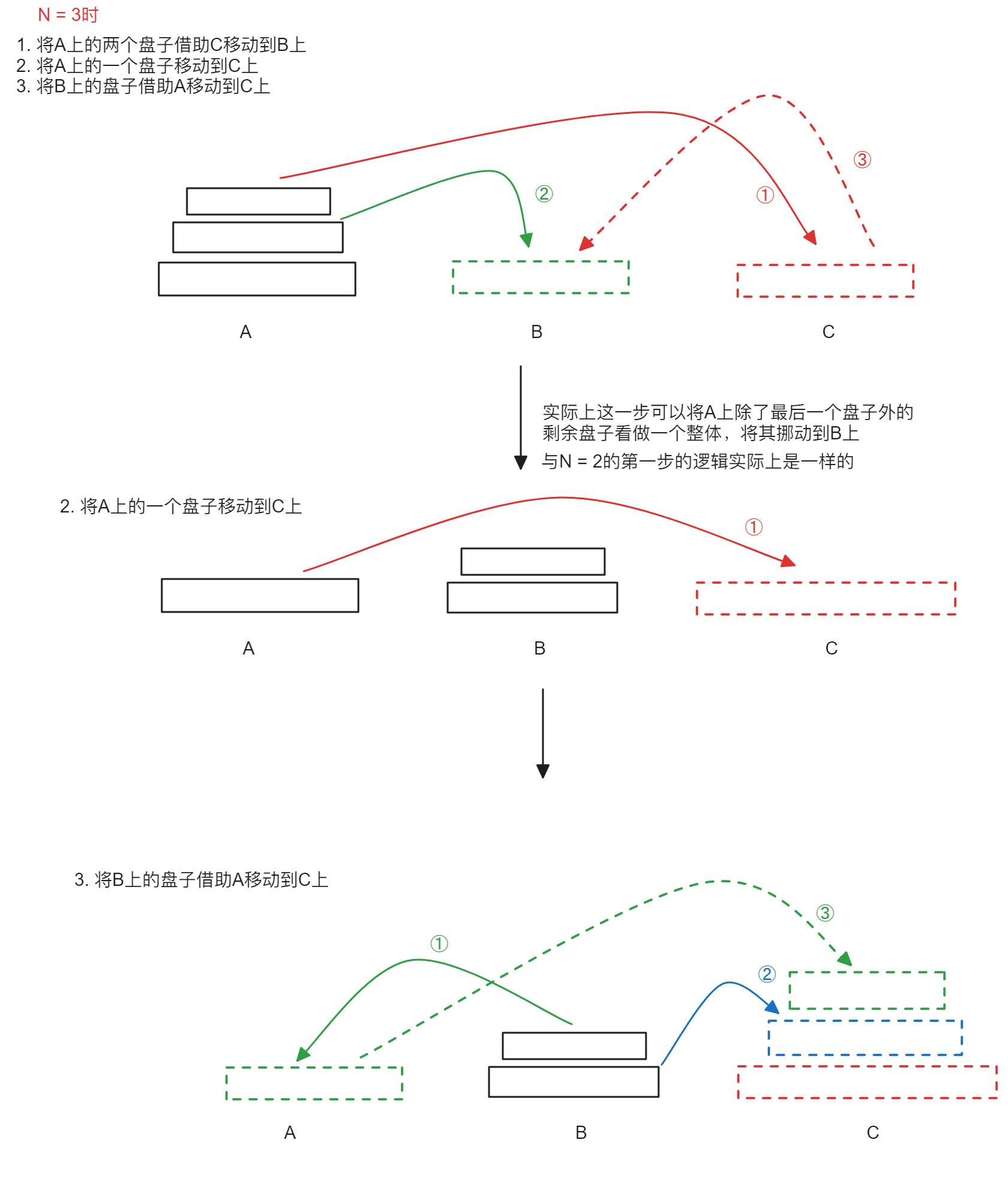
当N等于3时，先将A上除了最后一个盘子外的盘子移动到B上，再将A上的盘子移动到C上，最后将B上的盘子移动到C上

从上面的过程中可以看到，当N大于1时，除了最大的盘子以外，A上的盘子都需要通过一定的方式先移动到B，再移动A的最后一个盘子到C，再将B的盘子全部移动到C就完成了全部移动，那么在N=3时，移动A上除了最大的盘子以外的盘子到B的过程就相当于N=2的第一步，移动A上的最后一个盘子到C相当于N=2的第二步，将B上的盘子全部移动到C实际上就是相当于N=2的第三步，此时因为不止一个盘子所以借助了A，而N=2时只有一个盘子可以不需要借助A，N=2的第二步相当于N=1的第一步

根据上面的分析，如果N无穷大，那么始终都是三步：

1. 将A上除了最后一个盘子的其他盘子借助C移动到B上
2. 将A的最后一个盘子移动到C上
3. 将B上的盘子借助A移动到C上

所以可以推出递归三大要素：

1. 递归的函数头：本题的重复子问题就是根据N借助柱子移动盘子，但是要先移动A中盘子个数-1个盘子到B上，所以除了三个柱子以外，还需要一个计数器表示当前盘子个数
2. 递归的函数体：上面的三个步骤
3. 递归的结束条件：因为N=1时可以直接将A的盘子移动到C上，所以N=1时结束递归

笔试投机取巧

如果是笔试场景，面试官不知道代码，所以可以直接使用C = A结束问题

参考代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

class Solution0806_1
{
public:
    void _hanota(vector<int> &A, vector<int> &B, vector<int> &C, int num)
    {
        // 注意使用num而不是A.size()，因为要移动的是剩余盘子，A的元素个数不能直观反映还有多个盘子
        // 另一方面，使用num可以表示当前递归的层次，防止栈溢出的问题
        if (num == 1)
        {
            C.push_back(A.back());
            // 注意弹出最后一个元素
            A.pop_back();
            return;
        }

        _hanota(A, C, B, num - 1);
        C.push_back(A.back());
        // 注意弹出最后一个元素
        A.pop_back();
        _hanota(B, A, C, num - 1);
    }

    void hanota(vector<int> &A, vector<int> &B, vector<int> &C)
    {
        _hanota(A, B, C, A.size());
    }
};

1
2
3
4
5
6
7
8

class Solution0806_2
{
public:
    void hanota(vector<int> &A, vector<int> &B, vector<int> &C)
    {
        C = A;
    }
};

力扣21.合并两个有序链表¶

力扣21.合并两个有序链表

问题描述：

1
2

输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

1
2

输入：l1 = [], l2 = []
输出：[]

1
2

输入：l1 = [], l2 = [0]
输出：[0]

思路分析：

1. 解法1：迭代

   见算法：链表基础练习篇

2. 解法2：递归

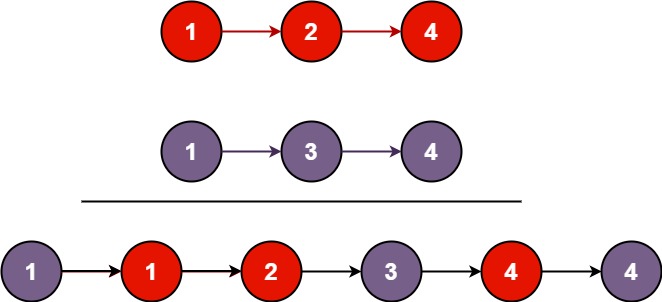
   除了根据迭代转换的递归解法外，还可以直接从本题切入找出重复子问题写出递归，而不需要通过循环过渡。可以先从主问题入手，主问题是合并链表，而合并的本质就是在两个链表中找到较大的尾插，即将较小的节点作为前驱节点，那么此时较小节点所在的链表剩余节点构成的链表和另外一个链表的合并就构成了和主问题相同的一个子问题

   找到重复的子问题后就可以设计函数头：因为合并链表需要用到两个链表的头，所以参数需要两个链表的头指针，并且函数需要返回一个头结点，接着设计函数体：将较小的作为链表头，本质就是将较小节点的next指向下一个较大的节点，所以分为两种情况：

   1. list1较小，向后移动list1，将此时的list1和list2再重复合并操作，合并完成后返回较小的节点作为新链表的头结点
   2. list2较小，向后移动list2，将此时的list1和list2再重复合并操作，合并完成后返回较小的节点作为新链表的头结点

参考代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

class Solution21
{
public:
    ListNode *mergeTwoLists(ListNode *list1, ListNode *list2)
    {
        // 递归出口——其中一个走到空就返回另外一个链接到结尾
        if (!list1)
            return list2;
        else if (!list2)
            return list1;

        // 较小的作为前驱节点链接
        if (list1->val <= list2->val)
        {
            list1->next = mergeTwoLists(list1->next, list2);
            return list1;
        }
        else if (list1->val > list2->val)
        {
            list2->next = mergeTwoLists(list1, list2->next);
            return list2;
        }

        // 不可达的return，但是为了防止编译器报错
        return nullptr;
    }
};

力扣206.反转链表¶

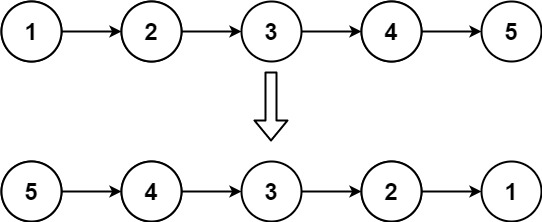
力扣206.反转链表

问题描述：

1
2

输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]

1
2

输入：head = [1,2]
输出：[2,1]

1
2

输入：head = []
输出：[]

思路分析：

1. 解法1：迭代

   见算法：链表基础练习篇

2. 解法2：递归

   除了算法：链表基础练习篇中提到的根据循环转换为递归解决外，可以考虑直接从题目出发找重复子问题写递归，此次递归的思路与之前根据循环转递归的思路不同，本次递归的思路：要直接反转第一个节点和第二个节点，就会丢失第三个节点，考虑先翻转后面的节点，翻转后面的节点的思路与翻转第一个和第二个是相同的，所以就是重复的子问题。考虑将链表看做一棵单叉树，使用后序遍历找到最后一个节点，如果当前节点的下一个节点为空时，说明是最后一个节点，将这个节点返回作为新链表的头结点，再翻转当前节点（倒数第二个节点）和当前节点的下一个节点（最后一个节点），注意翻转完成后将当前节点的next置为空，这个是统一处理，因为翻转后的链表的最后一个节点的next需要指向空，最后继续向上返回反转后的链表的头结点

参考代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

class Solution206
{
public:
    ListNode *reverseList(ListNode *head)
    {
        if (!head || !head->next)
            return head;

        ListNode *newHead = reverseList(head->next);
        head->next->next = head;
        head->next = nullptr;

        return newHead;
    }
};

力扣24.两两交换链表中的节点¶

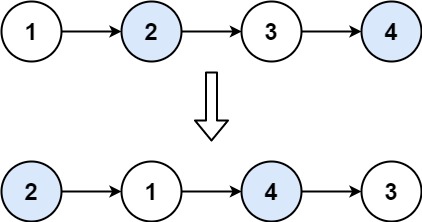
力扣24.两两交换链表中的节点

问题描述：

1
2

输入：head = [1,2,3,4]
输出：[2,1,4,3]

1
2

输入：head = []
输出：[]

1
2

输入：head = [1]
输出：[1]

思路分析：

1. 解法1：迭代

   见算法：链表基础练习篇

2. 解法2：递归

   本题思路与反转链表中的节点思路基本一致，以为无法确定两个节点交换后的第二个节点下一个指针指向哪一个节点，所以依旧需要后序遍历，处理完后面的部分再返回新的头结点

参考代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

class Solution24
{
public:
    ListNode *swapPairs(ListNode *head)
    {
        if (!head || !head->next)
            return head;

        ListNode *newHead = swapPairs(head->next->next);
        ListNode *ret = head->next;
        // 交换逻辑
        head->next->next = head;
        head->next = newHead;

        // 返回新的头结点
        return ret;
    }
};

力扣50.Pow(x, n)¶

力扣50.Pow(x, n)

问题描述：

1
2

输入：x = 2.00000, n = 10
输出：1024.00000

1
2

输入：x = 2.10000, n = 3
输出：9.26100

1
2

输入：x = 2.00000, n = -2
输出：0.25000

思路分析：

1. 解法1：暴力解法

   本题的暴力解法很简单，只需要根据n的值一直让x做乘法

2. 解法2：快速幂

   快速幂就是利用到了折半的思想，使得最后的时间复杂度为\(O(log_{2}{N})\)。具体做法是：

   1. 如果n为偶数，则计算\(x^{\frac{n}{2}}\)，直到n为0返回1
   2. 如果n为奇数，则计算\(x^{\frac{n}{2}}\)时可以分解为\(x^{\frac{n}{2}-1} \times x\)，同样直到n为0返回1

   但是需要注意一个问题，如果n为负数，那么此时计算出的结果应该为x为正数的倒数，所以可以考虑如果n小于0，先让x取其倒数再进行递归，此时不论n初始为正数还是负数，都需要对n取绝对值

关键步骤：

本题需要注意数据溢出的问题，因为如果是\(2^{-31}\)，那么计算的结果就是\(\frac{1}{2^{31}}\)，但是如果是int，最大只能存储\(2^{31}-1\)，所以需要对n进行强制转换为long long

参考代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

class Solution50_2
{
public:
    double myPow(double x, int n)
    {
        if (!n)
            return 1;

        // 处理负数情况：转换为分数进行幂运算
        if (n < 0)
            x = 1 / x;

        // 强转为long long防止-2^31溢出
        double ret = myPow(x, abs((long long) n) / 2);
        // n为奇数时多乘一次x
        return n % 2 == 0 ? ret * ret : ret * ret * x;
    }
};