跳转至

回溯进阶练习

约 2189 个字 405 行代码 3 张图片 预计阅读时间 12 分钟

本篇介绍

在回溯基础练习中已经大致了解到回溯解决的问题，并且在题目中也更深刻理解了前面在回溯理论基础提到的回溯法模板，但是这个模板只是为了便于理解回溯算法，并不能将所有题目都强行为了填充模板而限制了思考，所以为了从模板思路跳脱出来，需要考虑下面的练习

力扣1863.找出所有子集的异或总和再求和

力扣1863.找出所有子集的异或总和再求和

问题描述：

Quote

一个数组的异或总和定义为数组中所有元素按位XOR的结果；如果数组为空，则异或总和为0。

例如，数组[2,5,6]的异或总和为2 XOR 5 XOR 6 = 1。 给你一个数组nums，请你求出nums中每个子集的异或总和，计算并返回这些值相加之和。

注意：在本题中，元素相同的不同子集应多次计数。

数组a是数组b的一个子集的前提条件是：从b删除几个（也可能不删除）元素能够得到a。

示例 1：

C++
1
2
3
4
5
6
7
8
输入：nums = [1,3]
输出：6
解释：[1,3] 共有 4 个子集：
- 空子集的异或总和是 0 。
- [1] 的异或总和为 1 。
- [3] 的异或总和为 3 。
- [1,3] 的异或总和为 1 XOR 3 = 2 。
0 + 1 + 3 + 2 = 6

示例 2：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
输入：nums = [5,1,6]
输出：28
解释：[5,1,6] 共有 8 个子集：
- 空子集的异或总和是 0 。
- [5] 的异或总和为 5 。
- [1] 的异或总和为 1 。
- [6] 的异或总和为 6 。
- [5,1] 的异或总和为 5 XOR 1 = 4 。
- [5,6] 的异或总和为 5 XOR 6 = 3 。
- [1,6] 的异或总和为 1 XOR 6 = 7 。
- [5,1,6] 的异或总和为 5 XOR 1 XOR 6 = 2 。
0 + 5 + 1 + 6 + 4 + 3 + 7 + 2 = 28

示例 3：

C++
1
2
3
输入：nums = [3,4,5,6,7,8]
输出：480
解释：每个子集的全部异或总和值之和为 480 。

思路分析：

本题的基本思路就是求出子集，根据每一个子集求出异或和，最后对所有子集的异或和进行求和，所以基本步骤就是通过变量sum记录所有子集的异或和之和，xorSum记录每一个子集的异或和，为了隐藏异或和的回溯，可以考虑在参数部分使用无副作用运算

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
class Solution1863
{
public:
    int sum = 0;

    void backtracing(vector<int> &nums, int start, int xorSum)
    {
        // 计算当前已经存在的子集的异或和之和，注意xorSum因为是无副作用，所以回溯部分是交给递归完成的
        sum += xorSum;
        for (int i = start; i < nums.size(); i++)
            backtracing(nums, i + 1, xorSum ^ nums[i]);
    }

    int subsetXORSum(vector<int> &nums)
    {
        backtracing(nums, 0, 0);
        return sum;
    }
};

力扣22.括号生成

力扣22.括号生成

问题描述：

Quote

数字n代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且有效的括号组合。

示例 1：

C++
1
2
输入：n = 3
输出：["((()))","(()())","(())()","()(())","()()()"]

示例 2：

C++
1
2
输入：n = 1
输出：["()"]

思路分析：

本题的基本思路是依次枚举当前位置可以填入的括号，因为是括号对，所以一个位置有两种情况：左括号和右括号，假设有三对括号对，那么需要填充的位置就是6个，根据有效的括号对条件：

  1. 左括号数量等于右括号数量
  2. 从第一个括号字符开始，每一个子字符串都满足左括号数量大于等于右括号数量

先枚举左括号，当左括号的个数小于需要的括号对数时，说明还可以添加左括号，否则枚举右括号，当右括号的个数大于等于左括号时，说明右括号不可以再插入。最后，当右括号的个数等于括号对数时，说明已经找到满足要求个数的括号对

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class Solution22
{
public:
    // 记录左括号数量
    int left = 0;
    // 记录右括号数量
    int right = 0;
    string path;
    vector<string> ret;

    void backtracking(int all)
    {
        if (right == all)
        {
            ret.push_back(path);
            return;
        }

        // 有效的括号组合条件：
        // 1. 左括号数量等于右括号数量
        // 2. 从第一个括号字符开始，每一个子字符串都满足左括号数量大于等于右括号数量
        if (left < all) // 当左括号数量小于总数，说明此时还没有足够的括号对
        {
            path += "(";
            left++;
            backtracking(all);
            left--;
            path.pop_back();
        }

        if (right < left) // 当右括号数量小于左括号时就添加右括号，此时左括号已经到达最大数量
        {
            path += ")";
            right++;
            backtracking(all);
            right--;
            path.pop_back();
        }
    }

    vector<string> generateParenthesis(int n)
    {
        backtracking(n);
        return ret;
    }
};

力扣494.目标和

力扣494.目标和

问题描述：

Quote

给你一个非负整数数组nums和一个整数target。

向数组中的每个整数前添加+或-，然后串联起所有整数，可以构造一个表达式：

例如，nums = [2, 1]，可以在2之前添加+，在1之前添加-，然后串联起来得到表达式+2-1。 返回可以通过上述方法构造的、运算结果等于target的不同表达式的数目。

示例 1：

C++
1
2
3
4
5
6
7
8
输入：nums = [1,1,1,1,1], target = 3
输出：5
解释：一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3

示例 2：

C++
1
2
输入：nums = [1], target = 1
输出：1

思路分析：

本题因为每个数字都有两种情况，所以可以理解为两棵二叉树，第一棵二叉树根节点为1，第二棵二叉树根节点为-1，以此类推，根据符号后会出现两种情况：

  1. 当前数值为正数，计算和为sum+nums[i]
  2. 当前数值为负数，计算和为sum-nums[i]

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution494
{
public:
    int count = 0;

    void backtracking(vector<int> &nums, int target, int start, int sum)
    {
        if (start == nums.size())
        {
            if (sum == target)
                count++;
            return;
        }

        // 当取正号
        backtracking(nums, target, start + 1, nums[start] + sum);
        // 当取负号
        backtracking(nums, target, start + 1, sum - nums[start]);
    }

    int findTargetSumWays(vector<int> &nums, int target)
    {
        backtracking(nums, target, 0, 0);

        return count;
    }
};

力扣784.字母大小写全排列

力扣784.字母大小写全排列

问题描述：

Quote

给定一个字符串s，通过将字符串s中的每个字母转变大小写，我们可以获得一个新的字符串。

返回所有可能得到的字符串集合。以任意顺序返回输出。

示例 1：

C++
1
2
输入：s = "a1b2"
输出：["a1b2", "a1B2", "A1b2", "A1B2"]

示例 2:

C++
1
2
输入: s = "3z4"
输出: ["3z4","3Z4"]

思路分析：

本题的基本思路是根据是否需要转变大小写分情况进行递归，如果是字母就走两种递归，一种是大写，另外一种是小写，否则就是数字直接走即可

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution784
{
public:
    vector<string> ret;

    void backtracking(const string &s, int start, string path)
    {
        if (start == s.size())
        {
            ret.push_back(path);
            return;
        }

        // 遇到字母时走两种
        if (isalpha(s[start]))
        {
            backtracking(s, start + 1, path + (char) toupper(s[start]));
            backtracking(s, start + 1, path + (char) tolower(s[start]));
        }
        else
            backtracking(s, start + 1, path + s[start]);
    }

    vector<string> letterCasePermutation(string s)
    {
        backtracking(s, 0, "");

        return ret;
    }
};

力扣526.优美的排列

力扣526.优美的排列

问题描述：

Quote

假设有从1到n的n个整数。用这些整数构造一个数组perm（下标从 1 开始），只要满足下述条件之一，该数组就是一个优美的排列：

  1. perm[i]能够被i整除
  2. i能够被perm[i]整除

给你一个整数n，返回可以构造的优美排列的数量 。

示例 1：

C++
1
2
3
4
5
6
7
8
9
输入：n = 2
输出：2
解释：
第 1 个优美的排列是 [1,2]：
- perm[1] = 1 能被 i = 1 整除
- perm[2] = 2 能被 i = 2 整除
第 2 个优美的排列是 [2,1]:
- perm[1] = 2 能被 i = 1 整除
- i = 2 能被 perm[2] = 1 整除

示例 2：

C++
1
2
输入：n = 1
输出：1

思路分析：

本题的基本思路就是根据优美排列的规则枚举所有可能的情况，但是需要注意，根据给定个数n，第一个位置有n种情况，第二个位置有n-1种情况，以此类推，所以此时就需要涉及到树枝去重，防止在同一个优美排列结果中出现一个数字使用两次的情况。另外，当一个数值无法满足优美排列的条件，就需要枚举后面的值而不是直接跳出循环

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution526
{
public:
    int count = 0;

    void backtracking(int n, int index, vector<bool> &used)
    {
        // index大于n时说明已经到达叶子节点
        if (index > n)
        {
            count++;
            return;
        }

        for (int i = 1; i <= n; i++)
        {
            // 判断当前值是否可以满足优美排列条件之一
            // 满足就可以继续进行递归，否则当前条件直接排除
            if (i % index == 0 || index % i == 0)
            {
                if (used[i])
                    continue;

                used[i] = true;
                backtracking(n, index + 1, used);
                used[i] = false;
            }
            else
                continue; // 当前值不满足优美排列，继续枚举后面的值
        }
    }

    int countArrangement(int n)
    {
        vector<bool> used(n + 1, false);
        backtracking(n, 1, used);

        return count;
    }
};

力扣79.单词搜索

力扣79.单词搜索

问题描述：

Quote

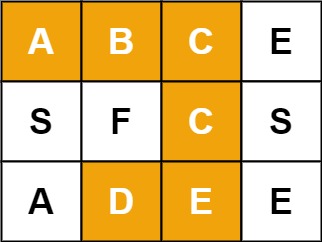
给定一个m x n二维字符网格board和一个字符串单词word。如果word存在于网格中，返回true；否则，返回false。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例 1：

C++
1
2
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

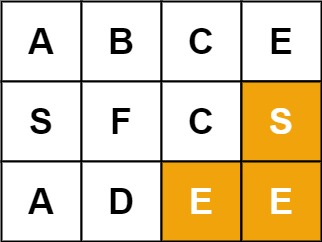
示例 2：

C++
1
2
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
输出：true

示例 3：

C++
1
2
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
输出：false

思路分析：

本题的基本思路是枚举每一个位置，如果当前位置是需要的字符就继续递归查找下一个，否则直接返回false，需要注意的是，因为只有第一个字符需要考虑整个字符表，所以只需要在主函数中使用二维数组遍历找出起始字符，其他的只需要根据相邻字符是否存在进行递归查找即可。因为不能重复走一个位置，所以需要used数组去重

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
class Solution79
{
public:
    bool _exist(vector<vector<char>> &board, int row, int col, int index, const string &word,
                vector<vector<bool>> &used)
    {
        if (index >= word.size())
            return true;

        // 越界直接返回
        if (row < 0 || row >= board.size() || col < 0 || col >= board[0].size())
            return false;

        // 已经使用过的位置不能再使用
        if (used[row][col])
            return false;

        // 当前位置的字符不等于目标字符，直接返回
        if (board[row][col] != word[index])
            return false;

        // 标记当前位置已经使用
        used[row][col] = true;

        // 递归查找
        if (_exist(board, row - 1, col, index + 1, word, used) ||
            _exist(board, row + 1, col, index + 1, word, used) ||
            _exist(board, row, col - 1, index + 1, word, used) ||
            _exist(board, row, col + 1, index + 1, word, used))
            return true;

        used[row][col] = false;

        return false;
    }

    bool exist(vector<vector<char>> &board, string word)
    {
        vector<vector<bool>> used(board.size(), vector<bool>(board[0].size(), false));

        // 枚举起始位置
        for (int i = 0; i < board.size(); i++)
        {
            for (int j = 0; j < board[0].size(); j++)
            {
                if (_exist(board, i, j, 0, word, used))
                    return true;
            }
        }

        return false;
    }
};

力扣1219.黄金矿工

力扣1219.黄金矿工

问题描述：

Quote

你要开发一座金矿，地质勘测学家已经探明了这座金矿中的资源分布，并用大小为m * n的网格grid进行了标注。每个单元格中的整数就表示这一单元格中的黄金数量；如果该单元格是空的，那么就是0。

为了使收益最大化，矿工需要按以下规则来开采黄金：

  1. 每当矿工进入一个单元，就会收集该单元格中的所有黄金。
  2. 矿工每次可以从当前位置向上下左右四个方向走。
  3. 每个单元格只能被开采（进入）一次。
  4. 不得开采（进入）黄金数目为 0 的单元格。
  5. 矿工可以从网格中任意一个有黄金的单元格出发或者是停止。

示例 1：

C++
1
2
3
4
5
6
7
输入：grid = [[0,6,0],[5,8,7],[0,9,0]]
输出：24
解释：
[[0,6,0],
[5,8,7],
[0,9,0]]
一种收集最多黄金的路线是：9 -> 8 -> 7。

示例 2：

C++
1
2
3
4
5
6
7
8
9
输入：grid = [[1,0,7],[2,0,6],[3,4,5],[0,3,0],[9,0,20]]
输出：28
解释：
[[1,0,7],
[2,0,6],
[3,4,5],
[0,3,0],
[9,0,20]]
一种收集最多黄金的路线是：1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7。

思路分析：

本题的基本思路就是固定每一个有效的起点，从该起点出发获取每一条有效路径上的总和，直到求出最大值。因为不能重复走一个位置，所以需要used数组去重

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution1219
{
public:
    int maxVal = INT_MIN;

    int _getMaximumGold(vector<vector<int>> &grid, int row, int col, vector<vector<bool>> &used)
    {
        // 越界或者当前位置为0
        if (row < 0 || row >= grid.size() || col < 0 || col >= grid[0].size() || used[row][col] || grid[row][col] == 0)
            return 0;

        used[row][col] = true;

        // 上
        int top = _getMaximumGold(grid, row - 1, col, used);
        // 下
        int bottom = _getMaximumGold(grid, row + 1, col, used);
        // 左
        int left = _getMaximumGold(grid, row, col - 1, used);
        // 右
        int right = _getMaximumGold(grid, row, col + 1, used);

        // 找到最大的叶子
        int ret = max(max(top, bottom), max(left, right));

        used[row][col] = false;

        return ret + grid[row][col];
    }

    int getMaximumGold(vector<vector<int>> &grid)
    {
        vector<vector<bool>> used(grid.size(), vector<bool>(grid[0].size(), false));

        // 枚举每一个位置
        for (int i = 0; i < grid.size(); i++)
            for (int j = 0; j < grid[0].size(); j++)
                maxVal = max(maxVal, _getMaximumGold(grid, i, j, used));

        return maxVal;
    }
};

力扣980.不同路径Ⅲ

力扣980.不同路径Ⅲ

问题描述：

Quote

在二维网格grid上，有4种类型的方格：

  • 1表示起始方格。且只有一个起始方格。
  • 2表示结束方格，且只有一个结束方格。
  • 0表示我们可以走过的空方格。
  • -1表示我们无法跨越的障碍。

返回在四个方向（上、下、左、右）上行走时，从起始方格到结束方格的不同路径的数目。

每一个无障碍方格都要通过一次，但是一条路径中不能重复通过同一个方格。

示例 1：

C++
1
2
3
4
5
输入：[[1,0,0,0],[0,0,0,0],[0,0,2,-1]]
输出：2
解释：我们有以下两条路径（每个括号内都是经过的元素下标）：
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2)
2. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2)

示例 2：

C++
1
2
3
4
5
6
7
输入：[[1,0,0,0],[0,0,0,0],[0,0,0,2]]
输出：4
解释：我们有以下四条路径： 
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2),(2,3)
2. (0,0),(0,1),(1,1),(1,0),(2,0),(2,1),(2,2),(1,2),(0,2),(0,3),(1,3),(2,3)
3. (0,0),(1,0),(2,0),(2,1),(2,2),(1,2),(1,1),(0,1),(0,2),(0,3),(1,3),(2,3)
4. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2),(2,3)

示例 3：

C++
1
2
3
4
5
输入：[[0,1],[2,0]]
输出：0
解释：
没有一条路能完全穿过每一个空的方格一次。
请注意，起始和结束方格可以位于网格中的任意位置。

思路分析：

本题基本思路就是从起点依次走0的位置，直到找出可以遍历到所有0位置的路径更新计数器即可，需要注意，因为不能重复走一个位置，所以需要使用used数组去重

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
class Solution980
{
public:
    int count = 0;

    // 判断所有0位置是否为true
    bool testZero(const vector<vector<int>> &grid, const vector<vector<bool>> &used)
    {
        for (int i = 0; i < grid.size(); i++)
            for (int j = 0; j < grid[0].size(); j++)
                if (grid[i][j] == 0 && !used[i][j])
                    return false;

        return true;
    }

    void _uniquePathsIII(vector<vector<int>> &grid, int row, int col, vector<vector<bool>> &used)
    {
        if (row < 0 || row >= grid.size() || col < 0 || col >= grid[0].size() || used[row][col] || grid[row][col] == -1)
            return;

        if (grid[row][col] == 2 && testZero(grid, used))
        {
            count++;
            return;
        }

        used[row][col] = true;

        // 上下左右都走一遍
        _uniquePathsIII(grid, row - 1, col, used);
        _uniquePathsIII(grid, row + 1, col, used);
        _uniquePathsIII(grid, row, col - 1, used);
        _uniquePathsIII(grid, row, col + 1, used);

        used[row][col] = false;
    }

    int uniquePathsIII(vector<vector<int>> &grid)
    {
        vector<vector<bool>> used(grid.size(), vector<bool>(grid[0].size(), false));

        // 找到1开始
        for (int i = 0; i < grid.size(); i++)
        {
            for (int j = 0; j < grid[0].size(); j++)
            {
                if (grid[i][j] == 1)
                {
                    _uniquePathsIII(grid, i, j, used);
                }
            }
        }

        return count;
    }
};