贪心基础练习¶
约 5885 个字 705 行代码 3 张图片 预计阅读时间 28 分钟
本篇介绍¶
在贪心理论基础部分已经提到过贪心其实并没有固定的套路,所以贪心的难度也是比较高的。下面的题目彼此关联度也不大,可能存在相似题目,但是不同类型的题目具有不同类型的解题方案,所以不需要刻意去背题目,而是需要理解题目的基本逻辑
力扣455.分发饼干¶
问题描述:
Quote
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
对每个孩子i,都有一个胃口值g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干j,都有一个尺寸s[j]。如果s[j] >= g[i],我们可以将这个饼干j分配给孩子i,这个孩子会得到满足。你的目标是满足尽可能多的孩子,并输出这个最大数值。
示例 1:
| C++ | |
|---|---|
1 2 3 4 5 6 | |
示例 2:
| C++ | |
|---|---|
1 2 3 4 5 6 | |
思路分析:
首先理解题目的要求:保证当前饼干的尺寸可以满足孩子的胃口,也就是说,可能存在孩子的胃口大于当前饼干的尺寸,所以考虑遍历饼干
当遇到一个饼干尺寸大于等于孩子的胃口时,就更新孩子数组的下标,但是此时就会出现一个问题:当饼干数组的大小小于孩子数组的大小时,如果饼干数组中所有的元素均小于孩子数组对应的元素,但是孩子数组剩余的元素存在小于饼干数组的元素时就会出现遗漏,所以考虑对两个数组都进行排序,确保可以满足大的饼干优先喂给胃口小的孩子,这样就不会出现遗漏计算,因为一旦大尺寸的饼干喂给了小胃口的孩子,那么当前尺寸的饼干之前的饼干一定是没有意义的,所以继续向后遍历即可,而孩子数组只需要更新下标到下一个孩子,即一旦饼干满足胃口就更新下标
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | |
力扣376.摆动序列¶
问题描述:
Quote
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 摆动序列 。第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。
例如,[1, 7, 4, 9, 2, 5]是一个 摆动序列 ,因为差值(6, -3, 5, -7, 3)是正负交替出现的。
相反,[1, 4, 7, 2, 5]和[1, 7, 4, 5, 5]不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。 子序列 可以通过从原始序列中删除一些(也可以不删除)元素来获得,剩下的元素保持其原始顺序。
给你一个整数数组nums,返回nums中作为 摆动序列的最长子序列的长度 。
示例 1:
| C++ | |
|---|---|
1 2 3 | |
| C++ | |
|---|---|
1 2 3 4 | |
示例 3:
| C++ | |
|---|---|
1 2 | |
思路分析:
解决本题之前先要理解本题的意思,本题中所谓的摆动序列,实际上就是确定当前值为局部峰值:
- 当前值-左侧值大于或者小于0
- 右侧值-当前值小于或者大于0
满足上面两个条件就说明当前数值在左右两个数值之间属于峰值
根据这个特点,可以考虑下面的情况:
- 持续递增/递减无平坡
- 递增/递减存在平坡
- 只有两个彼此不同的元素
- 从某点平坡再持续递增
首先考虑第一种情况,以[1,17,5,10,13,15,10,5,16,8]为例,在第一个5变化到10之后,10的后面是13,此时的5开始就是持续递增无平坡的情况,直到遇到15,而以为10的左右两侧只有左侧满足递增,所以需要考虑“删除元素”,直到15为止,当抵达15元素时,再遇到第二个10时,又出现了持续递减无平坡的情况,同样,去除10直到5
对于第二种情况,以[1,2,2,2,1]为例,当1进入第一个2时,此时的2左侧存在递增,但是右侧并不是递增,所以并没有满足局部峰值的条件,需要“删除元素”,直到最后一个2元素
对于第三种情况,以[1,2]为例,当1进入2时,左侧存在一个递增,但是右侧已经没有了数据,根据题目要求:仅有一个元素或者含两个不等元素的序列也视作摆动序列,所以可以考虑直接写死,也可以考虑默认给定一个序列值为1,并在该基础上改变
对于第四种情况,以[1,2,2,2,3,4]为例,可以看到从1到第一个2存在坡度,但是后面先平坡再递增,此时就需要注意更新第一个坡度的时机,因为平坡过程中,第一个坡度值一直为0直到遇到最后一个2时,两次的坡度改变,变为第二种情况。但是,此时并不应该修改第一个坡度值,因为第二次的坡度改变依旧是递增趋势
根据上面4种情况,可以分析出下面的逻辑:
- 首先确定结果变量,初始化为1,表示默认存在一个坡度
- 接着通过两个变量
prediff和curdiff记录前一个坡度和后一个坡度 - 根据条件
prediff<0 && curdiff>0或者prediff > 0 && curdiff < 0(处理第一种情况)或者prediff == 0 && curdiff < 0或者prediff == 0 && curdiff > 0(第二种情况) - 先计算
curdiff=nums[i + 1] - nums[i],为了防止prediff因为第4种情况时更新成了0,考虑在判断条件成立时更新prediff=curd
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | |
力扣53.最大子数组和¶
问题描述:
Quote
给你一个整数数组nums,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组是数组中的一个连续部分。
示例 1:
| C++ | |
|---|---|
1 2 3 | |
示例 2:
| C++ | |
|---|---|
1 2 | |
示例 3:
| C++ | |
|---|---|
1 2 | |
思路分析:
本题还是考虑使用局部最优推出全局最优的思路,考虑到如果当前和为负数时,那么不论下一个数是否是正数,都更新到下一个数,此时需要做到每一次计算和都保存一次和的最大值,如果当前和小于0,更新sum到新的数。此时存在两种情况:
- 当前为负数,此时因为结果变量
ret已经存了上一次计算的和,如果当前为负数那么哪怕是小于当前sum的数也不会影响到最终结果 - 当前为正数,因为正数相加只会越来越大,如果
sum为负数,那么与其加上正数,不如直接使用正数
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | |
力扣121.买卖股票的最佳时机¶
问题描述:
Quote
给定一个数组prices,它的第i个元素prices[i]表示一支给定股票第i天的价格。
你只能选择某一天买入这只股票,并选择在未来的某一个不同的日子卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回0。
示例 1:
| C++ | |
|---|---|
1 2 3 4 | |
示例 2:
| C++ | |
|---|---|
1 2 3 | |
思路分析:
本题可以考虑思路:如果购买时的价格与卖出时的价格之差小于0,说明买的时候买贵了,此时不论后面怎么卖都不可能出现比下一次买利润多,所以可以推出下面的情况:如果当前利润小于0,说明如果在下一次买入可能会获得更大利润,此时只需要更新指针指向下一次买入的价格即可,如果当前利润大于0,说明已经存在可用利润,此时只需要更新遍历的指针,每一次遍历求出最大利润即可
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | |
力扣122.买卖股票的最佳时机Ⅱ¶
问题描述:
Quote
给你一个整数数组prices,其中prices[i]表示某支股票第i天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候最多只能持有 一股 股票。你也可以先购买,然后在同一天出售。
返回你能获得的最大利润。
示例 1:
| C++ | |
|---|---|
1 2 3 4 5 | |
示例 2:
| C++ | |
|---|---|
1 2 3 4 | |
示例 3:
| C++ | |
|---|---|
1 2 3 | |
思路分析:
通过上一题的理解,可以知道本题的大致意思,接着考虑本题的思路:
考虑一个等式:假设i,j,k分别表示三个连续的下标,那么区间之差p[k]-p[i] = p[k]-p[j] + p[j]-p[i]
通过上面这个等式,以[7,1,5,3,6,4]为例,假设买入的是下标为1的股票,卖出时价格为下标为4的元素,那么p[4]-p[1] = p[4]-p[3]+p[3]-p[2]+p[2]-p[1] = 3 + -2 + 4 = 5。也就是说,如果可以求出连续的差之和最大那么最后的利润就是最大的,即相邻元素之差之和最大即可获得最大利润,此时就可以考虑何时使相邻元素之差之和最大,很明显,如果相邻元素之差为负数,那么此时和肯定会减小,所以只需要做到相邻元素之和为正数时累加即可获得最大利润
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | |
力扣55.跳跃游戏¶
问题描述:
Quote
给你一个非负整数数组nums,你最初位于数组的第一个下标。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标,如果可以,返回true;否则,返回false。
示例 1:
| C++ | |
|---|---|
1 2 3 | |
示例 2:
| C++ | |
|---|---|
1 2 3 | |
思路分析
本题的基本思路就是找到可以走到结尾的步数,为了可以走到结尾,所以步数要尽可能得大,而要使步数尽可能大,局部最优就是每一次走的步数尽可能大,从第一步开始,如果下一个元素大于剩余的步数,就直接更新步数,否则就继续向下走,如果走到元素为0的位置时,存在三种情况:
- 已经是最后一个元素
- 步数没有走完
- 步数走完并且没有到最后一个元素
根据上面三种情况可以得出只有最后一种情况是需要返回false的,其他均返回true
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | |
力扣45.跳跃游戏Ⅱ¶
问题描述:
Quote
给定一个长度为n的 0 索引整数数组nums。初始位置为nums[0]。
每个元素nums[i]表示从索引i向后跳转的最大长度。换句话说,如果你在nums[i]处,你可以跳转到任意nums[i + j]处:
0 <= j <= nums[i]i + j < n返回到达nums[n - 1]的最小跳跃次数。生成的测试用例可以到达nums[n - 1]。
示例 1:
| C++ | |
|---|---|
1 2 3 4 | |
示例 2:
| C++ | |
|---|---|
1 2 | |
思路分析:
本题的基本思路是找出最大可以覆盖的范围从而减少跳跃的次数,分为两种情况:
- 当前位置+当前位置的步数可以覆盖到结尾
- 当前位置+当前位置的步数不可以覆盖到结尾
先记录一下当前位置+当前位置的步数,如果该值大于下一次要走的步数,就更新该值,接着判断当前位置是否已经到当前步数的终点位置,此时分为两种情况:
- 已经到当前步数的终点位置
- 没有到当前步数的重点位置
对于第一种情况也分为两种情况:
- 当前位置并不是最后一个元素的位置
- 当前位置已经是最后一个元素的位置
对于此时的第一种情况来说就需要更新到下一次的步数,因为贪的是最大的覆盖范围,所以更新到下一次最大可以走的步数值,并更新跳跃次数。最后返回跳跃次数即可
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 | |
力扣1005.K次取反后最大化的数组和¶
Quote
给你一个整数数组nums和一个整数k,按以下方法修改该数组:
选择某个下标i并将nums[i]替换为-nums[i]。 重复这个过程恰好k次。可以多次选择同一个下标i。
以这种方式修改数组后,返回数组 可能的最大和 。
示例 1:
| C++ | |
|---|---|
1 2 3 | |
示例 2:
| C++ | |
|---|---|
1 2 3 | |
示例 3:
| C++ | |
|---|---|
1 2 3 | |
思路分析:
本题的基本思路就是先对数组中的至多k个绝对值较大的负数进行取反,如果负数个数小于k,那么再对最小的正数进行多次取反直到k用完。根据这个思路可以看出,本题用到了两次贪心,第一次贪绝对值较大的负数,第二次贪绝对值较小的非负整数:对于第一次贪,考虑先对数组按照绝对值较大者优先进行排序,当遇到负数时,对其进行取反并减小一次k值,直到没有负数或者k用完为止;对于第二次贪,只需要找到最小的非负整数一直取反直到用完k为止,此处可以考虑用循环一直对一个数进行取反,但是也可以考虑取反的周期性,如果k为奇数,那么进行k次取反,结果一定是原来数值的相反数,否则k不变
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 | |
力扣134.加油站¶
Quote
在一条环路上有n个加油站,其中第i个加油站有汽油gas[i]升。
你有一辆油箱容量无限的的汽车,从第i个加油站开往第i+1个加油站需要消耗汽油cost[i]升。你从其中的一个加油站出发,开始时油箱为空。
给定两个整数数组gas和cost,如果你可以按顺序绕环路行驶一周,则返回出发时加油站的编号,否则返回-1。如果存在解,则保证它是唯一的。
示例 1:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 | |
示例 2:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 | |
思路分析:
本题的暴力思路是模拟每一个位置作为起点判断是否可以走到终点,但是时间复杂度比较高,考虑使用贪心。本题主要贪的就是当前位置及之前的和是否是对油量有增益效果(即加的油和最后消耗的油之和是否大于0),如果没有,就到下一个位置继续查找,如果总和都是消耗效果,那么说明不存在该起点
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | |
力扣135.分发糖果¶
问题描述:
Quote
n个孩子站成一排。给你一个整数数组ratings表示每个孩子的评分。
你需要按照以下要求,给这些孩子分发糖果:
- 每个孩子至少分配到 1 个糖果。
- 相邻两个孩子评分更高的孩子会获得更多的糖果。
请你给每个孩子分发糖果,计算并返回需要准备的最少糖果数目。
示例 1:
| C++ | |
|---|---|
1 2 3 | |
示例 2:
| C++ | |
|---|---|
1 2 3 4 | |
思路分析:
本题的基本思路可以说是根据题目要求进行模拟更改糖果的数量,但是需要注意,本题因为既要考虑当前位置比其左侧孩子大时,当前位置的糖果较多,也要考虑当前位置比其右侧孩子大时,当前位置的糖果较多,所以本题实际上要考虑两边的情况,对于这种需要考虑两边的情况时,不建议一次性同时考虑两边,而是先考虑一边,再利用已经考虑过的结果反向遍历考虑另一边。这里需要注意,考虑第二边不可以是正向遍历,因为第二边本质是要找到最右侧不符合条件的情况,如果依旧是正向遍历,就相当于从第一边考虑第二种情况
例如对于[1,2,2,5,4,3,2]来说,第一遍计算糖果如下:
| Text Only | |
|---|---|
1 2 | |
第二遍计算糖果如下:
| Text Only | |
|---|---|
1 2 | |
很明显,在第二边正向中,因为5>4,所以5的位置需要更新到4的糖果数量+1的结果,也就是2,同理可得后面的元素,但是如果是逆向,就是先处理第一个不满足条件的情况,再依次处理第二个乃至最后一个
另外还需要注意,在考虑第二边时,需要取计算糖果和原始糖果的最大值作为新糖果值,防止出现例如[1,3,4,5,2],第一边处理结果为[1,2,3,4,1],因为此时在第二边没处理,如果没有取最大值就会导致[...5,2]时,5的位置被覆盖为2的糖果数量1+1覆盖第一边的4的情况导致错误
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | |
力扣860.柠檬水找零¶
问题描述:
Quote
在柠檬水摊上,每一杯柠檬水的售价为5美元。顾客排队购买你的产品,(按账单bills支付的顺序)一次购买一杯。
每位顾客只买一杯柠檬水,然后向你付5美元、10美元或20美元。你必须给每个顾客正确找零,也就是说净交易是每位顾客向你支付5美元。
注意,一开始你手头没有任何零钱。
给你一个整数数组bills,其中bills[i]是第i位顾客付的账。如果你能给每位顾客正确找零,返回true,否则返回false。
示例 1:
| C++ | |
|---|---|
1 2 3 4 5 6 7 | |
示例 2:
| C++ | |
|---|---|
1 2 3 4 5 6 7 | |
思路分析:
本题就是按照题目的要求去模拟,一共有三种情况:
- 收到面值为5,直接收下
- 收到面值为10,找面值5
- 收到面值为20,可以找10和5,也可以找3个5,但是优先10和5,因为5更通用
注意,本题不需要考虑具体的计算,例如找零还剩多少钱,只需要确定是否还可以正确找零即可,对于这种情况,只需要记录可以用来找零的面值个数是否足够即可
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 | |
力扣406.根据身高重建队列¶
问题描述:
Quote
假设有打乱顺序的一群人站成一个队列,数组people表示队列中一些人的属性(不一定按顺序)。每个people[i] = [hi, ki]表示第i个人的身高为hi,前面 正好有ki个身高大于或等于hi的人。
请你重新构造并返回输入数组people所表示的队列。返回的队列应该格式化为数组queue,其中queue[j] = [hj, kj]是队列中第j个人的属性(queue[0] 是排在队列前面的人)。
示例 1:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 | |
示例 2:
| C++ | |
|---|---|
1 2 | |
思路分析:
因为本题需要满足前面正好有k个身高大于或等于h的人,所以首先考虑对原数组按照身高降序进行排序(如果身高相同就按照k进行升序排序),这样排序后就可以确保任何一个元素之前的元素都是身高比当前元素大的,此时的k就代表了插入的位置,例如如果说一个元素的k为1,表示其之前只有一个元素的身高比当前元素的身高大,那么就可以插入到k所在的下标位置,因为下标为1之前只有一个元素(即下标为0的元素),同理可得其他元素
代码优化:
因为vector插入元素时涉及到挪动数据和扩容,这两者消耗比较大,所以考虑先用list完成插入操作,再通过list构造vector返回
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | |
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | |
力扣452.用最少数量的箭引爆气球¶
问题描述:
Quote
有一些球形气球贴在一堵用XY平面表示的墙面上。墙面上的气球记录在整数数组points,其中points[i] = [xstart, xend]表示水平直径在xstart和xend之间的气球。你不知道气球的确切y坐标。
一支弓箭可以沿着x轴从不同点 完全垂直 地射出。在坐标x处射出一支箭,若有一个气球的直径的开始和结束坐标为xstart,xend, 且满足xstart ≤ x ≤ xend,则该气球会被 引爆 。可以射出的弓箭的数量没有限制。弓箭一旦被射出之后,可以无限地前进。
给你一个数组points,返回引爆所有气球所必须射出的最小弓箭数 。
示例 1:
| C++ | |
|---|---|
1 2 3 4 5 | |
示例 2:
| C++ | |
|---|---|
1 2 3 | |
示例 3:
| C++ | |
|---|---|
1 2 3 4 5 | |
思路分析:
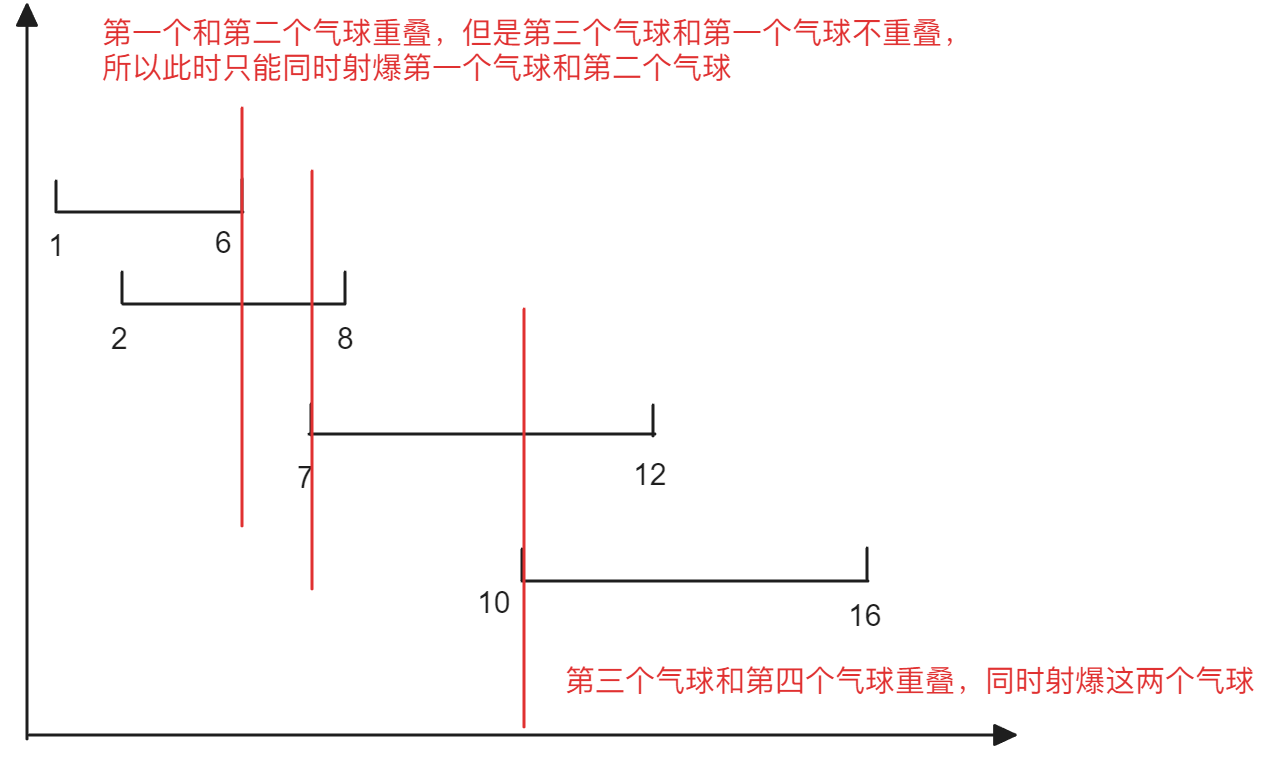
本题的基本思路就是找出尽可能让可以用一支箭矢射爆的气球聚集在一起(即气球是否重叠),要判断是否重叠首先就需要对所有气球进行排序,可以按照左边界排序,也可以按照右边界排序。下面以按照左边界排序为例,排序完后,相邻的气球就可以通过判断当前气球的左边界和上一个气球的右边界是否重叠决定是否需要增加箭矢,接下来是本题的细节,除了判断当前气球和上一个气球是否重叠外,还需要判断下一个气球是否和当前或者上一个气球重叠,如果不重叠就依旧需要增加箭矢,判断方式就是找到当前气球和上一个气球的最小右边界,只要大于这个最小右边界就可以满足不需要增加箭矢而使用同一支箭矢射爆气球。以示例一为例,示意图如下:
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 | |
力扣435.无重叠区间¶
问题描述:
Quote
给定一个区间的集合intervals,其中intervals[i] = [starti, endi]。返回 需要移除区间的最小数量,使剩余区间互不重叠 。
注意只在一点上接触的区间是不重叠的。例如[1, 2]和[2, 3]是不重叠的。
示例 1:
| C++ | |
|---|---|
1 2 3 | |
示例 2:
| C++ | |
|---|---|
1 2 3 | |
示例 3:
| C++ | |
|---|---|
1 2 3 | |
思路分析:
本题思路与上一题思路非常类似,不同的是,本题不考虑等于的情况,即比较左边界是否小于上一个元素的右边界作为判断重叠的条件。如果满足重叠条件,就更新计数器,并且因为要判断下一个区间是否依旧重叠,需要更新右边界为较小的右边界,这一步更新就相当于移除当前导致重叠的区间,让新区间和旧区间再做一次判断是否重叠
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | |
力扣56.合并区间¶
问题描述:
Quote
以数组intervals表示若干个区间的集合,其中单个区间为intervals[i] = [starti, endi]。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
| C++ | |
|---|---|
1 2 3 | |
示例 2:
| C++ | |
|---|---|
1 2 3 | |
思路分析:
本题与前两题思路也非常类似,依旧是判断当前区间的左边界是否小于等于上一区间的右边界作为判断重叠条件。如果满足重叠,就需要合并区间,需要注意,默认情况下,返回值数组中有一个起始区间,合并区间之前需要先弹出前一个区间,并更新新的区间的左边界为前一个区间的左边界和当前区间的左边界中的最小值,同理更新新的区间的右边界为前一个区间的右边界和当前区间的右边界的最大值,此时也可以确保下一次比较是按照新区间和当前区间进行比较从而不会遗漏情况,如果没有重叠就直接插入当前区间即可
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 | |
力扣763.划分字母区间¶
问题描述:
Quote
给你一个字符串s。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。
注意,划分结果需要满足:将所有划分结果按顺序连接,得到的字符串仍然是s。
返回一个表示每个字符串片段的长度的列表。
示例 1:
| C++ | |
|---|---|
1 2 3 4 5 6 | |
示例 2:
| C++ | |
|---|---|
1 2 | |
思路分析:
本题最容易想到的就是找到最大区间边界,判断哪些字母的最远位置小于等于最远区间边界就囊括这些字母放在一个区间中,所以就需要先统计每个字母最远出现的位置。接着就是再一次遍历整个字符串,遍历的过程中不断更新最远区间边界,确保其可以囊括当前字母,一旦当前位置等于最远区间边界就说明已经找到一个区间
本题获取到每个字母最远出现的位置后,不要考虑仅根据每个字母最远出现的位置进行分割,因为单看这个位置值无法确定何时差值为一个合理值,他们之间本身没有直接的关系,有关系的应该是每个字母的当前下标和当前字母之前的最远区间边界值,如果当前下标小于最远边界值,那么就一定说明后面还出现过当前字母之前的字母,所以考虑完统计每个字母最远出现的位置后,应该考虑遍历原字符串而不是仅仅死磕每个字母的出现位置,从而将每个字母的当前位置和最远出现位置联系起来
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 | |
力扣738.单调递增的数字¶
问题描述:
Quote
当且仅当每个相邻位数上的数字x和y满足x <= y时,我们称这个整数是单调递增的。
给定一个整数n,返回小于或等于n的最大数字,且数字呈单调递增。
示例 1:
| C++ | |
|---|---|
1 2 | |
示例 2:
| C++ | |
|---|---|
1 2 | |
示例 3:
| C++ | |
|---|---|
1 2 | |
思路分析:
本题的思路就是判断当前位置的值是否比前一位值大或者相等,如果不满足这个条件说明需要更新,更新的方式就是前一位减小1个单位,当前位修改为9,之所以当前位需要修改为9是因为如果不满足单调递增,就需要取出小于等于当前数值的最大数值。
需要注意本题的细节: 1. 将数值转换为字符串而非取出每个数字插入到数组中,这样可以快速地得到可以用下标操作的字符串数组 2. 逆序遍历字符串数组,这样可以确保从后向前,让下一次的比较可以利用到上一次的比较结果 3. 在找到需要修改为9的位置时并不是直接修改,而是先标记需要修改为9的起始位置,这样可以确保遇到类似1000的数值时可以正确处理,因为后两位满足小于等于的条件,但是10不满足,如果直接修改为9,就会出现最后值为900而不是999 4. 用于标记9的起始位置变量初始化为字符串数组的长度而不是其他值,防止出现本身已经满足单调递增的条件的数值全部被覆盖为9
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 | |
力扣968.监控二叉树¶
问题描述:
Quote
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:
| C++ | |
|---|---|
1 2 3 | |
示例 2:
| C++ | |
|---|---|
1 2 3 | |
思路分析:
本题分析题意可以发现,一个有摄像头的节点可以覆盖其父亲节点和其孩子节点,所以可以推出节点的三种状态(数字编号为代码中的状态编号):
- 无覆盖
- 已经安装摄像头
- 有覆盖
根据上面节点的三种状态可以推出三种情况:
- 当前节点没有摄像头,但是其孩子节点是被全覆盖的情况,此时说明这两个节点已经被这两个节点的孩子节点覆盖,那么当前节点就是无覆盖的情况,属于情况0,所以此时需要告诉其父亲节点需要添加摄像头
- 当前节点至少存在一个孩子没有被覆盖,此时尽管另外一个孩子被覆盖了,但是因为有一个孩子没有被覆盖,所以当前节点需要添加一个摄像头,并向上层返回情况1表示已经添加了摄像头
- 当前节点至少存在一个孩子有摄像头,此时不论是哪个孩子有摄像头,当前节点一定是被覆盖的情况,所以向上层返回情况2即可
针对上面三种情况可以看出,首先就是要确定孩子节点的状态,所以需要使用到后序遍历,根据左孩子和右孩子的状态确定当前节点的状态,再决定是否要安装摄像头。需要额外注意一种特殊情况,就是根节点刚好处于没有覆盖的情况,此时就需要单独处理,如果根节点是情况0,那么就需要再添加一个摄像头
参考代码:
| C++ | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 | |