map和set类模拟实现¶

约 2180 个字 445 行代码 5 张图片预计阅读时间 13 分钟

map和set模拟实现介绍¶

在C++的STL标准库中，map和set的底层均为红黑树，所以在前面的红黑树实现基础上模拟封装map和set类

map和set类定义¶

首先，通过查看SGI版本的STL中对map和set的设计可以看到不论是map还是set都在红黑树结构传递的是Key和Value，而不是额外设计两种版本的红黑树结构

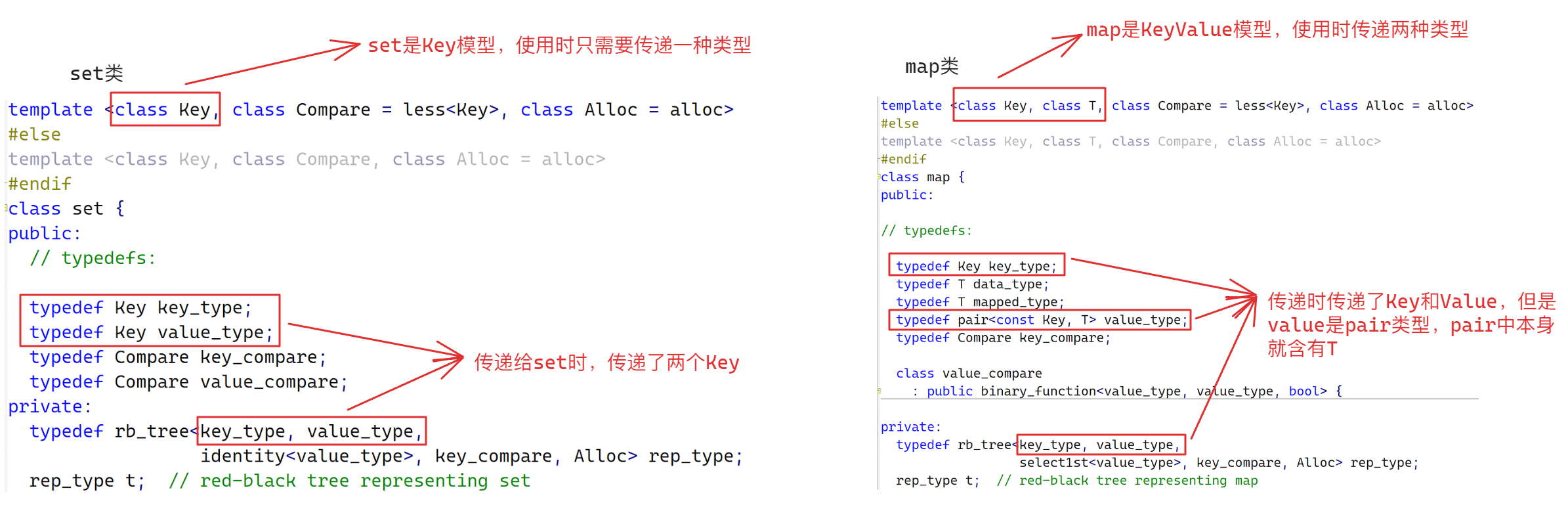
观察红黑树结构的模版参数设计

实际上，SGI版本在设计map和set时，为了同时使一种红黑树可以实例化出两种容器，将set的Key多传递了一次，所以对于set来说，传递给红黑树的参数应该为：

C++
template <Key, Key> // 只展示部分
class rb_tree

而对于map来说，传递的参数应该为：

C++
template <Key, pair<const Key, T>> // 只展示部分
class rb_tree

对于find函数需要Key进行查找，但是不需要使用到value，所以在查找时可以直接使用第一个参数Key；而对于insert来说，插入的可能就不只是一个Key而是一个Key_Value，所以第一个Key参数给find函数使用，而第二个参数给insert使用

为了模拟出SGI版本中的形式，可以将模拟实现的map和set类的模版参数定义为

C++
// map
template<class Key, class T>
class map
{
private:
    RBTree<Key, pair<Key, T>> rb_t;
};

// set
template <class T>
class set
{
private:
    RBTree<T, T> rb_t;
};

对应的红黑树节点构造应该是用第二个模版参数类型的变量进行构造，因为第一个模版参数的变量用于find函数，此时对于set来说，红黑树的节点的值类型就是Key，而对于map来说就是pair<key, T>类型，修改红黑树节点结构和红黑树结构如下：

C++
// 定义树每一个节点结构
template<class T>
struct RBTreeNode
{
    T _data;
    // 左子树指针
    RBTreeNode<T>* _left;
    // 右子树指针
    RBTreeNode<T>* _right;
    // 父亲节点指针
    RBTreeNode<T>* _parent;
    Color _col;

    //单个节点构造函数
    RBTreeNode(const T& data)
        : _data(data)
        , _left(nullptr)
        , _right(nullptr)
        , _parent(nullptr)
        , _col(Red)
    {}
};

// 红黑树结构
template<class T, class V>
class RBTree
{
    // 定义节点
    typedef RBTreeNode<V> node;// 利用第二个模版参数进行构造
private:
    // 根节点
    node* _root;
};

map和set类的遍历比较规则设计¶

对于set的insert函数来说，只需要比较key即可，如果使用模版参数中的T类型变量data直接进行比较，此时没有任何问题，但是如果是map，则此时会对pair进行比较，而pair本身支持的比较是先比较first，再比较second，这与本身二叉搜索树的遍历比较规则不符，所以此时需要额外处理

观察SGI版本中的设计，存在一个KeyOfValue的一个模版参数，该参数的作用是处理遍历比较规则问题

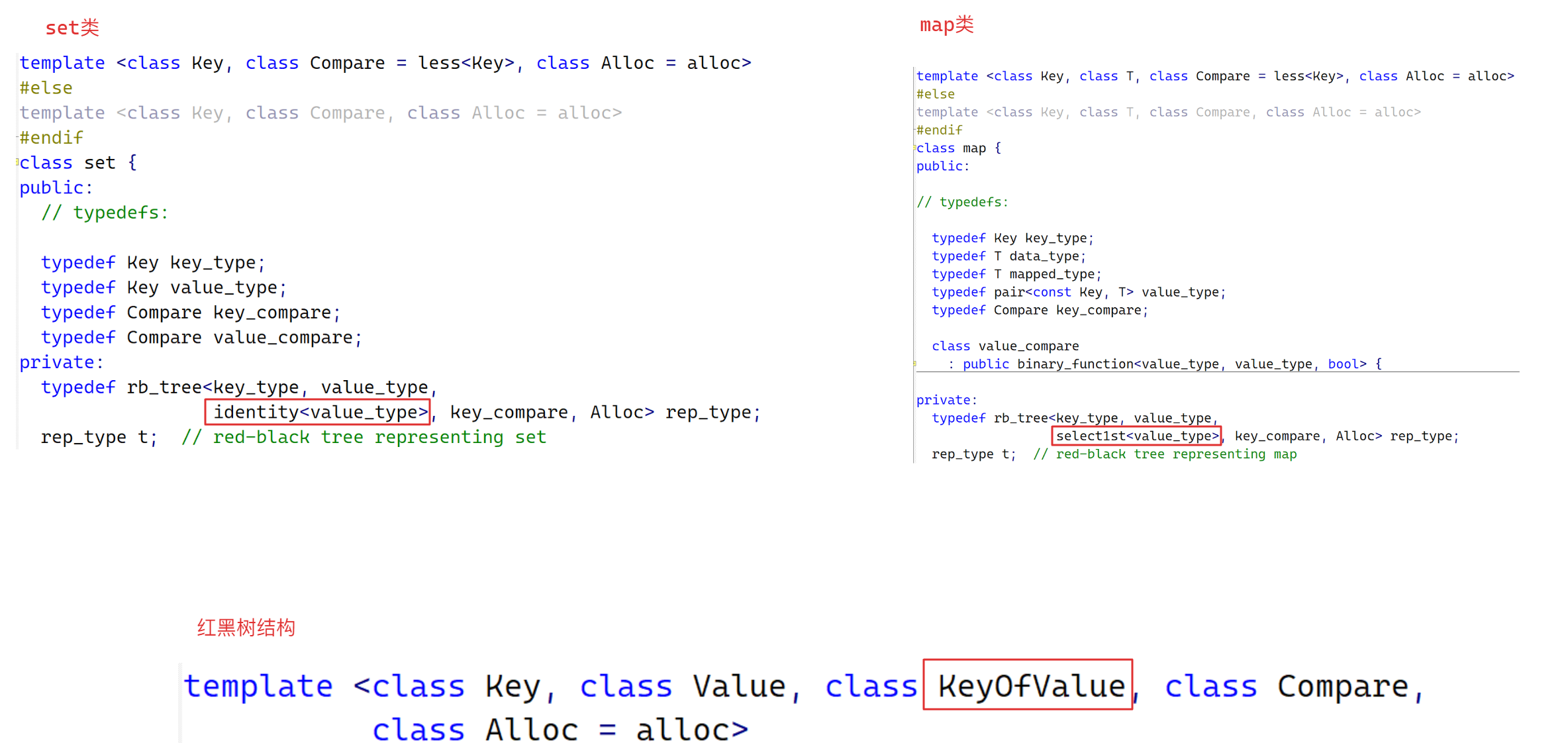
因为在红黑树结构中本身并不知道传递的到底是什么类型，但是对于set和map来说知道，所以可以通过set和map传递给红黑树结构，为了使比较方式统一，可以在set中定义一个仿函数，该仿函数返回一个Key类型的值，对于map来说，返回一个pair的first值

C++
// set
// 返回set的key
struct setKeyOfT
{
    const T& operator()(const T& key)
    {
        return key;
    }
};

// map
// 返回map的pair的first
struct mapKeyOfV
{
    const Key& operator()(const pair<Key, T>& kv)
    {
        return kv.first;
    }
};

// 通过模版参数传递
// set
RBTree<T, T, setKeyOfT> rb_t;
// map
RBTree<Key, pair<Key, T>, mapKeyOfV> rb_t;

因为传递的两个模版参数是一个仿函数，在insert函数中使用该类型创建一个对象，调用对应重载的函数获取其返回值进行比较

C++
// 创建仿函数对象获取内容
KeyOfV kov;

// 根据KeyOfV类型对应调用对应的重载函数
if (kov(data) > kov(cur->_data))
{
    // 大于根节点数据，插入在右子树，走到左子树的空位置
    // ...
}
else if (kov(data) < kov(cur->_data))
{
    // 小于根节点数据，插入在左子树，走到右子树的空位置
    // ...
}

map和set中的常规迭代器设计¶

常规迭代器结构定义¶

因为map和set底层都是红黑树，所以直接设计红黑树的迭代器即可

C++
template <class V>
struct RBTree_iterator
{
    typedef RBTreeNode<V> node;

    // 构造迭代器
    RBTree_iterator(node* node)
        : _node(node)
    {}

    node* _node;
};

`operator*()`设计¶

该函数直接返回对应节点的数据即可，所以可以设计为：

C++
V& operator*()
{
    return _node->_data;
}

`operator->()`设计¶

该函数返回对应节点的地址即可，可以设计为：

C++
V* operator->()
{
    return &_node->_data;
}

`operator!=()`设计¶

该函数用于判断两个节点是否相等，只需要判断两个节点的指针位置是否相等即可

C++
bool operator!=(const RBTree_iterator& node)
{
    return _node != node._node;
}

`operator==()`设计¶

该函数用于判断两个节点是否相等，只需要判断两个节点的指针位置是否相等即可

C++
bool operator== (const Self& s)
{
    return _node == s._node;
}

`operator++()`设计¶

该函数用于进行迭代器更新，但是此处需要使用循环进行解决，首先因为二叉搜索树的遍历是中序遍历，所以先走左子树，并且第一个数值是左子树的最左节点，所以可以通过循环先获取到最左节点，该最左节点作为红黑树迭代器的begin()位置

C++
Iterator Begin()
{
    // 找到最左节点
    node* leftMost = _root;
    while (leftMost && leftMost->_left)
    {
        leftMost = leftMost->_left;
    }

    // 返回最左节点作为起始位置
    return Iterator(leftMost);
}

对于end()来说，可以返回一个nullptr，因为是中序遍历，当根为空时最左节点也为空，当根不为空时，走到根节点的父亲也为空

C++
Iterator End()
{
    return Iterator(nullptr);
}

接下来设计operator++()函数，因为中序遍历的顺序是左子树->根->右子树，所以走到某一个节点时，将该节点及其子树作为一个部分整体，因为从当前节点位置开始遍历时不需要访问该节点前面的节点，所以可以不用考虑当前节点的左子树，接着考虑右子树，当右子树不为空时，找到右子树的根节点，走该子树的左子树找到最左节点作为下一个节点；

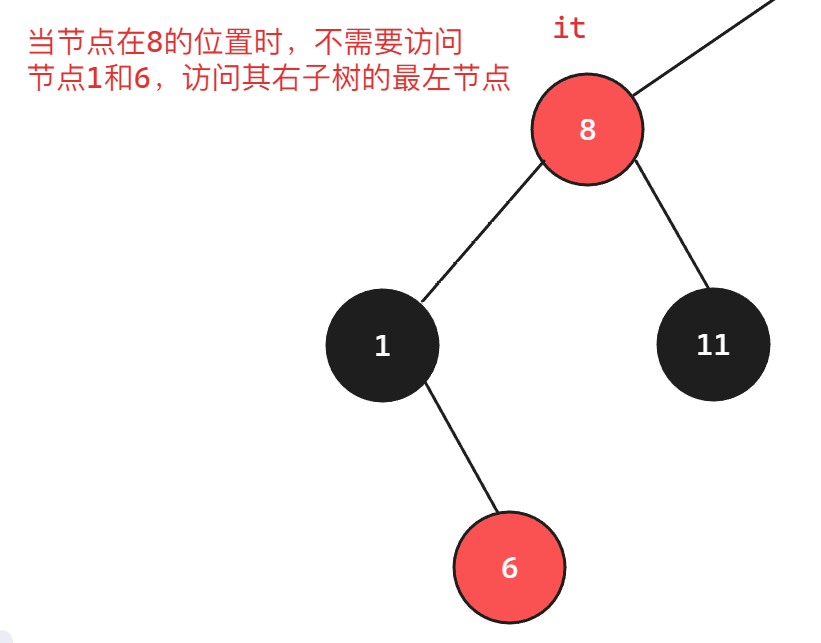
访问完最左节点后，下一个节点是当前子树的根节点，以当前节点为根节点，因为找到的是最左节点，所以其左子树一定为空，但是其右子树可能不一定，如果右子树依旧不为空，则继续上面的步骤，如果右子树此时为空，说明当前子树已经访问完毕。因为右子树不为空的时候进入了右子树，根据中序顺序左子树->根->右子树，说明当前右子树的根节点已经遍历到，接下来应该要取到当前子树的根节点的父亲节点，如果当前节点依旧是新父亲节点的右孩子，则继续向上更新父亲节点，直到遇到父亲节点为空结束，否则按照顺序接下来遍历根，再右子树，如此往复

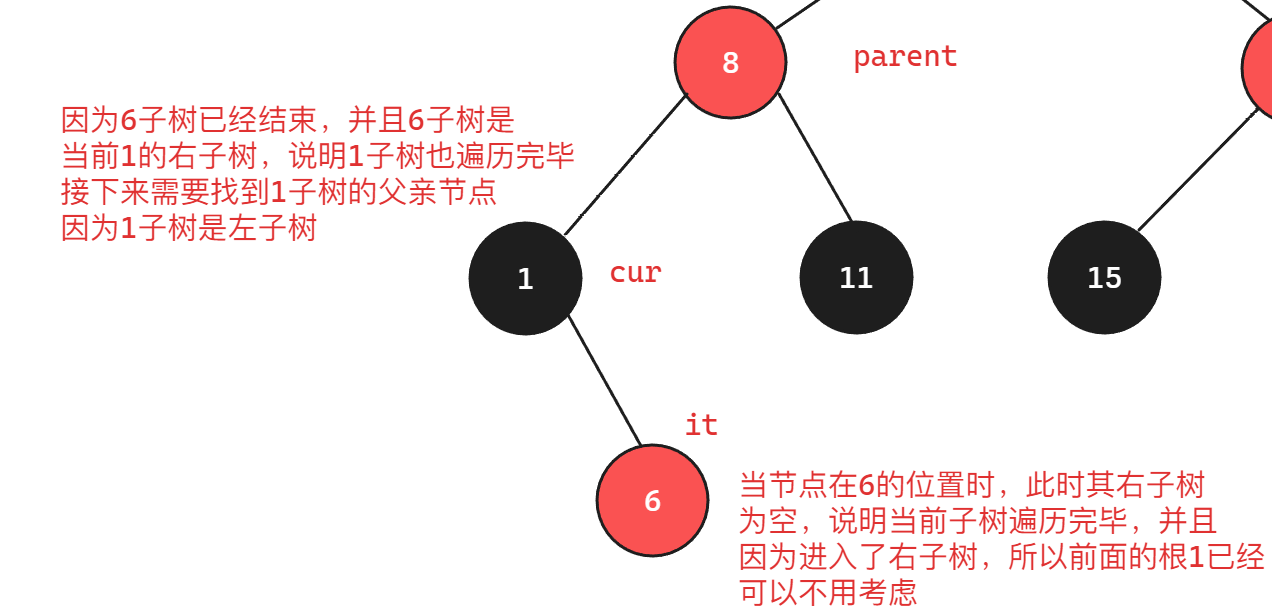
C++
// operator++()
RBTree_iterator operator++()
{
    if (_node->right)
    {
        node* leftMost = _node->_right;
        while (leftMost->_left)
        {
            leftMost = leftMost->_left;
        }

        // 找到后走到最左节点的位置
        _node = leftMost;
    }
    else
    {
        // 初始位置为迭代器位置
        node* cur = _node;
        // 记录当前节点parent的位置
        node* parent = cur->_parent;
        // 右子树结束则结束
        while (parent && cur == parent->_right)
        {
            cur = parent;
            parent = cur->_parent;
        }

        _node = parent;
    }

    return *this;
}

`operator--()`设计¶

设计operator--()的思路与operator++()思路基本相反，首先因为正向遍历的中序顺序是左子树->根->右子树，所以反向遍历的中序顺序是右子树->根->左子树，以当前节点为根节点看待当前子树时，其右子树的值就可以忽略，因为已经越过了右子树，所以反向遍历主要看左子树是否为空，如果左子树不为空，则找其最右节点；如果左子树为空，则代表当前子树已经结束，找到该子树的父亲，如果该子树依旧是其父亲的左子树，那么继续找到父亲的父亲，如此往复直到遇到空。但是需要注意的是，如果当前节点为end()的位置，那么需要进行一次特殊处理，将当前节点更新为整棵树的最右节点

Note

此处涉及到遍历整棵树，所以需要传递整棵树的根节点，需要对迭代器进行改动，新增一个_root成员，在Begin()和End()处传递整棵树的根

C++
// 迭代器修改
// 迭代器
iterator Begin()
{
    // 找到最左节点
    // ...

    // 返回最左节点作为起始位置以及根节点
    return iterator(leftMost, _root);
}

iterator End()
{
    return iterator(nullptr, _root);
}

// operator--()
RBTree_iterator operator--()
{
    if (_node == nullptr)// 特殊处理end()
    {
        node* rightMost = _root;
        while (rightMost && rightMost->_right)
        {
            rightMost = rightMost->_right;
        }

        _node = rightMost;
    }
    else if (_node->_left)
    {
        node* rightMost = _node->_left;
        while (rightMost->_right)
        {
            rightMost = rightMost->_right;
        }

        _node = rightMost;
    }
    else
    {
        node* cur = _node;
        node* parent = cur->_parent;
        while (parent && cur == parent->_left)
        {
            cur = parent;
            parent = cur->_parent;
        }

        _node = parent;
    }

    return *this;
}

map和set常规迭代器封装¶

因为红黑树中实现了begin()和end()，所以对于map和set来说，直接封装即可

首先在红黑树中声明迭代器

C++
typedef RBTree_iterator<V> Iterator;

接着在map和set中声明迭代器

C++
// set
typedef typename RBTree<T, T, setKeyOfT>::Iterator iterator;

// map
typedef typename RBTree<Key, pair<Key, T>, mapKeyOfV>::Iterator iterator;

最后封装红黑树中的迭代器

C++
// map和set迭代器
iterator begin()
{
    return rb_t.Begin();// 使用红黑树的迭代器
}

iterator end()
{
    return rb_t.End();
}

map和set的`const`迭代器设计¶

在前面设计常规迭代器时，对于set来说不能支持修改，所以常规迭代器也需要const进行修饰，但是不考虑对常规迭代器直接使用const版本的迭代器，而是在传递模版参数时直接使用const版本的参数

首先将引用和指针返回类型定义为迭代器模版参数Ref和Ptr，便于控制非const和const版本

C++
template <class V, class Ptr, class Ref>
struct RBTree_iterator

在红黑树的结构中定义迭代器，传递引用和指针

C++
typedef RBTree_iterator<V, V*, V&> Iterator;// 常规迭代器

typedef RBTree_iterator<V, const V*, const V&> constIterator;// const迭代器

设计const的Begin()和End()

C++
// const迭代器
constIterator Begin() const
{
    // 找到最左节点
    node* leftMost = _root;
    while (leftMost && leftMost->_left)
    {
        leftMost = leftMost->_left;
    }

    // 返回最左节点作为起始位置
    return Iterator(leftMost, _root);
}

constIterator End() const
{
    return Iterator(nullptr, _root);
}

在map和set中封装

C++
// set中声明const迭代器
typedef typename RBTree<T, T, setKeyOfT>::constIterator const_iterator;
// map中声明const迭代器
typedef typename RBTree<Key, pair<Key, T>, mapKeyOfV>::constIterator const_iterator;

// map和set中的const迭代器
const_iterator begin() const
{
    return rb_t.Begin();
}

const_iterator end() const
{
    return rb_t.End();
}

为了避免修改已经插入的内容，可以在模版参数中对指定类型声明为const类型

C++
// map-声明Key为const类型
RBTree<Key, pair<const Key, T>, mapKeyOfV> rb_t;

// set-声明Key为const类型
RBTree<T, const T, setKeyOfT> rb_t;

// 修改对应迭代器
typedef typename RBTree<T, const T, setKeyOfT>::Iterator iterator;
typedef typename RBTree<Key, pair<const Key, T>, mapKeyOfV>::constIterator const_iterator;

map和set的`insert()`函数¶

因为红黑树结构已经实现了insert()函数，所以对应map和set来说可以直接复用红黑树中的insert()函数，需要注意这里的insert()函数的返回值需要设计成pair<iterator, bool>类型，对于set来说没有影响，但是对于map来说，后面需要重载operator[]，所以使用该返回类型

C++
// 树插入
pair<Iterator, bool> insertNode(const V& data)
{
    // 创建仿函数对象获取内容
    KeyOfV kov;
    // 判断根节点是否为空，为空则作为第一个节点
    if (_root == nullptr)
    {
        _root = new node(data);
        return make_pair(Iterator(_root), true);
    }
    // 根节点不为空时接着遍历插入
    node* cur = _root;
    // 定义父亲节点记录父亲的位置
    node* parent = _root;
    while (cur)
    {
        if (kov(data) > kov(cur->_data))
        {
            // 大于根节点数据，插入在右子树，走到左子树的空位置
            parent = cur;
            cur = cur->_right;
        }
        else if (kov(data) < kov(cur->_data))
        {
            // 小于根节点数据，插入在左子树，走到右子树的空位置
            parent = cur;
            cur = cur->_left;
        }
        else
        {
            // 查到相等返回false
            return make_pair(Iterator(cur), false);
        }
    }

    // 创建node节点
    // 创建节点可以使用新节点，但是要使cur走到新节点的位置，便于下面判断新节点的平衡因子，再通过cur判断祖先节点的平衡因子
    cur = new node(data);
    // 记录新增点便于返回
    node* newNode = cur;

    // parent为叶子节点，链接新节点
    if (kov(parent->_data) < kov(data))
    {
        // 如果是右子树，则插入在右子树
        parent->_right = cur;
    }
    else
    {
        // 否则插入在左子树
        parent->_left = cur;
    }

    // 链接父亲
    cur->_parent = parent;
    // 插入节点颜色为红色
    cur->_col = Red;

    // 存在父亲且当父亲节点为红色时需要判断是否更新
    while (parent && parent->_parent && parent->_col == Red)
    {
        node* grandfather = parent->_parent;
        if (grandfather->_right == parent)
        {
            node* uncle = grandfather->_left;
            if (uncle && uncle->_col == Red)
            {
                // 叔叔存在且为红
                uncle->_col = parent->_col = Black;
                grandfather->_col = Red;

                cur = grandfather;
                parent = cur->_parent;
            }
            else
            {
                // cur在parent的右孩子
                if (cur == parent->_right)
                {
                    // 右右->左单旋
                    rotateLeft(grandfather);
                    // 改变颜色
                    grandfather->_col = Red;
                    parent->_col = Black;
                }
                else
                {
                    // 右左->右左双旋
                    rotateRight(parent);
                    rotateLeft(grandfather);

                    cur->_col = Black;
                    grandfather->_col = Red;
                }
                // 旋转结束后不需要再向上更新
                break;
            }
        }
        else
        {
            node* uncle = grandfather->_right;
            if (uncle && uncle->_col == Red)
            {
                // 叔叔存在且为红
                uncle->_col = parent->_col = Black;
                grandfather->_col = Red;

                // 继续向上更新
                cur = grandfather;
                parent = cur->_parent;
            }
            else
            {
                if(cur == parent->_left)
                {
                    // 叔叔不存在
                    // 左左->右单旋
                    rotateRight(grandfather);
                    // 改变颜色
                    grandfather->_col = Red;
                    parent->_col = Black;
                }
                else
                {
                    // 左右->左右双旋
                    rotateLeft(parent);
                    rotateRight(grandfather);

                    // 改变颜色
                    grandfather->_col = Red;
                    cur->_col = Black;
                }
                // 旋转结束后不需要再向上更新
                break;
            }
        }
    }

    // 根节点为黑色
    _root->_col = Black;

    return make_pair(Iterator(newNode), true);
}

map和set封装红黑树的insert()函数

C++
// set中的insert()函数
pair<iterator, bool> insert(const T& key)
{
    return rb_t.insertNode(key);
}

// map中的insert()函数
pair<iterator, bool> insert(const pair<const Key, T>& kv)
{
    return rb_t.insertNode(kv);
}

map中的`operator[]`¶

因为map中的operator[]函数有插入+修改的功能，所以内部需要调用insert()函数，当插入失败时，返回已经存在节点的迭代器的second即为对应节点的value值，插入成功时，返回成功插入的节点的迭代器的second即为对应节点的value值

C++
// 重载operator[]
T& operator[](const Key& key)
{
    pair<iterator, bool> ret = insert(make_pair(Key, T()));
    return ret.first->second;
}

map和set类模拟实现¶

map和set模拟实现介绍¶

map和set类定义¶

map和set类的遍历比较规则设计¶

map和set中的常规迭代器设计¶

常规迭代器结构定义¶

operator*()设计¶

operator->()设计¶

operator!=()设计¶

operator==()设计¶

operator++()设计¶

operator--()设计¶